Ling Chen, Bolun Chen, Yixin Chen
Отдел компьютерных наук, Университет Янчжоу, Янчжоу, Китайская государственная ключевая лаборатория Novel Software Tech, Нанкинский университет, Нанкин, Китайский отдел компьютерных наук, Вашингтонский университет в Сент-Луисе, США
Выбор функции изображения (FS) - важная задача, которая может повлиять на эффективность классификации и распознавания изображений. В этой статье мы представляем алгоритм выбора признаков, основанный на оптимизации колонии муравьев (ACO). Для n функций большинство методов выбора объектов на основе ACO используют полный граф с ребрами O (n2). Однако искусственные муравьи в предлагаемом алгоритме пересекаются на орграфе с только 2n дугами. Алгоритм использует производительность классификатора и количество выбранных функций как эвристическую информацию и выбирает оптимальное подмножество функций с точки зрения размера набора функций и эффективности классификации. Экспериментальные результаты на разных изображениях показывают, что наш алгоритм может получить лучшую точность классификации с меньшим набором функций по сравнению с другими алгоритмами
Ключевые слова: оптимизация колонии муравьев; уменьшение размерности; выбор функции; классификация изображений
Уменьшение размерности шаблона с помощью извлечения функции является одной из наиболее важных задач распознавания и классификации. Выбор функций имеет большое значение в таких областях, как биоинформатика [1], обработка сигналов [2], обработка изображений [3], категоризация текста [4], интеллектуальный анализ [5], распознавание образов [6], медицинская диагностика [7], распознавание изображений с помощью дистанционного датчика [8]. Цель выбора функции - выбрать подмножество доступных функций, исключив ненужные функции. Чтобы извлечь как можно больше информации из заданного набора изображений при использовании наименьшего числа функций, мы должны устранить функции с небольшой или никакой прогностической информацией и игнорировать избыточные функции, которые сильно коррелированы.
Многие алгоритмы выбора функций включают эвристические или случайные стратегии поиска, чтобы сократить время вычислений. Для большого количества функций эвристический поиск часто используется для поиска лучшего подмножества функций. Однако точность результатов классификации с помощью подмножества конечных признаков часто уменьшается [6]. В последнее время для выбора функций используются алгоритмы, основанные на природе. Были предложены алгоритмы оптимизации на основе популяции для выбора функций, такие как генетический алгоритм (GA) [3,9], оптимизация колонии муравьев (ACO) [1,4], оптимизация частиц (PSO) [10]. Эти методы - это методы стохастической оптимизации, направленные на достижение лучших решений путем ссылки на обратную связь и эвристическую информацию.
Оптимизация колонии муравьев (ACO) - алгоритм эволюционного моделирования, предложенный M. Dorigo. [11]. Он успешно используется для обнаружения системных сбоев, планирования рабочих мест, балансировки сетевой нагрузки, раскраски графов, робототехники и других проблем оптимизации комбинаций.
В этой статье мы представляем алгоритм выбора функций ACO, ACOFS, чтобы уменьшить потребность в памяти и время вычисления. В этом алгоритме искусственные муравьи пересекаются на орграфе с только 2n дугами. Алгоритм использует производительность классификатора и количество выбранных функций как эвристическую информацию и выбирает оптимальное подмножество функций с точки зрения размера набора функций и производительности классификатора. Экспериментальные результаты на наборах данных изображений показывают, что предлагаемый алгоритм обладает превосходной производительностью. Сравнивая с другими существующими алгоритмами, наш алгоритм может получить лучшую точность классификации с меньшим набором функций из изображений.
Учитывая набор функций n, задача выбора функции состоит в том, чтобы найти минимальное подмножество элементов размера s (s < n), сохраняя при этом довольно высокую точность классификации при представлении исходных функций. Большинство алгоритмов, основанных на ACO для выбора функций, использует полный график, на котором муравьи пытаются построить путь с частью узлов. Поскольку решение выбора функции является подмножеством этих выбранных функций, среди компонентов решения нет никакого упорядочения. Для представления такого решения нет необходимости использовать путь в полном графике. В ACO на таком полном графике муравей на одном узле (функция) выбирает ребро, соединяющее другой узел (функцию) на основе феромона и эвристическую информацию, назначаемую на этом краю между двумя узлами (функциями). Но в задаче выбора функции одна функция, которая будет выбрана, не зависит от последней функции, добавленной к частичному решению. Поэтому нет необходимости использовать полный граф с ребрами O (n2) в алгоритме ACO.
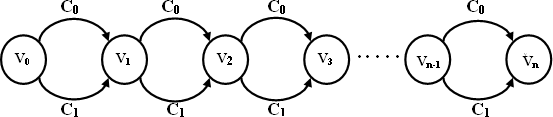
Чтобы эффективно применять алгоритм ACO для выбора функции, мы должны переопределить способ использования графа представления. Мы предложили алгоритм оптимизации алгоритма на дискретном пространстве поиска, представленный орграфом, только с дугами O (n), как показано на рисунке 1, где узлы представляют собой объекты, а дуги, соединяющие два соседних узла, указывающие выбор следующей функции.

Обозначим n функций как f1, f2, ..., fn, i-й узел vi используется для представления функции fi. Дополнительный узел v0 помещается в начале графика, где каждый муравей начинает свой поиск. Как показано на рисунке 1, муравьи перемещаются на орграфе от v0 до v1, а затем до v2 и т. Д. Муравей завершает свой тур и выводит это подмножество этой функции, когда он достигает последнего узла vn. Когда муравей завершает поиск с v0 на vn, дуги на его трассе образуют решение
Поиск оптимального подмножества объектов - это процедура прохождения муравьев по графику. Предположим, что муравей сейчас находится в узле vi-1 и ему нужно выбрать один путь, соединяющий vi для прохождения. Вероятностная функция перехода, обозначающая вероятность появления муравья в узле vi-1 для выбора пути j для достижения vi сочетая эвристическую желательность и плотность феромонов дуги. Вероятность муравья в узле vi-1 для выбора дуги j в момент времени t:
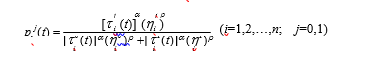
Из (1) видно, что вероятность перехода, используемая ACO, зависит от интенсивности феромона j (t) и эвристической информации j. Для эффективного баланса влияния информации положительной обратной связи от предыдущих высококачественных решений ижелательность дуги, мы должны выбрать правильные значения параметров ? и ?. Когда ? = 0, информация о положительной обратной связи не используется. Поскольку предыдущий опыт поиска теряется, поиск ухудшается до стохастического жадного поиска. Когда ? = 0, потенциальным преимуществом дуг пренебрегают, и он становится полностью случайным поиском.
Эвристическая информация n1 - это желательность выбора дуги j между узлами vi-1 и vi, что означает предпочтение муравья выбирать функцию fi. Существует множество способов определения подходящего значения n1. Это может быть любая функция оценки способности распознавания функции fi, такая как приблизительная мера зависимости или измерение на основе энтропии. Мы устанавливаем значение 1, используя F-score, что является простым измерением для оценки способности распознавания функции fi, определяемой следующим образом:
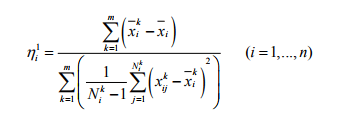
Здесь m - количество классов набора изображений; n - количество функций; k - число выборок функции fi-класса k, (k = 1,2, ..., m, i = 1,2, ..., n), x является j-м обучающим образцом для функции fi изображений в классе k, (j = 1,2, ..., N k), xi - среднее значение функции fi всех изображений, xi - среднее значение функции fi изображений в классе k.
В (2) числитель указывает на дискриминацию между классами набора изображений, а знаменатель определяет дискриминацию внутри каждого класса. Более крупное значение 1 означает, что функция fi обладает большей дискриминационной способностью.
В методе оптимизации на основе ACO критически важна разработка стратегии обновления феромонов и измерение качества решений.
На каждой итерации алгоритм ACOFS обновляет значение феромонов на каждой дуге в соответствии с феромоном и эвристической информацией о дуге.
Очевидно, что, если муравьев выбирает дугу c j, феромону на этой дуге должно быть назначено большее приращение, и муравьи должны выбрать дугу j с большей вероятностью в следующей итерации. Это создает положительную обратную связь системы феромонов. На каждой итерации феромон на каждой дуге обновляется согласно формулам (3), (4) и (5).
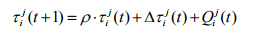
где
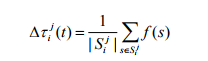
и
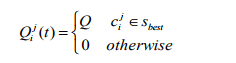
В (4) s j - множество решений, порожденных на t-й итерации, проходящей через c j. В (5) Sbest - лучшее решение, найденное до сих пор, а Q - положительная константа. Чтобы подчеркнуть влияние наилучшего решения, добавим дополнительный прирост феромонов на дугах, включенных в Sbest.
На основе решения муравья, которое является выбранным подмножеством, качество решения с точки зрения точности классификации оценивается путем классификации наборов обучающих данных с использованием выбранных функций. Точность проверки измеряет количество примеров, которые были правильно классифицированы. Кроме того, количество функций в наборе также учитывается в функции качества. Подмножество с меньшими возможностями может получить более высокое качество функции. Функция качества f (s) решения s определяется следующим образом:
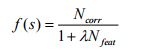
где Ncorr - количество примеров, которые правильно классифицированы, Nfeat - это количество функций, выбранных в s, ? - постоянная величина для корректировки важности точности и количества выбранных функций. Схема, получающая более высокую точность и с меньшими возможностями, получит большее значение функции качества.
Чтобы проверить эффективность и эффективность предложенного алгоритма выбора ACOFS, мы проверим его на основе серии экспериментов. Все эксперименты выполнялись на Pentium IV, Windows XP, P1.7G, используя VC ++ 6. 0, и результаты визуализируются на Matlab 6.0
Набор изображений был протестирован, чтобы продемонстрировать классификационную точность и определить, может ли предлагаемый алгоритм правильно выбирать соответствующие функции. Набор данных содержит 80 изображений в 4 классах. Набор данных содержит 19 функций, включая первый и второй порядковый момент, центральный момент первого и второго порядка, степень твиста, пиковые значения, энтропию моментов и статистическую статистику серого дифференцирования, такую как контраст, угол второго порядка (ASM), среднее значение, энтропия и т.д.
В наборе изображений алгоритм ACFS применяется для выбора соответствующих функций и сравнивается с GA GA на основе GA [21] и модифицированным алгоритмом ACO для выбора функции, представленным в [26], который обозначается как mACO.
Для GA-набора функций GA, мы устанавливаем длину хромосом как количество функций. В хромосоме каждый ген gi соответствует i-й функции. Если gi = 1, это означает, что мы выбираем i-й элемент. В противном случае gi = 0, что означает, что i-я функция игнорируется. Итерациями по производству хромосом для нового поколения, кроссовера и мутаций алгоритм пытается найти хромосому с наименьшим числом 1, а точность классификатора максимизируется. Чтобы выбрать людей для следующего поколения, использовался метод выбора колес рулетки GA. Мы устанавливаем параметры GA как: вероятности кроссовера и мутации Pcroos = 0,9 и Pmutation = 0,25, размер популяции m = 50, а максимальные итерации k = 50.
Для ACO-алгоритмов ACOFS и mACO мы применили их с тем же размером популяции, что и GA GA. Различные параметры, приводящие к лучшей конвергенции, тестируются, и лучшие параметры, которые получают путем моделирования, следующие: ? = 1, ? = 0,5, скорость испарения ? = 0,951, начальная интенсивность феромонов каждой дуги равна 1, число of ant в каждой итерации m = 50 и максимальных итерациях k = 50. Эти значения выбираются так, чтобы оправдывать сравнение с GA. Для каждого подмножества полученных характеристик его качество измеряется путем классификации наборов обучающих образов с использованием классификатора SVM. Для оценки эффективности учитывается количество выбранных функций и качество результатов классификации.
Чтобы оценить среднюю точность классификации выбранных подмножеств, используется 10-кратная и 5-кратная перекрестная проверка (CV). Для трех алгоритмов вычисляется и записывается точность CV по данным обучения и тестирования наилучшего решения на каждой итерации.
В таблице 1 показано количество функций, выбранных в наилучшем решении, полученном тремя алгоритмами. Из таблицы видно, что ACOFS выбирает наименьшее количество функций, сохраняя при этом высокую точность классификации.

Мы измеряем качество результатов классификации в двух критериях, а именно: отзыв и точность каждого класса. Среднее значение и точность классификации i-го класса определяются следующим образом

Здесь Nc (i) - количество изображений в i-м классе, NTP (i) - количество изображений, правильно классифицированных в i-й класс, NFP (i) - количество изображений, неправильно классифицированных в i-й класс.
Из таблиц видно, что предлагаемый алгоритм ACOFS имеет лучшую точность, чем алгоритмы mACO, GA. Даже используя меньше функций, алгоритм ACOFS по-прежнему может получить более высокую точность, чем алгоритмы mACO, GA. Например, в 5-кратном CV-тестировании на наборах тестов средняя точность ACOFS составляет 95%, тогда как для GA и 88,55%, а для mACO - 87,5%. Это означает, что точность результатов ACOFS всегда лучше, чем точность алгоритмов mACO и GAs
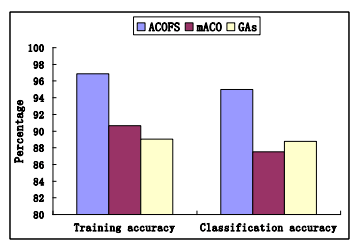
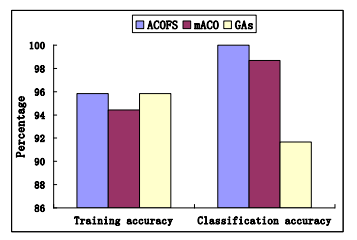
Persantage - проценты; traning accuracy - точность обучения; classification accuracy - точность классификации
Сравнение среднего значения и точности трех алгоритмов показано на рис. 2 и 3 соответственно. Из рисунков и таблиц можно заключить, что предлагаемый алгоритм ACOFS может успешно выбрать подмножество признаков, которые могут получить высокую точность классификации. По сравнению с алгоритмами GA и mACO в тестах с использованием одного и того же набора изображений ACOFS может получить лучшую точность классификации, но имеет меньший набор функций.
Мы предложили алгоритм ACOFS, основанный на ACO. Алгоритм использует производительность классификатора и количество выбранных функций как эвристическую информацию и выбирает оптимальное подмножество функций с точки зрения наименьшего номера функции и лучшей производительности классификатора. Экспериментальные результаты на наборах данных изображений показывают, что алгоритм ACOFS может получить лучшую точность классификации, но имеет меньший набор функций, чем другие аналогичные методы.