Аннотация
В статье описывается относительно простой, но мощный и универсальный метод прогнозирования данных временных рядов – простое экспоненциальное сглаживание. Простое экспоненциальное сглаживание (SES) – это метод краткосрочного прогнозирования, который предполагает разумно стабильное среднее значение в данных без тренда (последовательный рост или снижение). Это один из самых популярных методов прогнозирования, который использует взвешенную скользящую среднюю прошлых данных в качестве основы для прогноза. Эта процедура дает больший вес более поздним наблюдениям и меньшему весу наблюдений в более отдаленном прошлом. Точность метода SES сильно зависит от оптимального значения константы сглаживания a. Для определения оптимального значения в документе использовался традиционный метод оптимизации, основанный на средней абсолютной ошибке (MAE), средней абсолютной процентной погрешности (MAPE) и квадратный корень из среднеквадратичной ошибки (RMSE).
Ключевые слова:временные ряды, простая экспоненциальная сглаживающая модель, прогноз, сглаживающая константа, среднеквадратичная ошибка.
1. Введение
Временной ряд представляет собой последовательность наблюдений, индексированных по времени, обычно упорядоченных в равноотстоящих интервалах и коррелированных. В наши дни хорошо известно важность исследований временных рядов. В этих исследованиях приводятся показатели экономики страны, уровень безработицы, экспортные и импортные тарифы и т.д. Самая интересная и амбициозная задача анализа временных рядов – прогнозирование будущих значений. Обычно строятся модели для прогнозирования будущих значений временного ряда [4].
Метод экспоненциального сглаживания – наиболее широко используемый метод прогнозирования. Формулировка метода экспоненциального сглаживания возникла в 1950–х годах из оригинальной работы Брауна (1959, [2]) и Холта (1957, [6]), которые работали над созданием моделей прогнозирования для систем управления запасами.
Экспоненциальное сглаживание – это интуитивный метод прогнозирования, который взвешивает наблюдаемые временные ряды неравномерно. Последние наблюдения взвешиваются более интенсивно, чем отдаленные наблюдения. Неравномерность взвешивания выполняется с использованием одного или нескольких параметров сглаживания, которые определяют, сколько веса дано каждому наблюдению [9].
Простейший метод такого типа, простое экспоненциальное сглаживание (SES), подходит для серии, которая перемещается случайным образом выше и ниже постоянного среднего (стационарный ряд). Он не имеет тенденции и не имеет сезонных моделей [16].
Метод Holt–Winters, также называемый двойным экспоненциальным сглаживанием, является расширением экспоненциального сглаживания, предназначенного для трендовых и сезонных временных рядов. Сглаживание Holt–Winters является широко используемым инструментом для прогнозирования бизнес–данных, которые содержат сезонность, изменяющиеся тенденции и сезонную корреляцию [5].
Модель экспоненциального сглаживания является широко используемым методом анализа временных рядов. Эта популярность может быть объяснена его простотой, вычислительной эффективностью, простотой корректировки ее реагирования на изменения в прогнозируемом процессе и ее разумной точностью [11].
Как правило, экспоненциальное сглаживание рассматривается как недорогой метод, который дает хороший прогноз в самых разных приложениях. Кроме того, требования к хранению и вычислению данных минимальны, что делает экспоненциальное сглаживание подходящим для приложений реального времени.
2. Простая модель экспоненциального сглаживания
Простая модель экспоненциального сглаживания (SES) обычно основана на предположении, что уровень временных рядов должен колебаться примерно на постоянном уровне или медленно меняться за время [9].
2.1. Математическая формулировка
Модель SES задается уравнением (рис.1):
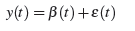
Рисунок 1 – Уравнение модели экспоненциального сглаживания
Где B(t) принимает постоянную в момент времени t и может медленно изменяться за время; E(t) является случайной величиной и используется для описания эффекта стохастической флуктуации.
Пусть наблюдаемый временной ряд равен y1, y2,..., yn. В любом случае, в этой простой модели, предсказать yt это просто предсказать (оценить) В. Для оценки, имеет смысл использовать все прошлые наблюдения, но из–за уменьшения корреляции, когда вы возвращаетесь в прошлое, к более старым наблюдениям.
Формально простое уравнение экспоненциального сглаживания принимает вид (рис. 2):

Рисунок 2 – Простое уравнение экспоненциального сглаживания
Где yt – фактическое, известное значение ряда за время t; Ft – прогнозируемое значение переменной Y в момент времени t; Ft + 1 – прогнозируемое значение в момент времени t +1; a – сглаживающая константа [3].
Прогноз Ft + 1 основан на взвешивании последних наблюдение yt с весом a и весом самого последнего прогноз Ft с весом 1–a.
Чтобы начать работу с алгоритмом, нам нужен первоначальный прогноз, фактическое значение и константа сглаживания.
Поскольку F1 неизвестно, мы можем:
- установить первую оценку, равную первому наблюдению, далее будем использовать F1 = y1;
- используйте среднее значение первых нескольких наблюдений ряда данных для начального сглаженного значения.
Константа сглаживания a – это выбранное число между 0 и 1. Переписывая модель (рис.2), мы можем видеть одно из представлений о модели SES:  изменение прогнозируемого значения пропорционально ошибке прогноза. То есть
изменение прогнозируемого значения пропорционально ошибке прогноза. То есть  где остаточные
где остаточные  это ошибка прогноза в момент времени t.
это ошибка прогноза в момент времени t.
Таким образом, прогноз экспоненциального сглаживания – это старый прогноз плюс корректировка ошибки, которая произошла в последнем прогнозе [1, 12].
Итерируя формулу простого уравнения экспоненциального сглаживания (рис.3), получим уравнение прогноза в общем виде (рис.4).
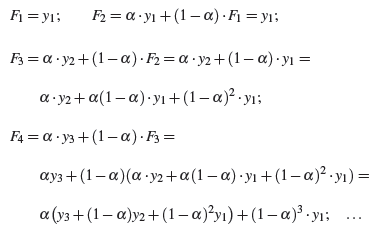
Рисунок 3 – Итерация формулы

Рисунок 4 – Уравнение прогноза в общем виде
Где Ft + 1 – прогнозируемое значение переменной Y в момент времени t+1 от фактических значений ряда yt, yt–1, yt–2 и так далее в прошлое к первому известному значению временного ряда, y1 [3, 13].
Следовательно, Ft + 1 – взвешенное скользящее среднее всех прошлые наблюдения.
Серия весов, используемых при составлении прогноза Ft + 1 является (рис.5):
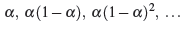
Рисунок 5 – Серия весов, используемых при составлении прогноза Ft + 1
Из рисунка 5 очевидно, что веса экспоненциальные; следовательно это экспоненциально взвешенное скользящее среднее [1]. Экспоненциальное уменьшение весов до нуля очевидно. Это показано на рисунке 6. Распад медленнее при малых значениях а, поэтому мы можем контролировать скорость распада, выбирая соответствующее а.
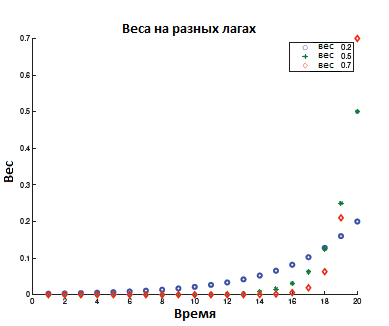
Рисунок 6 – Экспоненциально уменьшающиеся веса
2.2. Измерение ошибки прогноза
После указанной модели ее характеристики производительности должны быть проверены или подтверждены путем сопоставления его прогноза с историческими данными для процесса, который он был разработан для прогнозирования.
Это не является консенсусом среди исследователей о том, какая мера лучше всего подходит для определения наиболее подходящего метода прогнозирования. Точность – это критерий, который определяет наилучший метод прогнозирования; таким образом, точность является самой важной задачей при оценке качества прогноза. Целью прогноза является минимизация ошибки [14].
Некоторые общие индикаторы, используемые для оценки точности, это MAE (средняя абсолютная ошибка), MSE (среднеквадратичная ошибка), RMSE (квадратный корень из среднеквадратичной ошибки) или MAPE (средняя абсолютная ошибка в процентах) (рис.7):

Рисунок 7 – Формулы для оценок ошибки прогнозирования временных рядов
Где yt – фактическое значение за время t; et – остаточный момент времени t; n – общее число периодов времени.
Cредняя абсолютная ошибка(MAE) – это мера общей точности, которая дает указание на степень распространения, где всем ошибкам присваивается одинаковый вес. Если метод подходит к данным прошлых временных рядов очень хорошо, MAE близка к нулю, тогда как если метод плохо соответствует данным прошлых временных рядов, MAE велика. Таким образом, когда сравниваются два или более метода прогнозирования, можно выбрать наиболее подходящий вариант с минимальной МАE [14].
MSE также является мерой общей точности, которая дает указание на степень распространения, но здесь большие ошибки дают дополнительный вес. Это общепринятый метод оценки экспоненциального сглаживания и других методов [7].
Часто рассматривается квадратный корень MSE, RMSE, поскольку серьезность ошибки прогноза затем обозначается в тех же измерениях, что и фактические и прогнозные значения.
MAPE является относительной мерой, которая соответствует MAE. Это самая полезная мера для сравнения точности прогнозов между различными товарами или продуктами, поскольку она измеряет относительную производительность. Это одна мера точности, обычно используемая в количественных методах прогнозирования [10]. Если расчетное значение MAPE составляет менее 10%, оно интерпретируется как отличное точное прогнозирование, между 10–20% хорошее прогнозирование, приемлемое прогнозирование между 20–50% и более чем 50% это уже неточное прогнозирование [8].
Выбор показателя ошибки оказывает важное влияние на выводы о том, какой из методов прогнозирования является наиболее точным.
2.3 Выбор оптимального значения для константы сглаживания
Точность прогнозирования метода SES зависит от постоянной сглаживания. Выбор подходящего значения экспоненциальной сглаживающей константы очень важен, чтобы минимизировать ошибку в прогнозировании.
Выбор константы сглаживания в основном зависит от суждения или проб и ошибок, используя ошибки прогноза для принятия решения. Цель состоит в том, чтобы выбрать константу сглаживания, которая уравновешивает преимущества сглаживания случайных вариаций с учетом преимуществ реагирования на реальные изменения когда они происходят.
Константа сглаживания служит весовым коэффициентом. Когда a близок к 1, новый прогноз будет содержать существенную корректировку для любой ошибки, которая произошла в предыдущем прогнозе. Когда a близок к 0, новый прогноз очень похож на старый прогноз. Константа сглаживания a не является произвольным выбором, но обычно находится между 0,1 и 0,5. Низкие значения a используются, когда средний уровень имеет тенденцию быть стабильным; более высокие значения используются, когда базовое среднее восприимчиво к изменению.
На практике константа сглаживания часто выбирается сетным поиском пространства параметров; т.е. различные решения для a пробуждаются, например, с a = 0: 1 до a = 0: 9 с приращениями 0,1 [1, 12]. Значение a с наименьшим значением MAE, MSE, RMSE или MAPE выбрано для использования при составлении будущих прогнозов.
Выводы
Экспоненциальное сглаживание это представление о том, что самые последние наблюдения обычно дают лучшее руководство для будущего, поэтому мы хотим иметь весовую схему с уменьшающимися весами для более старых наблюдений. Выбор константы сглаживания важен при определении рабочих характеристик экспоненциального сглаживания. Чем меньше значение a, тем медленнее ответ. Большие значения причина, по которой сглаженное значение реагируют быстро – не только на реальные изменения, но и на случайные колебания [11]. Простая модель экспоненциального сглаживания хороша только для несезонных моделей с нулевым трендом и краткосрочным прогнозом, потому что, если мы продолжим следующий период, прогнозируемое значение для этого периода должно использоваться в качестве суррогата для фактического спроса на любой прогноз на следующий период. Следовательно, нет возможности добавлять корректирующую информацию (фактический спрос), и любая ошибка растет экспоненциально.
Список использованной литературы
- ACZEL, A. D.: Complete Business Statistics, Irwin, 1989, ISBN 0–256–05710–8.
- BROWN, R. G.: Statistical Forecasting for Inventory Control, McGraw–Hill: New York, 1959.
- BROWN, R. G. – MEYER, R. F.: The Fundamental Theory of Exponential Smoothing, Operations Research, 9, 673–685, 1961.
- CORDEIRO, C. – NEVES, M. M.: Bootstrap and Exponential Smoothing Working together in Forecasting Time Series, Proceedings in Computational Statistics, Physica–Verlag, 891–899, 2008.
- GELPER, S. – FRIED, R. – CROUX, CH.: Robust Forecasting with Exponential and Holt Winters Smoothing, Journal of forecasting, Vol. 29, No. 3, 285–300, 2010.
- HOLT, C. C.: Forecasting trends and seasonals by exponentially weighted averages, O.N.R. Memorandum 52/1957, Carnegie Institute of Technology, 1957.
- JARETT, J.: Business Forecasting Methods, Cambridge, MA: Basil Blackwell, 1991.
- LEWIS, C. D.: Industrial and Business Forecasting Methods, London, Butterworths, 1982.
- LI, Z. P. – YU, H. – LIU, Y. C. – LIU, F. Q.: An Improved Adaptive Exponential Smoothing Model for Short Term Travel Time Forecasting of Urban Arterial Street, Acta automatica sinica, Vol. 34, No. 11, 1404– 1409, 2008.
- MAKRIDAKIS, S. – WHEELWRIGHT, S. C. – HYNDMAN, R. J.: Forecasting Methods and Applications, New York, Wiley, 1998.
- MONTGOMERY, D. C. – JOHNSON, L. A. – GARDINER, J. S.: Forecasting and Time Series Analysis, McGraw–Hill, Inc., 1990, ISBN 0–07–042858–1.
- OSTERTAGOVA, E.: Applied Statistics, [in Slovak], Elfa, Kosice, 2011, ISBN 978–80–8086–171–1.
- OSTERTAGOVA, E. – OSTERTAG, O.: The Simple Exponential Smoothing Model, Proceedings of the 4th International Conference on Modelling of Mechanical and Mechatronic Systems, Technical University of Kosice, Slovak Republic, 380–384, 2011.
- RYU, K. – SANCHEZ, A.: The Evaluation of Forecasting Methods at an Institutional Foodservice Dining Facility, The Journal of Hospitality Financial Management, Vol. 11, No. 1, 2003.
- SANJOY, K. P.: Determination of Exponential Smoothing Constant to Minimize Mean Square Error and Mean Absolute Deviation, Global journal of research in engineering, Vol. 11, 2011.
- YORUCU, V.: The Analysis of Forecasting Performance by Using Time Series Data for Two Mediterranean Island, Review of Social, Economic & Business Studies, Vol. 2, 175–196, 2003.