МЕТОДЫ КАЛИБРОВКИ ЦИФРОВЫХ КАМЕР

Фабио Ремондино, Институт геодезии и фотограмметрии, ETH Цюрих, Швейцария;

Клайв Фрейзер, Отдел геоматики, Университет Мельбурна, Австралия.

КЛЮЧЕВЫЕ СЛОВА: калибровка камеры, точность, масштабирование, искажение.

АНОТАЦИЯ

Калибровка камеры всегда была важным компонентом фотограмметрического измерения, при этом самокалибровка в настоящее время является интегральная и регулярно применяемая операция в рамках фотограмметрической триангуляции, особенно в высокоточных измерениях. С очень быстрым ростом внедрения готовых цифровых камер для множества 3D-измерительных программ, однако существует множество ситуаций, когда геометрия сети изображений не будет поддерживать надежное восстановление параметров камеры через калибровку на рабочем месте. По этой причине автономная калибровка камеры снова стала важным выпуском в ближней фотограмметрии, а также остается предметом исследовательской заинтересованности в компьютерном видении. В этой статье рассмотрены текущие подходы, принятые для калибровки камеры в ближней фотограмметрии, компьютерного зрения, и аспекты самокалибровки. Кроме того, суммируются результаты калибровки камеры с использованием разных алгоритмов. А также рассмотрено влияние хроматических аберраций при моделированных радиальных искажений это связано с тем, что по-прежнему существуют проблемы исследования в фотограмметрической калибровке цифровых камер потребительского класса.

1. ВВЕДЕНИЕ

Точная процедура калибровки и ориентации камеры необходима для извлечения точных и надежных данных 3D–метрической информация из изображений. Рассматривается калибровка камеры, если главное расстояние, смещение главной точки и параметры искажения объектива известны. Во многих программах, особенно в компьютерном зрении (CV), известно только фокусное расстояние в то время как для точных фотограмметрических измерений обычно используются все параметры калибровки. Различный алгоритмы калибровки камеры были зарегистрированы в фотограмметрии и CV–литературе. Алгоритмы обычно основаны на перспективных или проективных моделях камер, причем наиболее популярным подходом является самокалибровка которая была впервые введена в фотограмметрии в начале 1970–х годов. Аналитическая калибровка камеры была основной темой исследовательской заинтересованности в фотограмметрии в течение следующего десятилетия, хотя в условиях исследований сегодня привлекает меньше внимания.

Одна из возможных причин калибровки камеры является текущей «Горячей» темой исследования, безусловно, она заключается в том, что аналитическая самокалибровка во многих отношениях достигла зрелости в середине 1980–х годов. Самокалибровка вызывала интерес к исследованиям в первые дни цифровых камер, но можно сказать, что в середине 1990–х годов, автоматизированные системы метрологии (например, Ganci & Handley,1998) достигли высот. В таких системах параметры калибровки по существу рассматриваются как «параметры неудобства», которые необходимы, но не представляют большой интерес для них самих. Однако это недавно изменилось, поскольку применение цифровых камер потребительского класса для множества измерительных задач в геометрии сети не способствует самокалибровке. ним относятся, например, реконструкция аварий и некоторые проекты по регистрации наследия. В связи с этим возникает новый интерес к автономным подходам фотограмметрической калибровки, особенно к полностью автоматической калибровке. Камерная калибровка по–прежнему является областью активных исследований в сообществе CV, что, возможно, является неудачной характеристикой большей части работы, заключающейся в том, что она уделяет слишком мало внимания предыдущим результатам фотограмметрии. Часть этого вполне может быть объяснена с точки зрения отсутствия внимания аспектам точности и базовой предпосылки, что должно быть известно о камере, которая должна быть «откалибрована» в рамках линейного проективания, а не Реконструкция евклидовой сцены.

Многое можно сказать о продолжающемся искажении фотограмметрических подходов в литературе по CV как о сложной и не поддающейся полной автоматизации процессе обработке зум-объективов или нестабильной внутренней ориентации (IO) и т. д. Однако такие вопросы здесь не рассматриваются и авторы будут сосредоточены на методах калибровки камеры, которые имеют потенциал для практического применения. Во многих отношениях трудно всесторонне сравнить калибровочные подходы от двух общин, так как в каждом из них зрение может быть разным. В то время как фотограмметрическая калибровка может быть спроектирована так, чтобы поддерживать последующее измерение пространства объектов, требующее точности 1: 20 000, требование калибровки для структуры из программы движения может потребовать позиционирования точек объекта с точностью до, скажем, 5% расстояния между камерами и объектами. Основное внимание в этой статье будет уделяться подходам к калибровке, которые обеспечивают использование фотограмметрических программ даже на низком уровне точности.

Существует обширная литература по калибровке цифровых камеры с темами от общих обзоров (Fryer, 1996; Fraser, 2001) к общим исследованиям (Bösemannet al., 1990; Fraser & Shortis, 1995; Jantos et al., 2002), цифровые камеры (Kunii & Chikatsu, 2001; Läbe & Förstner, 2004; Cronk et al., 2006), стабильность параметров (Shortis 1997; Peipe & Stephani, 2003; Läbe & Förstner, 2004), поведение параметров IO (Wiley & Wong, 1995; Läbe &Förstner, 2004) и аспекты точности (D'Apuzzo & Maas, 1999; Salvi et al., 2002; Fraser & Al–Ajlouni, 2006). Для того, чтобы вспомнить и повторить основные, а иногда и забытые принципы калибровки камеры, теперь будут рассмотрены общие модели и методы, которые будут проверены на выбранных алгоритмах и проанализированы результаты.

2. МЕТОДЫ И МОДЕЛИ КАЛИБРОВКИ

В фотограмметрических терминах отклонения от коллинеарности могут быть смоделированы так, что основные уравнения перспективной проекции может применяться для процесса калибровки. Характер программ и требуемая точность могут диктовать, какая из двух основных базовых функциональных моделей должны быть приняты:

• Модель камеры, основанная на перспективной проекции, где подразумевается, что IO является стабильным (по крайней мере для данного фокального отклонения от коллинеарности, линейной и нелинейной. Эта модель на основе коллинеарности обычно требует пяти и более соответствий в сети с несколькими изображениями, из-за его нелинейного характера требуются аппроксимация значения параметров для настройки расслоения наименьших квадратов, которые восстанавливают параметры калибровки.

• Модель проективной камеры, поддерживающая проективные, а не реконструкцию евклидовой сцены. Такая модель, характеризующаяся по основным матрицам и фундаментальным матричным моделям, может учитывать переменные и неизвестные фокусные расстояния, но необходимо минимум 6-8 соответствий, чтобы облегчить линейное решение, которое неизменно весьма неустойчиво. Нелинейные возмущения координат изображения, такие как искажение объектива в моделях.

Дополнительные критерии могут также использоваться для классификации калибровки камеры:

• Неявные или явные модели. Фотограмметрическая подход с явным физически интерпретируемыми моделями калибровки, противопоставляется используемым неявным моделям, в структуре от алгоритмов движения, которые исправляют изображение, уточняют позиции в соответствии с требованиями к выравниванию реального проективного отображения (Hall et al., 1982; Wei & De Ma, 1994).

• Методы использования 3D, а не планарных точечных массивов (Triggs, 1998; Zhang, 2000). В то время как некоторые методы CV и фотограмметрическая самокалибровка может обрабатывать оба случая – с соответствующей геометрией сети – такие модели, как существенная матрица не может принимать плоские точечные массивы.

• Точечные и линейные методы (Fryer and Brown, 1986; Caprile & Torre, 1990). Точечные методы более популярны в фотограмметрии с единственным основополагающим подходом к сведению, а именно калибровкой с отвесом, что дает параметры искажения объектива, но не IO.

Более конкретная классификация может быть выполнена в соответствии с используемой методикой оценки и оптимизации параметров:

• Линейные методы довольно просты и быстры, но, как правило, не могут обрабатывать искажения объектива и нуждаться в массиве контрольных точек известных координат. Они могут включать решения с закрытой формой, но обычно упрощают модель камеры, что приводит к низким результатам точности. Известный DLT (Abdel–Aziz & Karara, 1971), который по существу эквивалентен основному матричному подходу, иллюстрирует такую ​​технику.

• Нелинейные методы, такие как расширенная модель уравнения коллинеарности, которая составляет основу самокалибрующей коррекции пучков, наиболее знакомы с гордограммистами. Строгое и точное моделирование параметров камеры IO и искажений объектива предоставляется (Brown, 1971) посредством итерационного процесса оценки наименьших квадратов.

• Комбинация линейных и нелинейных методов, в которых используется линейный метод для восстановления начальных приближений для параметров, после чего ориентация и калибровка итерационно уточняются (Faugeras & Toscani, 1986; Tsai, 1987; Weng et al., 1992). Heikkilä & Silven, 1997). Этот двухступенчатый подход в большинстве случаев был исключен для точной калибровки камеры с помощью описанной выше инструкции по регулировке пучка, что также неявно является двухэтапным процессом.

3. КАЛИБРОВКА КАМЕРЫ В КОМПЬЮТЕРНОМ ВИДЕНИИ

В калибровочных моделях машинного и компьютерного зрения традиционно использовались эталонные сетки, калибровочная матрица Kbeing определялась с использованием изображений известного массива точек объекта (например, шаблона шахматной доски). Обычно применяемые методы Tsai, (1987), Heikkila & Silven (1997) и Zhang (2000). Все они основаны на модели камеры обскуры и включают термины для моделирования радиальных искажений.

Модель калибровки Цая предполагает, что некоторые параметры камеры предоставляются изготовителем, чтобы уменьшить первоначальную догадку оценки. Он требует n признаков точек (n> 8) на изображение и решает проблему калибровки с набором из n линейных уравнений, основанных на ограничении радиального выравнивания. Используется модель радиального искажения второго порядка, в то время как не рассматриваются условия децентрализации искажения. Двухэтапный метод может справиться либо с одним изображением, либо с несколькими изображениями трехмерной или планарной калибровочной сетки, но координаты точки сетки должны быть известны.

Методика, разработанная Heikkila & Silven (1997), сначала извлекает исходные оценки параметров камеры с использованием решения с закрытой формой (DLT), а затем применяется нелинейная оценка наименьших квадратов с использованием алгоритма Левенберга-Марквардта для уточнения IO и вычисления параметры искажения. Модель использует два коэффициента как для радиального, так и для децентрализованного искажения, а метод работает с одним или несколькими изображениями и с 2D или 3D калибровочными сетками.

Метод калибровки Чжана требует, чтобы передняя панель была размещена в виде планарной сетки шахматной доски с разной ориентацией. Разработанный алгоритм использует извлеченные угловые точки шаблона шахматной доски для вычисления проективного преобразования между точками изображения n разных изображений с точностью до масштабного коэффициента. После этого внутренние и внешние параметры камеры восстанавливаются с использованием решения с закрытой формой, а термины радиального искажения третьего и пятого порядка восстанавливаются в линейном решении наименьших квадратов. Окончательная нелинейная минимизация ошибки повторения, решаемая с использованием метода Левенберга–Марквардта, уточняет все восстановленные параметры. Подход Чжана очень похож на подход Триггса (1998), который требует не менее 5 просмотров планарной сцены.

Термин самокалибровка (или автокалибровка) в CV используется, когда не используется объект калибровки, а метрические свойства камеры и изображенной сцены восстанавливаются из набора «некалиброванных» изображений с использованием ограничений на параметры камеры или на изображенной сцене. Самокалибровка обычно применяется в 3D-моделировании для обновления проективной реконструкции до единицы, которая является метрической (то есть произвольное евклидово преобразование и масштабный множитель). В общем случае применяются три типа ограничений (отдельно или совместно) для выполнения самокалибровки: ограничения сцены, ограничения движения камеры или ограничения на встроенные параметры камеры. Все они были опробованы, но в случае неизвестного движения камеры и неизвестной сцены могут использоваться только ограничения на IO.

Большинство так называемых алгоритмов самокалибровки, описанных в CV - литературе, относятся к параметрам внутренней камеры как постоянным, но неизвестным (Faugeras et al., 1992; Hartley, 1994; Pollefeys & Van Gool, 1996; Heyden & Åström, 1996; Triggs ,1997). Проблема переменных параметров IO также изучалась Pollefeys et al. (1997) и Heyden & Åström (1997). Самокалибровка может быть проблематичной с некоторыми сетями критической последовательности движения (Sturm, 1997), где движение камеры обычно недостаточно для восстановления параметров калибровки, и неоднозначность остается в 3D-реконструкции. Более того, только фокусное расстояние обычно определяется, когда искажение объектива и другие внутренние параметры игнорируются, считаются известными или считаются неизвестными и восстанавливаются без какого-либо статистического тестирования для значимости.

Из вышеприведенного обсуждения одна из особенностей приближения CV к калибровке камеры очевидна: до сих пор нет принятого метода в один шаг, который является либо достаточно универсальным, либо пригодным для полной автоматизации. Это не удивительно, учитывая характеристики аппаратного обеспечения изображения (например, объективы с переменным масштабированием) и геометрии изображений, принятые во всем спектре приложений CV.

4. КАЛИБРОВКА ФОТОГРАММНОЙ КАМЕРЫ

4.1 Обзор

Различные модели фотоаппаратов были сформулированы и использованы в фотограмметрии, но, как правило, ориентация и калибровка датчика выполняются с помощью перспективной геометрической модели с помощью регулировки пучка (Brown, 1971). Обзор методов и моделей последних 50 лет представлен в Clarke & Fryer (1998). Основная математическая модель обеспечивается уравнениями нелинейной коллинеарности, обычно расширенными поправочными членами (то есть дополнительными параметрами или точками доступа) для IO радиального и децентрализованного искажения линз (Fraser, 1997; Gruen & Beyer, 2001). Коррекция пучка обеспечивает одновременное определение всех параметров системы наряду с оценками точности и надежности извлеченных параметров калибровки. Кроме того, можно количественно определить корреляции между параметрами IO, внешней ориентации (EO) и координатами объектных точек, а также их определяемостью.

Требуется благоприятная сетевая геометрия, то есть должны быть получены конвергентные и повернутые изображения предпочтительно трехмерного объекта с хорошо распределенными точками по всему формату изображения. Если сеть является геометрически слабой, корреляции могут приводить к неустойчивости оценки наименьших квадратов. Использование несоответствующих точек доступа также может ослабить решение по настройке пучка, что приводит к чрезмерной параметризации, в частности, в случае минимально ограниченных настроек (Fraser, 1982).

Настройка самокалибровки пучков может выполняться с ограничениями пространства объектов или без них, которые обычно находятся в форме известных контрольных точек. Минимальное ограничение для определения сетевой привязки всегда требуется, хотя это может быть связано с неявными средствами, такими как внутреннее ограничение, регулировка свободной сети или с помощью явной минимальной конфигурации контрольной точки (произвольной или реальной). Калибровка с использованием тестового поля возможна, хотя одним из достоинств самокалибровки является то, что она не требует предоставления какой-либо информации контрольной точки. Восстановление калибровочных параметров с одного изображения (и трехмерного тестового поля) также возможно с помощью модели коллинеарности, хотя эта пространственная резекция с точками доступа не получила широкого применения из–за требования к точному тестовому полю и предоставленной ниже калибровке точности.

Одним из традиционных препятствий для более широкого применения корректировки самокалибровки пучков вне сообщества фотограмметрии было понимание того, что вычисление начальных приближений параметров для итеративного решения наименьших квадратов ка–то «затруднено». Это уже во многих отношениях не так. Как будет упомянуто позже, самокалибровка через регулировку пучка может быть полностью автоматическим процессом, требующим не более того изображений, записанных в подходящей геометрии множества станций, первоначальной догадки фокусного расстояния (и это может быть предположение), и имитируемые кодированные объекты, которые образуют массив точек объекта.

5. ПРОЕКТНЫЕ СООБРАЖЕНИЯ

Критически важным для качества самокалибровки является общая геометрия сети и, в частности, конфигурация камеры. Различные экспериментальные исследования в области ближней фотограмметрии (например, Fraser, 1996; Fryer, 1996; Clarke et al., 1998; Gruen & Beyer, 2001; El-Hakim et al., 2003) подтвердили, что:

• Точность сети увеличивается с увеличением углов сходимости изображений. Увеличение углов сходимости также неявно означает увеличение базового отношения (B / D).

• Точность повышается за счет увеличения количества лучей до заданной точки объекта, хотя скорость улучшения пропорциональна квадратному корню из числа изображений, «видящих» точку. Таким образом, выигрыш в точности эффективно выравнивается после, скажем, 8 лучей на точку.

• Точность увеличивается с количеством измеренных точек на изображение, но постепенное улучшение незначительно за несколько десятков точек. Более важно то, что дополнительные точки в изображении предлагают лучшие перспективы для моделирования отклонения от коллинеарности во всем полном формате изображения.

• Самокалибровка является надежной только в том случае, когда геометрия сети благоприятна, то есть конфигурация камеры содержит высоко сходящиеся изображения, ортогональные углы рулона и большое количество хорошо распределенных точек объекта. Компенсация отклонения от коллинеарности вполне может быть достигнута при корректировке связки с точками доступа для слабой сети, но точное и надежное восстановление типичных калибровочных значений будет получено с меньшей вероятностью.

• Для калибровки камеры можно использовать массив плоских объектных точек, если изображения получены с ортогональными углами рулона, с высокой степенью сходимости и желательно с различными расстояниями между объектами. Требуется максимально возможное изменение масштаба изображения в формате изображения.

• Как упоминалось, должны присутствовать углы ортогонального валка, чтобы разрушить проективную связь между параметрами IO и EO. Несмотря на то, что можно было бы достичь этой развязки без поворотов изображения 90^o, благодаря обеспечению массива трехмерных объектов, всегда рекомендуется иметь «свернутые» изображения в сети самокалибровки.

6. ЭКСПЕРИМЕНТАЛЬНЫЕ ИСПЫТАНИЯ

В этом разделе представлены отдельные результаты экспериментальных испытаний на самокалибровку, в которых кратко рассматриваются три вопроса. Первое – это различие в достижимой точности между CV и фотограмметрическими подходами. Второе подчеркивает часто упущенные проблемы, связанные с несоответствующей геометрией сети для калибровки, а третья – для иллюстрации того, что остаются проблемы исследовательской заинтересованности в моделировании параметров камеры.

6.1 Калибровка камеры с использованием 3D-объекта

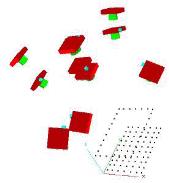
Сравнение между различными методами проводилось с использованием 3D-теста и 10 изображений, полученных с помощью цифровой камеры Leica Digilux 1 при разрешении изображения 1120 x 840 пикселей. 3D-массив точек объекта и геометрия камеры показаны на рисунке 2. Фокусное расстояние фиксировалось при минимальном увеличении (самый широкий угол), а сеть включала четыре изображения с ± 90 ° углов. Были применены следующие программные комплекты или алгоритмы калибровки камеры: DLT (Abdel–Aziz & Karara, 1971), реализованный в IGPETH Zurich без коррекции искажений.

 • Tsai (Tsai, 1987), с первым членом коррекции радиального искажения; доступ через www-cgi.cs.cmu.edu/afs/cs.cmu.edu /user/rgw/www/TsaiCode.html.

• Heikkila (Heikkila & Silven, 1997), с двумя терминами для коррекции радиальных и децентрализованных искажений; доступный по адресу www.ee.oulu.fi/~jth/calibr/.

• Фотомодель (www.photomodeler.com) с полным набором точек доступа без контрольных точек.

• Australis (www.photometrix.com.au) с полным набором точек доступа в режиме свободной сети.

• SGAP, реализованный в Цюрихе IGP-ETH, с полным набором точек доступа в режиме свободной сети.

В рамках процесса самокалибровки Photomodeler, Australis & SGAP значения параметров могут быть ограничены с помощью первоначально назначенных стандартных ошибок, тогда как для других методов доступно несколько вариантов. Результаты калибровок, оцененные полученным RMSE координатами координат изображения (разметки триангуляции) и RMSE координат точки объекта XYZ с их истинными значениями, приведены в таблице 1. Восстановленные профили радиального искажения из каждого решения также показаны в Рисунок 1, но следует напомнить, что с фотограмметрической точки зрения основным индикатором качества калибровки являются значения RMSE координат точек объекта (таблица 1), и здесь можно видеть, что корректировки пучка дают превосходные результаты.

Таблица 1. Точность точки объекта и остатки от различных калибровочных вычислений.

6.2 Калибровка камеры с использованием планарной целевой массива

Был также выполнен еще один калибровочный тест камеры, на этот раз с массивом планарных объектов, а именно черно-белым рисунком шахматной доски. Данные изображения были получены с http://www.vision.caltech.edu/bouguetj/calib_doc/, где доступен набор инструментов для калибровки камеры, разработанный Я. В. Буге из Caltech. Используемые 25 изображений имели разрешения 640 x 480 пикселей. В этом случае камера была зафиксирована, а поле планарных точек, показанное на рисунке 3, перемещалось по различным направлениям – хотя, в частности, без поворотов на 90^o.

Самокалибровки для этого теста снова проводились с использованием Photomodeler, Australis, SGAP и методов Tsai и Heikkila, а также применялся метод Zhang. Хотя восстановленные параметры камеры были весьма схожими, статистические показатели качества, доступные в Australis и SGAP, показали, что сеть по сути является сингулярной из-за отсутствия изменения угла наклона валка. Это приводит к очень высокой проективной связи между параметрами IO и EO. Фактически, можно существенно заменить любое правдоподобное значение для главного смещения точки (xp, yp), и будет получено удовлетворительное и близкое к постоянному RMSE остатков (между 0,57 и 0,63 микрон), как показано на рисунке 3. То же самое true для детерминирующих параметров P1 и P2 децентрализации, а их включение или упущение не имеет никакого отношения к восстановленным значениям RMSE остатков изображения. Это означает, что сеть (без повернутых изображений) может вмещать любое смещение основной точки (в пределах разумного) и, следовательно, она не имеет силы для восстановления «истинных значений». Это делает процесс калибровки практически бесполезным, если отыскиваются независимые параметры камеры.

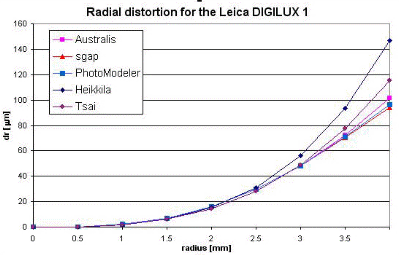
Рисунок 1. Калибровка тестового поля и геометрии сети изображений (выше),наряду с вычисленными профилями радиального искажения.

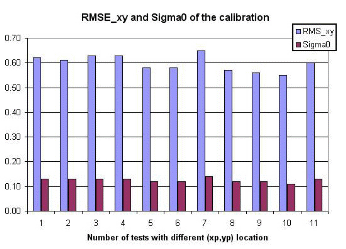
Рисунок 2. Изображение планарного тестового поля и геометрии камеры (см. Выше), а также восстановленные остатки и апостериорные значения сигма из 11 Australis трасс (см. Ниже).

6.3 Радиальное искажение в разных цветовых каналах

В настоящее время очень сложно найти монохромную офсетную цифровую камеру. Для высокоточного фотограмметрического измерения возникают новые проблемы калибровки с цветными камерами. Одна из таких проблем – эффект хроматической аберрации внутри линзы, которая обычно делится на продольные (осевые) и боковые (наклонные) аберрации. Первый создает эффекты размытия, которые трудно уменьшить, в то время как последний вызывает степень неправильной регистрации цветовых каналов, которые могут быть исправлены на этапах последующей обработки (Cronk et al., 2006). Фактор, который может неблагоприятно влиять на точность этой регистрации и на восстановление репрезентативных профилей искажений объективов в пределах настройки самокалибровки, – это различие между профилями искажений отдельных цветовых каналов.

Этот аспект был исследован для цифровой камеры SONY DSC F828 (8 мегапикселей) с фокусным расстоянием 10 мм. Полученные профили, показанные на рисунке 4, показывают, что радиальное искажение в зеленом канале является наименьшим, тогда как в синем канале наибольшее (разница достигает около 10 пикселей на краях сенсора). В фотограмметрических измерительных приложениях, требующих высокой точности, необходимо учитывать такие влияния дифференциальных искажений, особенно учитывая, что большинство цветных ПЗС-камер используют фильтры Байера. Двумя возможными параметрами являются, во-первых, запись одноцветных изображений с использованием внешнего фильтра (например, зеленый фильтр, поскольку шаблон Bayer имеет в два раза больше зеленых пикселей, чем красный или синий), а во–вторых, для самокалибровки искажений объектива для каждый цвет и затем корректировать искажения отдельно в каждом канале до того, как будут измерены окончательные «зарегистрированные» изображения RGB. Практическая трудность с этим подходом заключается в том, что он обычно требует доступа к «необработанным» изображениям камеры, функции, которые могут быть доступны или недоступны в недорогих камерах.

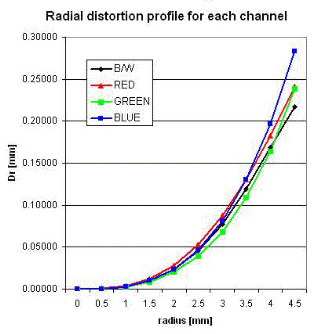
Рисунок 3. Радиальные профили искажений для 3-х цветных каналов и черно-белое изображение.

7. ВЫВОДЫ

В этой статье рассмотрены различные подходы к калибровке цифровой камеры. Поскольку использование камер потребительского класса становится все более распространенным в фотограмметрических приложениях, существует потребность в принятии соответствующих процедур калибровки. Настройка самокалибровки пучков является очень гибким и мощным инструментом для калибровки камеры и систематической компенсации ошибок, а также обеспечивает точную обработку датчиков и объектов при одновременном рассмотрении всех неизвестных систем как стохастических переменных.

Не всегда возможно выполнить самокалибровку в практических проектах измерения с близкого расстояния. Фактически, геометрия сети, оптимальная для реконструкции сцены, часто отличается от тех, которые поддерживают всестороннюю калибровку камеры. Поэтому, вместо того, чтобы выполнять самокалибровку одновременно с реконструкцией объекта, часто лучше сначала откалибровать камеру с использованием соответствующей сети с целью восстановления всех значимых параметров (а не только фокусного расстояния, как во многих приложениях CV). В настоящее время калибровка может быть полностью автоматической процедурой, и опыт показывает, что временные изменения параметров калибровки для камер потребительского класса, как правило, незначительны, учитывая, что они используются на низких и средних уровнях точности.

ЛИТЕРАТУРА

1. Abdel-Aziz, Y.I. and Karara, H.M., 1971: Direct linear transformation into object space coordinates in close-range photogrammetry. Proc. Symposium on Close-Range Photogrammetry, pp. 1-18

2. Abraham, S. and Hau, T., 1997: Towards autonomous highprecision calibration of digital cameras. Proceedings of SPIE Videometrics V, El-Hakim (Ed.), Vol. 3174, pp. 82-93

3. Bösemann, W., Godding, R., and Riechmann, W., 1990: Photogrammetric investigation of CCD cameras. In ‘Close Range Photogrammetry Meets Machine Vision’, Gruen and Baltsavias (Eds), SPIE Vol. 1395, pp. 119-126

4. Brown, D.C., 1971: Close-range camera calibration. PE&RS, Vol. 37(8), pp.855-866 Clarke, T.A. and Fryer, J.G., 1998: The development of camera calibration methods and models. The Photogrammetric Record, Vol. 16(91), pp. 51-66

5. Clarke, T.A., Fryer, J.G. and Wang, X., 1998: The principal point and CCD cameras. The Photogrammetric Record, Vol. 16(92), pp. 293-312

6. Cronk, S., Fraser, C.S. and Hanley, H.B. (2006) Automatic Calibration of Colour Digital Cameras. Photogammetric Record (in press).

7. D'Apuzzo, N. and Maas, H.-G., 1999: On the suitability of digital camcorders for virtual reality image data capture. Proceedings of SPIE Videometrics VI, El-Hakim and Grue (Eds.), Vol. 3461, pp. 259-267

8. El-Hakim, S., Beraldin, J. and Blais, F., 2003: Critical factors and configurations for practical 3D image-based modeling. 6th Conference on Optical 3D Measurements Techniques, Zurich, Vol.2, pp.159-167

9. Faugeras, O. and Toscani, G., 1986: The calibration problem for stereo. IEEE CVPR, pp. 15-20

10. Faugeras, O., Luong, Q.T. and Maybank, S., 1992: Camera selfcalibration: Theory and experiments. ECCV'92, Lecture Notes in Computer Science, Vol. 588, Springer-Verlag, pp. 321-334

11. Fraser, C.S., 1980: Multiple focal setting self-calibration of close-range metric cameras. PE&RS, 46(9), pp. 1161-1171 Fraser, C.S., 1982: On the use of non-metric cameras in analytical non-metric photogrammetry. Int. Archives of Photogrammetry and Remote Sensing, Vol. 24(5), pp. 156-166

12. Fraser, C. S. and Shortis, M., 1995: Metric exploitation of still video imagery. The Photogrammetric Record, 15(85): 107-122

13. Fraser, C.S., 1996: Network design. In ‘Close-range Photogrammetry and Machine Vision’, Atkinson (Ed.), Whittles Publishing, UK, pp.256-282

14. Fraser, C.S., 1997: Digital camera self-calibration. ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 52, pp. 149-159

15. Fraser, C.S., 2001: Photogrammetric camera component calibration. A review of analytical techniques. In ‘Calibration and Orientation of Cameras in Computer Vision’, Gruen and Huang (Eds.), Springer Series in Information Sciences 34, pp. 95-121

16. Fraser, C.S. and Al-Ajlouni, S., 2006: Zoom-dependent camera calibration in digital close-range photogrammetry. PE&RS, (in press)

17. Fryer, J. and Brown, D., 1986: Lens distortion for close-range photogrammetry. PE&RS, Vol. 52(1), pp.51-58

18. Fryer, J., 1996: Camera Calibration. In ‘Close-range Photogrammetry and Machine Vision’, Atkinson (Ed.), Whittles Publishing, UK, pp.156-179

19. Ganci, G. & Handley, H., 1998: Automation in videogrammetry. Int. Archives of Photogrammetry and Remote Sensing, 32(5): 53-58.

20. Gruen, A., 1981: Precision and reliability aspects in close-range photogrammetry. Photogrammetric Journal of Finland, Vol. 8(2), pp. 117-132

21. Gruen A. and Beyer, H.A., 2001: System calibration through self-calibration. In ‘Calibration and Orientation of Cameras in Computer Vision’ Gruen and Huang (Eds.), Springer Series in Information Sciences 34, pp. 163-194

22. Hall, E.L., Tio, J.B.K., McPherson, C.A. and Sadjadi, F.A., 1982: Measuring curved surfaces for robot vision. Computing Journal, Vol. 15, pp. 42-54

23. Hartley, R., 1994: Euclidean reconstruction from uncalibrated views. In ‘Applications of Invariance in Computer Vision’, Mundy, Zisserman and Forsyth (eds.), Lecture Notes in Computer Science, Vol. 825, Springer-Verlag, pp. 237-256

24. Heikkilä, J. and Silven, O., 1997: A four-step camera calibration procedure with implicit image correction. CVPR97

25. Heyden, A. and Aström, K., 1996: Euclidean Reconstruction from Constant Intrinsic Parameters. IEEE CVPR, pp. 339-343

26. Heyden, A. and K. Aström, 1997: Euclidean Reconstruction from Image Sequences with Varying and Unknown Focal Length and Principal Point. Proc. IEEE CVPR, pp. 438-443

27. Jantos, R., Luhmann, T., Peipe, J., Schneider, C.-T., 2002: Photogrammetric Performance Evaluation of the Kodak DCS Pro Back. Int. Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. 33(5), Corfu, Greece

28. Kunii, Y. and Chikatsu, H., 2001: On the application of 3 million consumer digital camera to digital photogrammetry. Proceedings of SPIE Videometrics VII, Vol. 4309, pp. 278-287

29. Läbe, T. And Förstner, W., 2004: Geometric stability of lowcost digital consumer cameras. Int. Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. 35(5), pp 528-535, Istanbul, Turkey

30. Peipe, J. and Stephani, M., 2003: Performance evaluation of a 5 megapixel digital metric camera for use in architectural photogrammetry. Int. Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. 34 (5/W12), pp. 259-261 Pollefeys, M., Van Gool, L. and Oosterlinck, A., 1996: The Modulus Constraint: A New Constraint for Self-Calibration. Proc. 13th IEEE CVPR, pp. 349-353

31. Pollefeys, M., Koch, R. and Van Gool, L., 1997: Self- Calibration and Metric Reconstruction in spite of Varying and Unknown Internal Camera Parameters. IEEE ICCV, pp. 90-95

32. Remondino, F. and Borlin, N., 2003: Photogrammetric calibration of image sequences acquired with a rotating camera. Int. Archives of Photogrammetry and Remote Sensing, Vol. 34(5/W16)

33. Salvi, J., Armanguè, X. and Batlle, J., 2002: A comparative review of camera calibration methods with accuracy evaluation. Pattern Recognition, Vol. 35, pp. 1617-1635

34. Shortis, M., and Beyer, H.A., 1997: Calibration stability of the Kodak DCS420 and 460 cameras. Proceedings of SPIE Videometrics V, Vol. 3174

35. Sturm, P., 1997: Critical Motion Sequences for Monocular Self- Calibration and Uncalibrated Euclidean Reconstruction'. Proc. IEEE CVPR, pp. 1100-1105

36. Tsai, R.Y., 1987: A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE Int. Journal Robotics and Automation, Vol. 3(4), pp. 323-344

37. Triggs, B., 1997: The Absolute Quadric. Proc. IEEE CVPR, pp. 609-614 Trigg, B., 1998: Autocalibration from planar scenes. ECCV 98, pp. 89-105

38. Wei, G. and De Ma, S., 1994: Implicit and explicit camera calibration: theory and experiments. IEEE Trans. on PAMI, Vol. 16(5), pp. 469-479

39. Weng, J., Cohen, P. and Herniou, M., 1992: Camera calibration with distortion models and accuracy evaluation. IEEE Trans. On PAMI, Vol. 14(10), pp. 965-980

40. Wiley, A.G. and Wong., K.W., 1995: Geometric calibration of zoom lenses for computer vision metrology. PE&RS, Vol. 61(1), pp. 69-74

41. Zhang, Z., 2000: A flexible new technique for camera calibration. IEEE Trans. on PAMI, Vol. 22(11), pp. 1330-1334