Относительно недорогие и потому доступные цифровые камеры, не предусматривающие фотолабораторный процесс, позволяют получать цветное изображение, непосредственно загружаемое в компьютер. Это вызвало многочисленные попытки использовать подобные снимки как исходный материал для измерений различных объектов дистанционным методом. Конечно, такие камеры по точности результатов не в состоянии конкурировать со специальной аппаратурой, но имеется большой круг задач, где они могут успешно применяться.

При фотограмметрической обработке снимков требуется знание элементов внутреннего ориентирования (ЭВО) камеры и данных о дисторсии, которая в камерах, не предназначенных для измерительных целей, может достигать заметных величин. Поскольку паспортные данные таких сведении не содержат возникает необходимость в калибровке камер. Способ лабораторной калибровки, пригодный для практического применения, должен отвечать следующим требованиям: относительная простота создания тест–объекта и его компактность; возможность полной калибровки, т. е. определения ЭВО и дисторсии; минимальный объем измерений по снимкам. Вместе с тем в ряде случаев достаточно частичной калибровки, т. е. определения только дисторсии, например, для исследования ортоскопичности объектива камеры или получения поля дисторсии для коррекции изображений плоских объектов.

Лабораторный способ, в определенной мере отвечающий этим требованиям, основан на съемке с близкого расстояния тест–объекта и измерения на снимке в ручном режиме пиксельных координат точек. Дальнейшая обработка результатов измерений основывается на уравнениях коллинеарности

  (1)

где х, у – координаты точки в системе снимка;  x ₀ ,  y ₀ ,  f   – элементы внутреннего ориентирования: координаты главной точки и фокусное расстояние;  a _k ,  b _k ,  c _k  – направляющие косинусы – функции угловых элементов внешнего ориентирования снимка ; ;  X _G ,Y _G , Z _G  – геодезические координаты точки в системе тест–объекта;  X _S ,Y _S , Z _S  – координаты центра проекции снимка в системе тест–объекта.

Уравнения (1) после приведения к линейному виду можно представить формулой

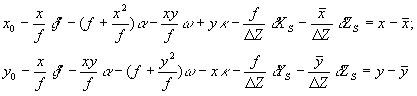  (2)

где  – поправка в приближенно принятое фокусное расстояние;  – поправки в приближенно принятые координаты центра проекции;  – координаты точки, вычисленные по (1) на основе приближенно принятых неизвестных. Начальные значения  x ₀ ,  y ₀  и  практически могут приниматься равными нулю.

Из решения системы уравнений (2), составленных для точек с известными геодезическими координатами, определяются элементы внешнего и внутреннего ориентирования снимка. Система решается итеративно по методу наименьших квадратов. При каждой итерации с приближенно заданными исходными данными по (1) создается макетный снимок под условием минимальных расхождений вычисленных и измеренных значений плоских координат точек, т. е. снимок, максимально приближенный к реальному. После последней итерации определяются значения ЭВО и вычисляется дисторсия

  (3)

Следовательно, для калибровки достаточно измерений по одному снимку. Для полной калибровки необходим рельефный тест–объект. Если ставится задача частичной калибровки, т. е. определения только дисторсии, то из уравнений (2) исключаются по два первых члена, содержащих ЭВО, и число неизвестных сокращается до шести. В этом случае тест–объект может быть плоскостью. По плоскому тест–объекту возможна и полная калибровка, но при условии, что в той же системе известны и координаты центра проекции снимка. Однако определение их с необходимой точностью при малых расстояниях съемки – задача технически весьма непростая.

Таким образом, задача калибровки решается на основе сравнения реального снимка с макетным, т. е. идеальным. При малых значениях дисторсии, сопоставимых со случайными ошибками измерений, задача калибровки на данном этапе будет выполнена. Примером такой камеры может служить, например, Kodak DC210+. Иначе обстоит дело при калибровке камер со значительной дисторсией, присущей некоторым из них. Она вносит заметные деформации в результаты обратной засечки, а следовательно, и в результаты калибровки. Примером в данном случае является камера Nicon COOLPIX 950.

Если съемка проведена камерой с большой дисторсией, то калибровка и обработка снимков имеют свои особенности. Прежде всего для устранения искажения снимка изображение на основании данных калибровки должно быть преобразовано. Тогда теоретически по своей геометрии оно будет полностью соответствовать макетному, т. е. нелинейные искажения отсутствуют, связка лучей отвечает требованию ортоскопичности объектива: , где  – направления на точки в поле предмета и в поле изображения [4]. Однако векторы дисторсии, полученные на основе рельефного тест–объекта, частично зависят от расположения рельефных точек. Поэтому полную калибровку камеры целесообразно проводить в два этапа, используя два снимка.

Тест–объект фотографируется дважды: в плоском и рельефном вариантах. Поле дисторсии определяется по первому снимку на основе неполных уравнений (2). Как показывает практика, оно хорошо описывается полиномами 3–го порядка. По этим данным проводится коррекция второго, рельефного, изображения, т. е. получается практически свободный от нелинейной дисторсии снимок, который и измеряется. По данным измерений на основе полных уравнений (2) вычисляются значения ЭВО. За дисторсию корректируются все снимки, предназначенные для фотограмметрической обработки. Для контроля получают стереопару снимков на рельефный тест–объект, и по ним после корректирования за дисторсию проводится построение фотограмметрической модели и ее внешнее ориентирование по координатам точек тест–объекта. Сравнение фотограмметрических координат с геодезическими дает представление о точности модели и косвенно о качестве калибровки.

Таким образом, при незначительной дисторсии предлагаемый способ обеспечивает полную калибровку по одному снимку рельефного тест–объекта. Для полной калибровки изображений с большой дисторсией требуются два снимка: плоский и рельефный тест–объект, а для контроля – дополнительно вспомогательная стереопара, хотя она в процессе калибровки не участвует.

Современные технологии обработки цифровых изображений дают возможность их преобразования по данным калибровки, что сводит к минимуму влияние дисторсии (например, системы ENVI и ERDAS imagine). После такого корректирования снимки могут быть использованы для построения фотограмметрических моделей. В нашем случае данные калибровки для этих систем представляются в виде таблицы, в которой для каждой точки тест–объекта даются координаты, измеренные, на исходном снимке и вычисленные для макетного снимка. На основе таблицы с помощью корректирующей системы создается модель для учета искажении любого снимка, параметры которого соответствуют снимку с изображением тест–объекта. Какие–либо дополнительные измерения при этом не требуются. Учет дисторсии предусмотрен и в некоторых фотограмметрических системах, например в системе Фотомод, где учитывается строго радиальная и симметричная дисторсия. Представляется, однако, что предварительное преобразование снимков может быть эффективнее, поскольку нет ограничений по радиальности и симметрии, а ЭВО определены по снимку, преобразованному аналогично всем прочим. Но этот вопрос требует специальных исследований.

Изготовление с достаточной точностью рельефного тест–объекта – работа, требующая аккуратности. Один из возможных вариантов представлен в предлагаемой конструкции (рис. 1). Основой ее является выверенная горизонтальная плоскость размером примерно 90 х 70 см. На плоскости крепится лист ватмана или пластика с нанесенными через 10 см посредством координатографа крестообразными метками. Для имитации рельефа служит конструкция, изготовленная из уголкового алюминия (50 х 50 х 2 мм), размером 80 х 60 х 35 см.

Рис. 1. Общий вид лабораторного тест–объекта

По верху через 10 см нанесены маркированные точки. Конструкция кладется на плоскость, ее углы совмещаются с точками графической разметки. Таким путем создастся единая система координат для верхних и нижних маркированных точек. Тест–объект данной конструкции удобнее использовать и для предварительного упрощенного определения фокусного расстояния. Для этого служит формула

  (4)

где  l ₁ , l ₂  – измеренные по снимку два горизонтальных отрезка длиной  L , один из которых лежит на координатной плоскости тест–объекта, другой – на рельефной его части на высоте  h . Для уменьшения влияния наклона снимка отрезки следует располагать по диагоналям тест–объекта симметрично центру снимка. Результат вычислений по формуле (4) будет близок к результату, который дает решение системы (2).

При фотографировании тест–объекта с близкого расстояния приходится иметь дело со случаями, когда фокусировка камеры, устанавливаемая с учетом ее будущего рабочего положения, не соответствует реальному расстоянию съемки при калибровке. Эти несоответствия различны в зависимости от того, калибруется камера для использования в ближней фотограмметрии или для съемки отдаленных объектов и соответственно фокусируется. Возникает некоторая размытость изображений маркированных точек. Определить степень размытости можно на основании приводимого ниже расчета.

Если принять следующие обозначения:  Z _F  – расстояние съемки, на которое отфокусирована камера;  Z _К  – расстояние при калибровке до тест–объекта;  l _F , l _K  – соответствующие им расстояния в поле изображения;  F  – фокусное расстояние объектива камеры;  d  – действующее отверстие диафрагмы;  – диаметр кружка нерезкости, то очевидно

  (5)

Из основного уравнения линзы следует

  (6)

После преобразования имеем

  (7)

Для перехода к пиксельным единицам следует умножить (7) на соотношение  f / F.  где  f  – фокусное расстояние объектива в пикселях,  F –  в миллиметрах. Выражая расстояния до снимаемого объекта в метрах и пренебрегая в знаменателе значением  F, получаем рабочую формулу

  (8)

где   –  величина кружка нерезкости, выраженная в пикселях.

Для многих цифровых камер, например Kodak DC210, Olimpus C21, Nikon COOLPIX, отношение длины фокусного расстояния к длине цифровой матрицы составляет 1,2–1,5. Поэтому при размерах тест–объекта 80 х 60 см с учетом его рельефа для заполнения изображением всего снимка необходимо вести съемку с расстояния 1,3–1,5 м. Приведем в качестве примера расчет величины кружка нерезкости для камеры Nikon при фокусировке ее на различные расстояния. Параметры камеры:  F  = 7,2 мм,  f  = 1800 пкс. Принимая Z _К   =  1 м,  D  = 7, получаем по (8) результаты, представленные в таблице.

Из таблицы следует, что при фокусировке практически на любое расстояние, вплоть до гиперфокального, и съемке с расстояния 1 м с диафрагмой 7 кружок нерезкости не превысит 1,8 пкс. Из расчетов следует также необходимость хорошего освещения при съемке для калибровки в целях достаточного диафрагмирования камеры.

При оценке влияния размытости изображения на точность измерений следует учитывать дискретность как отсчетов, так и самого изображения. Точечный объект, сопоставимый по размеру с пикселем, в зависимости от положения точки на матрице может дать изображение более пикселя. На рнс. 2 показаны различные варианты размытости точки изображения. Для неразмытой точки (внутренняя окружность и клеточная штриховка) изображения получаются в пределах 1–4 пикселей. Размытая точка с кружком 1,8 дает дополнительные изображения, показанные на рис. 2 наружной окружностью и продольной штриховкой. Изображения размытой точки могут занимать 4–б пикселей. При измерении оператор наводит марку на центр изображения и берет отсчеты с определенным шагом. Оптимальным в данном случае является шаг в 0,5 пикселя. Согласно закону распределения равной вероятности [3], средняя квадратическая ошибка отсчета из–за округления равна , где – предельная абсолютная ошибка, равная в нашем случае 0,25 пкс. Следовательно, средняя квадратическая ошибка из–за округления будет равна  пкс. Практика измерений показывает, что при повторных наведениях отсчеты разнятся не более чем на 0,5 пкс. Эту величину можно считать удвоенной средней квадратической ошибкой наведения 0.25 пкс. Сложение ее с ошибкой округления отсчетов дает 0,3 пкс, что можно принять как случайную среднюю квадратическую ошибку измерений, в том числе и для размытого изображения, исходя из того, что центры размытого к неразмытого изображений совпадают. Это допущение подтверждается практикой измерении. Таким образом, можно считать, что не–резкость изображения не вносит о существенных ошибок при измерениях тест–объекта, и среднюю квадратическую ошибку можно принять равной 0,3 пкс при предельном значении 0,5 пкс.

На точность калибровки и определения ЭВО, в частности, влияет число точек, в том числе верхних. Расчеты показывают, что при высоте конструкции 35 см, общем числе точек 91, из которых 28 верхние, весовые коэффициенты для  f, x ₀ ,  y ₀  будут равны соответственно 7,0; 3,1; 5,5. Принимая ошибку единицы веса 0,3 пкс, получаем теоретические значения ошибок определения ЭВО – , где  – соответствующий весовой коэффициент. Расчет дает значения ошибок ЭВО: 0,8; 0,5; 0,7 пкс. Таким образом, влияние случайных ошибок измерения на определяемые ЭВО можно принять близким к 0,5–1 пкс, хотя может иметь моего и влияние ошибок построения тест–объекта, главным образом точность изготовления его рельефной части. Исходя из разрешения изображений, т. е. соотношения  Z / f , и принимая  Z   =  1000 мм,  f  = 1800 пкс, получаем 0,5 мм/пкс. Отсюда следует, что точность изготовления тест–объекта должна быть порядка 0,5 мм. Основным источником возможных ошибок может быть неперпендикулярность вертикальных стоек к основной плоскости, что приводит прежде всего к ошибкам определения координат главной точки. В значительной мере компенсировать их можно, если фотографировать тест дважды, поворачивая верхнюю конструкцию на 180°. Средний результат калибровки по двум снимкам будет в значительной степени свободен от этих ошибок.

При измерениях реальных снимков тест–объекта нами использовалась система Фотомод. Хотя она не предназначена для измерений одиночного снимка, но возможности се базового модуля при введении опорных точек позволяют это сделать. Для подобных целей можно использовать и компьютерный стереокомпаратор фирмы ИБИК [5].

Рис. 2. Варианты размытости точки изображения вследствие неадекватной фокусировки объектива: а – центр пикселя, б – граница двух пикселей, в – стык четырех пикселей (прямыми линиями отмечены границы пикселей)

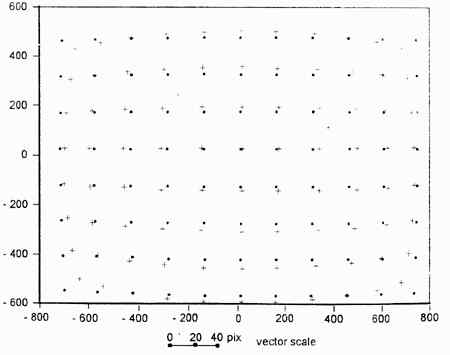
Рис. 3. Векторная диаграмма дисторсии для камеры Nikon COOLPIX 950, полученная путем съемки плоского тест–объекта

Проверка способа проведена на макетных и реальных снимках. Для экспериментов с реальными снимками были использованы цифровые камеры Nikon COOLPIX 950 и Kodak DC210+. Ими проводилась съемка тест–объекта с отклонением оптической оси от перпендикуляра к его плоскости, как правило, не более 1 ^о . На рис. 3 приведена векторная диаграмма дисторсии для камеры Nikon, полученная изложенным способом, из которой следует, что максимальные значения дисторсии достигают 15–17 пкс. Результаты калибровки камеры Kodak показали, что максимальное значение дисторсии на краях кадра не превышает 1,5 пкс при среднем квздратическом 0,5 пкс, причем значения ЭВО оказались весьма близкими (в пределах 2–3 пкс) к тем, которые были получены для нее способом эталонного снимка [1]. Это естественно, так как в данном случае обратная засечка практически не была искажена дисторсией. В то же время результаты для камеры Nikon несколько отличались от полученных этим способом: на обратной засечке сказалось влияние дисторсии. Этот пример иллюстрирует тот факт, что способ калибровки при большой дисторсии влияет на значение ЭВО, как и на определяемые элементы дисторсии. Однако учет последней, совместно с получаемым фокусными расстоянием, дает возможность построения фотограмметрической модели, подобной объекту.

В процессе эксперимента камерой Nikon проводились контрольные стереосъемки тест–объекта с последующим корректированием снимков и построением фотограмметрических моделей. Максимальные остаточные значения дисторсии после коррекции снимков не превышали 1,5–2 пкс в углах кадра при средних квадратических значениях но полю 0,5–0,6 пкс. Стереосъемка тест–объекта в целях полного его захвата проводилась с углом конвергенции 15. На рис. 4 показан один из таких снимков: исходный и после коррекции изображения.

После построения фотограмметрических моделей расхождения геодезических точек на плоскости составили 0,5–1,0 мм, верхних точек 1–3 мм. Следует иметь в виду, что верхние точки попадают на края кадра и больше подвержены влиянию остаточной дисторсии. Для подсчета ожидаемых средних квадратических ошибок можно использовать формулы [2]. На основании их и с учетом того, что для определения элементов взаимного ориентирования на стереопарах было взято порядка 15–18 соответственных точек, получаем

  (9)

где  – обобщенная средняя квадратическая ошибка наведения на точки тест–объекта.

Упитывая совместное влияние ошибок измерения 0,3 пкс и остаточной дисторсии 0,5 пкс, можно принять = 0,6 пкс. При стереосъемке тест–объекта высота съемки и длина базиса были соответственно равны 1300 и 325 мм. Принимая  f   =  1800 пкс, по формулам (9) получаем:  = 0,7 мм; = 0,8 мм, что близко к реальным ошибкам. Таким образом, из эксперимента следует, что ошибки модели эквивалентны ошибкам измерений снимка (0,6 пкс). Следует отметить и возможное влияние на расхождения координат погрешностей в изготовлении макета, которые в нашем случае могли быть порядка 0,5 мм.

а б

Рис. 4. Перспективный снимок рельефного тест–объекта: а – исходный; б – после коррекции изображения

При лабораторном способе частичной калибровки изготовление тест–объекта максимально упрощается и сводится к нанесению меток на лист ватмана, а фокусное расстояние и высота съемки задаются приближенно. Причем степень этих приближений может быть весьма большой. Как показал опыт, ошибки в 20 – 30% вводимых величин практически не оказывают влияния на конечный результат.

Практическое значение частичная калибровка может получить при использовании цифровых камер в аэросъемочных работах, особенно для получения контурных планов в равнинных районах. В качестве примера можно привести аэросъемку, которую провела лаборатория фотогеологии геологического факультета МГУ в районах Чувашии, затопленных паводком в мае 2001 г., а также Куликова Поля и трасс трубопроводов в районе Уренгоя. Во всех случаях использовалась камера Nikon COOLPIX 950, по своим техническим характеристикам наиболее подходящая для данной цели, несмотря на значительную дисторсию. По снимкам, предварительно откорректированным по данным калибровки, составлялись обзорные фотосхемы с использованием системы Photoshop. Коррекция, которая проводилась с помощью системы ERDAS, позволила убрать искажения из–за дисторсии, обеспечив хорошую сходимость на стыках снимков. На основании этого материала и геодезического обоснования могут быть составлены полноценные фотопланы. Та же камера использовалась нами и в ближней стереосъемке. Задачей была съемка внутренней части производственного помещения с высоты 6,8м при колебаниях превышений до 1,8м. Наличие геодезического обосновании позволили создать трехмерную модель в заданной системе координат и фрагменты плана с отметками высот точек. Расхождения на опорных и контрольных точках не превысили 1 см в плане и 1,5 см по высоте, что отвечает теоретическим расчетам и требованиям съемки.

Таким образом, можно констатировать, что применение относительно недорогих цифровых камер с последующей фотограмметрической обработкой снимков возможно даже при значительной дисторсии при условии их калибровки и корректирования получаемых изображений.

Список литературы

1.Гельман Р.Н. Точность измерений по снимкам, полученным неметрической камерой // Геодезия и картография. – 1982 – №7. – С. 29–32

2.Гельман Р.Н. Еще об оценке точности одиночной фотограмметрической модели // Геодезия и картография. – 2000 – №12. – С. 19–23.

3.Елисеев С.В. Геодезические инструменты и приборы. – М.: Недра, 1973. – 390с.

4.Лаврова Н.П., Стеценко А.Ф. Аэрофотосъемка, аэрофотосъемочное оборудование. – М.: Недра, 1984. – 220с.

5.Stereo–comparator  для  Windows v.1.0 //  ГИС – обозрение . – 1998 – №1. – С . 11