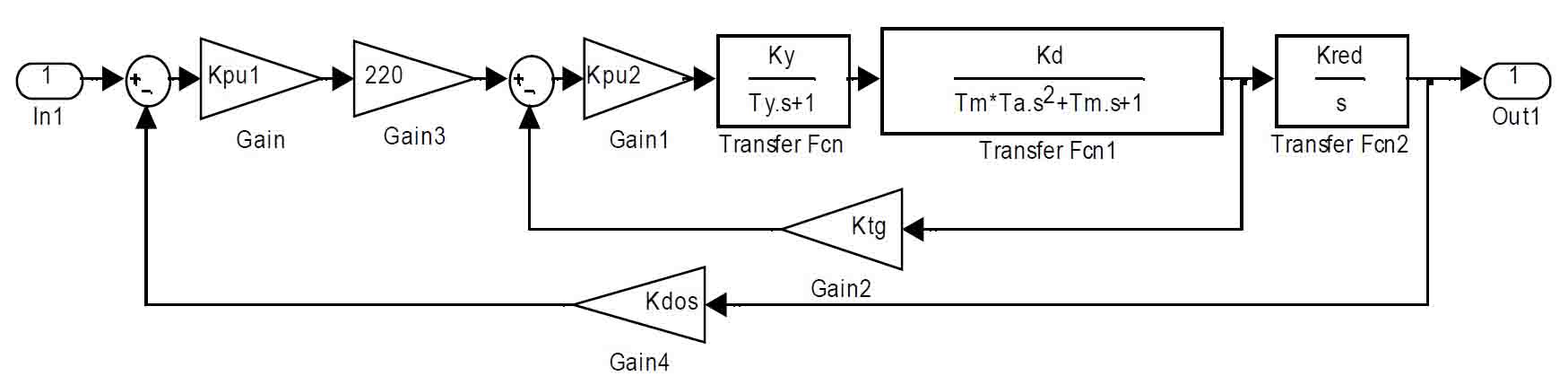
Рисунок 1 – Структурная схема двухконтурной электромеханической следящей системы
Автор:А. П. Харченко, Ю. С. Слепокуров, П. А. Аверьянов
Источник: Научная электронная библиотека Киберленинка
Для приводов манипулятора промышленного робота актуально повышение быстродействия в 2-3 раза при сохранении плавности перемещения захватного устройства (ЗУ). Плавность перемещения ЗУ обеспечивается получением апериодической 2-го порядка переходной характеристики. Приводы звеньев манипулятора робота строятся однотипно как многоконтурные автоматические системы с подчиненным регулированием. Существует несколько способов обеспечения заданных динамических показателей качества регулирования. Наиболее часто используются корректирующие устройства (КУ), ПИ-регуляторы и в последнее время перспективно применение модального регулятора (МР). Не исследованы возможности современных методов проектирования автоматических систем с обратной связью при их практической реализации. Сравнительный анализ способов повышения быстродействия при вариации их параметров выявил допустимые границы изменения времени регулирования и перерегулирования переходной характеристики при условии сохранения ее вида. Использование ПИ-регуляторов для получения заданных параметров качества регулирования ограничивается взаимной зависимостью времени регулирования и перерегулирования. Произвольное изменение коэффициентов МР выявило нелинейную функциональную зависимость времени регулирования и перерегулирования от их значения. При сравнении чувствительности параметров качества регулирования по переходной характеристике к 50% изменению постоянных времени КУ и 50% изменению коэффициентов МР время регулирования и перерегулирования последнего не изменяется. Изменение на 50% постоянных времени Т в передаточной функции КУ влияет на перерегулирование, и переходной процесс превращается в колебательный. При этом быстродействие САУ при перерегулировании не более (0.04-0.05) % с МР повышается в 3 раза, а быстродействие САУ с КУ – в 1,8 раз.
Результаты исследований позволяют сделать вывод о том, что применение МР обеспечивает наибольшее быстродействие следящей системы и заданных показателей качества управления. Использование МР, в отличие от классических регуляторов, не вносит дополнительную инерционность в следящую систему. Вместе с этим в литературных источниках, где описывается МР, отмечаются некоторые недостатки применения МР, которые ограничивают его практическое применение. Поиск путей устранения этих недостатков является целью представленных и последующих исследований следящей системы с МР
Ключевые слова: электромеханическая следящая система, структурная схема, модальный регулятор, переходная характеристика
Электромеханическая следящая система или система автоматического управления положением представляет собой систему подчиненного регулирования, управляющую перемещением звеньев манипулятора промышленного робота и обеспечивающую1 стабилизацию положения захватного устройства манипулятора (исполнительного органа) промышленного робота относительно некоторой базовой системы координат в пространстве расположения манипулятора.
Электромеханическая следящая система обеспечивает как линейное, так и угловое перемещение звеньев манипулятора.
Среда Matlab позволяет, используя визуальные блоки и передаточные функции элементов, программно и аппаратно реализовать структурную схему электромеханической следящей системы.
Структурная схема двухконтурной электромеханической следящей системы управления руки промышленного робота [1] состоит из системы автоматического регулирования скорости (САР) скорости и следящей системы (СС) – рис.1.

Рисунок 1 – Структурная схема двухконтурной электромеханической следящей системы
Передаточная функция СС выражается
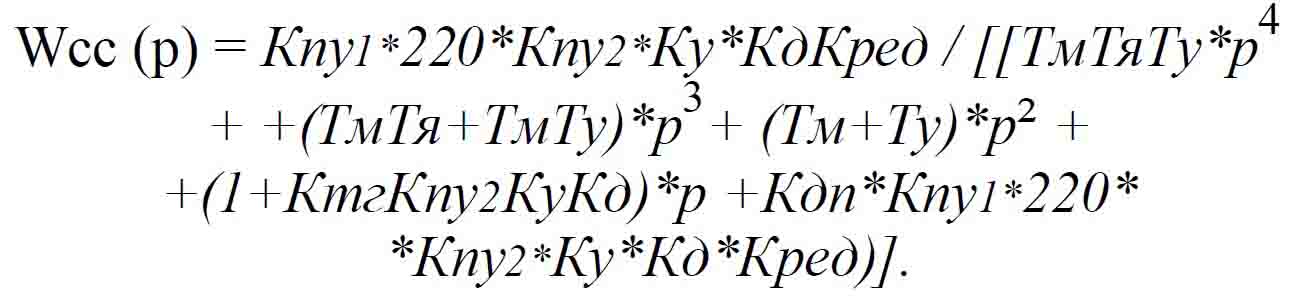
Дифференциальное уравнение СС выражается
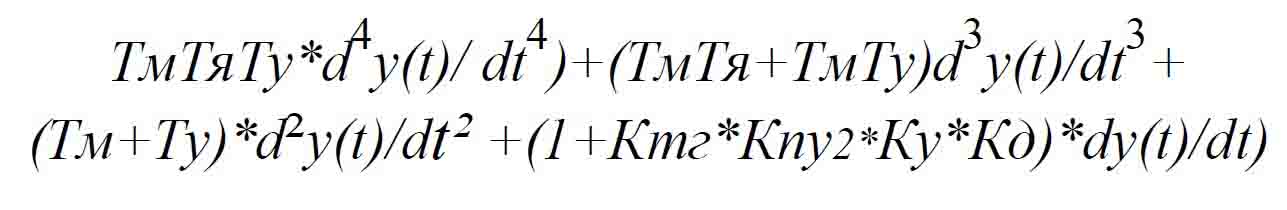

Более компактной формой математического описания СС является уравнения в векторно-матричной форме [2]

где А,В,С,D – матрицы.
При моделировании использованы параметры двигателя постоянного тока LSK 1124M французской компании “Leroy – Somer” мощностью 3.5 кВт. Выбраны датчик обратной связи по положению burster 8820 EN, который имеет измерительный диапазон 350º ± 4º с разрешением 0.01º и тахогенератор ТГП-1А – коллекторный постоянного тока с зубцовым ротором с крутизной 5 мВ/(об/мин).
СС предварительно настраивается по условиям эксплуатации с П-регуляторами.
Из условий работы САР скорости следует, что при подаче на вход системы Uн = 220В двигатель разгоняется до номинальной скорости – nном. Изменяется Кпу2. По условиям работы переходная характеристика СС быть апериодической 2-го порядка. Изменяется Кпу1.
На рис. 2 представлены переходные характеристики следящей системы при изменении Кпу1.
Уменьшение коэффициента Кпу1 сохраняет форму апериодической переходной характеристики 2-го порядка, но время регулирования возрастает.
Увеличение коэффициента Кпу1 изменяет форму апериодической переходной характеристики 2-го порядка на колебательную, но время регулирования уменьшается.
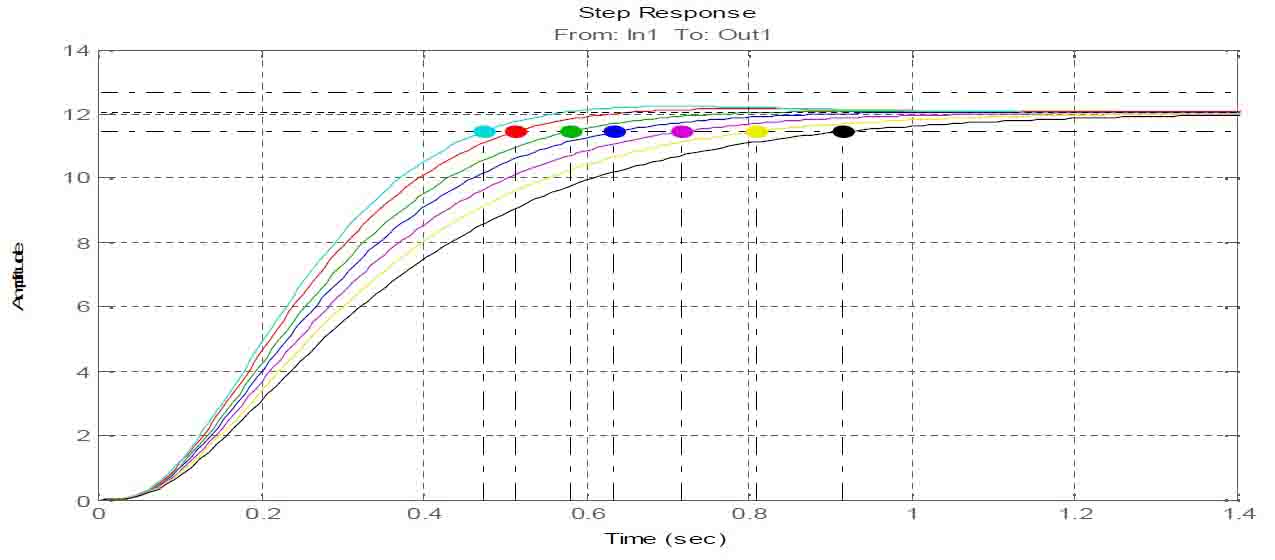
Рисунок 2 – Переходные характеристики СС при изменении Кпу1
Наименьшее время регулирования имеет переходная характеристика СС с перерегулированием не более 0.05% при заданном допустимом отклонении Δ = ± 0.05*hуст.
Особенностью СС является и то, что различные углы задания ее переходная характеристика отрабатывает с одним и тем же временем регулирования – рис. 3.

Рисунок 3 – Переходная характеристика СС при отработке различных углов задания
При сохранении формы переходной характеристики СС уменьшение времени регулирования при использовании П-регулятора не возможно, так как существует зависимость времени регулирования и перерегулирования от значения коэффициента регулятора Кпу1.
Уменьшение времени регулирования СС может быть получено при использовании модального регулятора (МР).
Синтез заданных показателей качества регулирования в среде Matlab с использованием МР требует векторно- матричного уравнения или уравнения пространства состояний СС.
Особенностью исследования систем автоматического управления при задании структурных схем в области Simulink является то, что при исследовании системы в рабочей области Matlab матрицы А, В, С и D не соответствуют матрицам исходной системы.
Получены матрицы векторно- матричного уравнения [3] СС:

Матрица строка коэффициентов МР СС записывается: К = [К1 К2 К3 К4].
Уравнение СС с МР представляется dх/dt = ( А1–В1*К )*х + В1*V,
где V – скалярный вход, как сумма входного сигнала и выходного сигнала МР.
В то время как динамические свойства исходной СС определяются матрицей А1, динамические свойства СС с МР определяются матрицей А = А1–В1*К

Первой особенностью при проектировании СС с МР является изменение амплитуды всех составляющих вектора состояний, то есть при повышении быстродействия амплитуды составляющих вектора состояний превышают допустимые значения таких величин, как скорость, ток и напряжение двигателя.
Второй особенностью использования МР является чувствительность переходной характеристики к изменению коэффициентов К1, К2, К3 и К4.
Оценим изменение коэффициентов К1, К2, К3 (коэффициент К4 не влияет) на относительное изменение перерегулирования ?/?о и относительное изменение времени регулирования tp/tpo.
Результаты исследований СС приведены в табл. 1-3.
Таблица 1 Влияние коэффициента К1 на исходный апериодический процесс
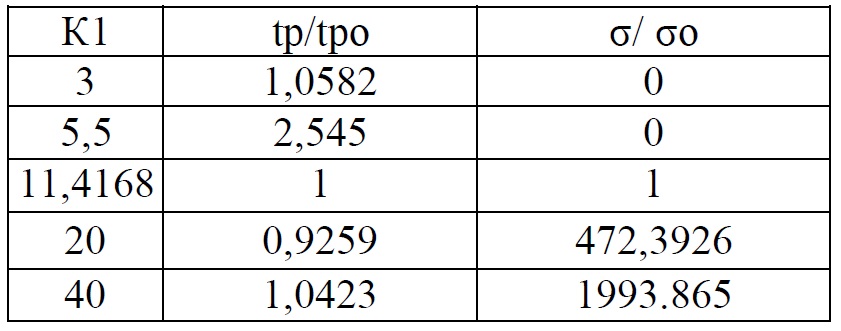
Таблица 2 Влияние коэффициента К2 на исходный апериодический процесс
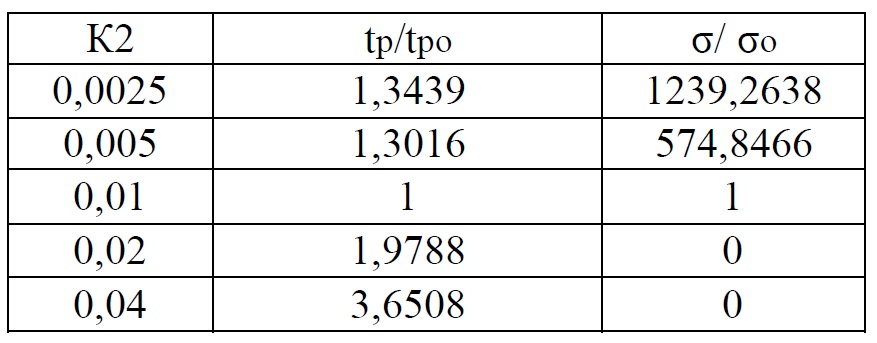
Таблица 3 Влияние коэффициента К3 на исходный апериодический процесс
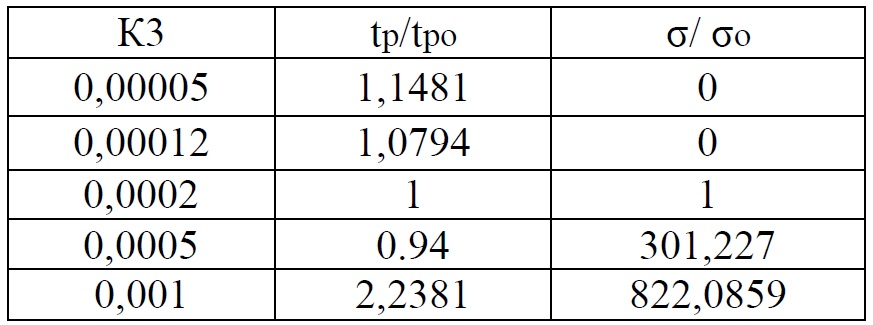
По результатам исследований построены графики зависимостей tp/tpo = F (К1), tp/tpo = F (К2), tp/tpo = F (К3) – рис. 4-6.

Рисунок 4 – Зависимость tp/tpo = F (К1)
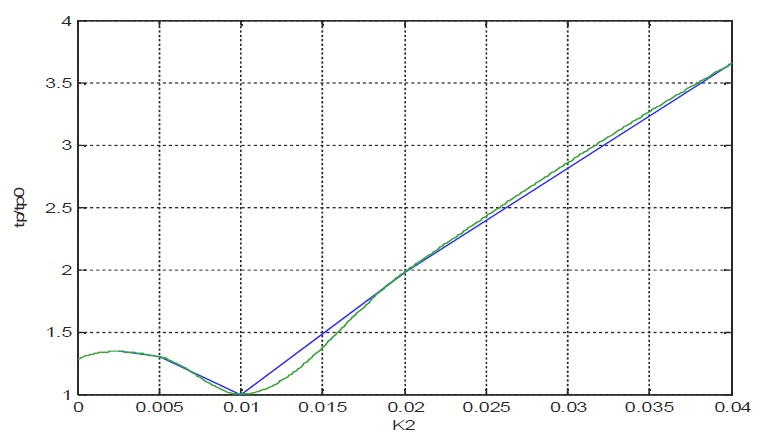
Рисунок 5 – Зависимость tp/tpo = F (К2)
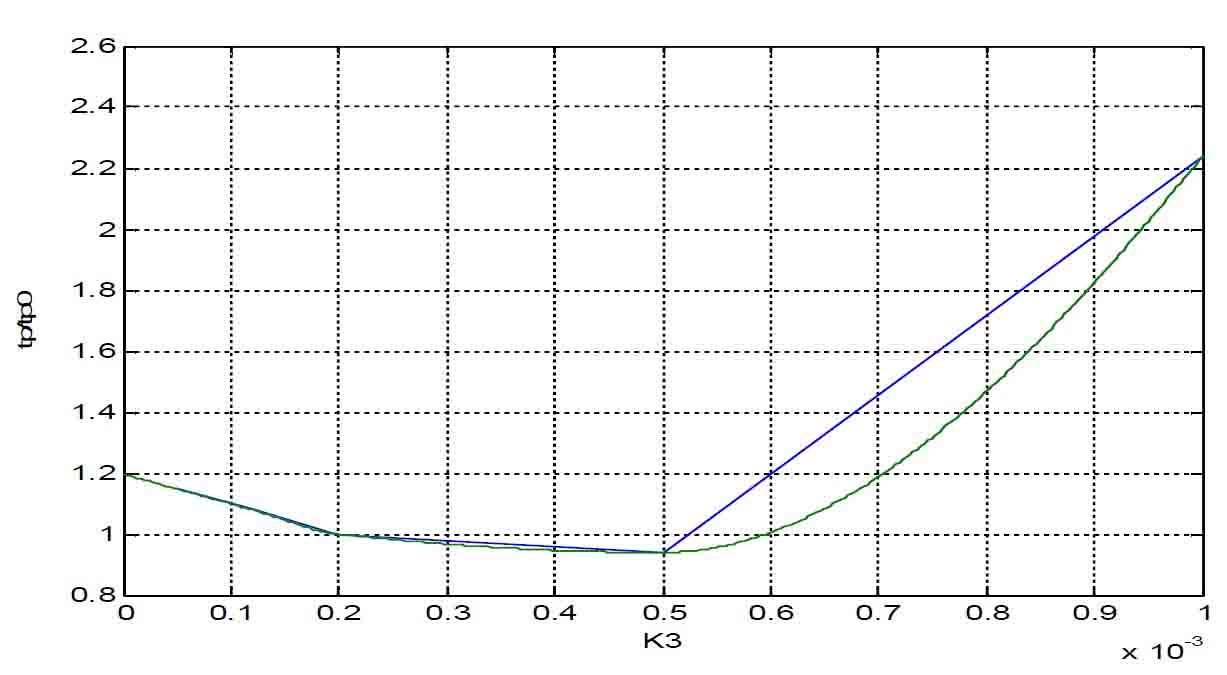
Рисунок 6 – Зависимость tp/tpo = F (К3)
Графики зависимостей σ/σo = F (К1), σ/σo = F (К2), σ/σo = F (К3) представлены на рис. 7-9. При этом σo = 0.05% – перегулирование переходного процесса в исходной структурной схеме с МР, а σ – перегулирование переходного процесса в структурной схеме с доступом к переменным состояний с измененными значениями параметров МР.

Рисунок 7 – График зависимости σ/σo = F (К1)

Рисунок 8 – График зависимости σ/σo = F (К2)
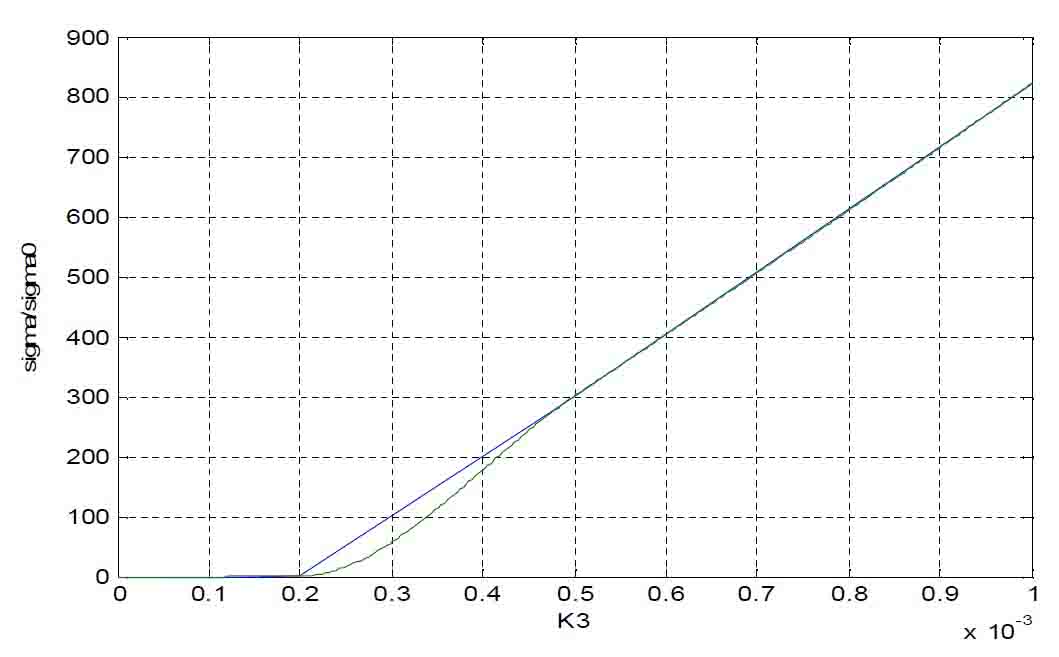
Рисунок 9 – График зависимости σ/σo = F (К3)
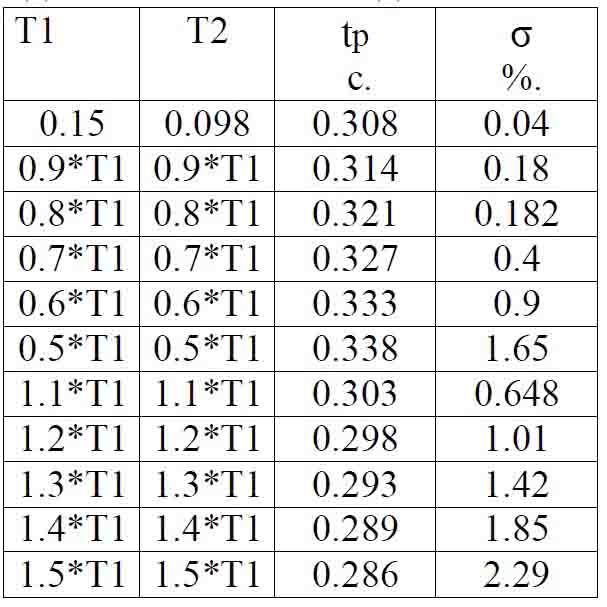
Сравним чувствительность параметров переходной характеристики, (время регулирования и перерегулирование) СС с последовательным корректирующим устройством (КУ) в виде форсирующего и апериодического типовых звеньев с постоянными времени Т1 и Т2 и чувствительность параметров переходной характеристики СС с МР к коэффициентам К1, К2 ,К3 и К4.
На рис. 10 изображена схема исследования СС с МР и наблюдателем. Наблюдатель восстанавливает недостающие для реализации обратных связей (ОС) переменные Х3 и Х4.
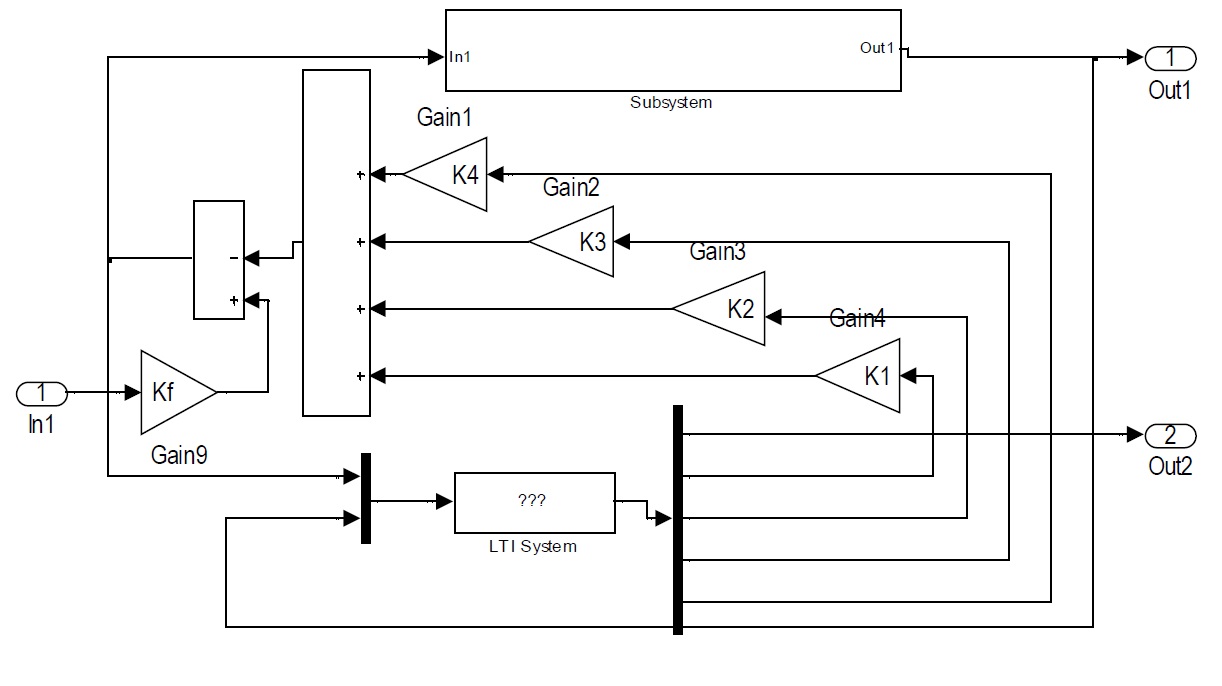
Рисунок 10 – Схема исследования СС с МР и наблюдателем
Коэффициент Kf введен для компенсации изменения амплитуды входного сигнала.
Время регулирования переходной характеристики исходной СС tp = 0.582 с.
В табл. 4 представлены исследования с МР, а в табл. 5 исследования с последовательным КУ.
Применение МР, при заданном перегулировании σ = (0.04-0.05)%, соответствует повышению быстродействия в 3 раза.
Применение последовательного КУ , при заданном перерегулировании (0.04-0.05)%, соответствует повышению быстродействия в 1.8 раза.
Таблица 4 – Исследования СС с МР
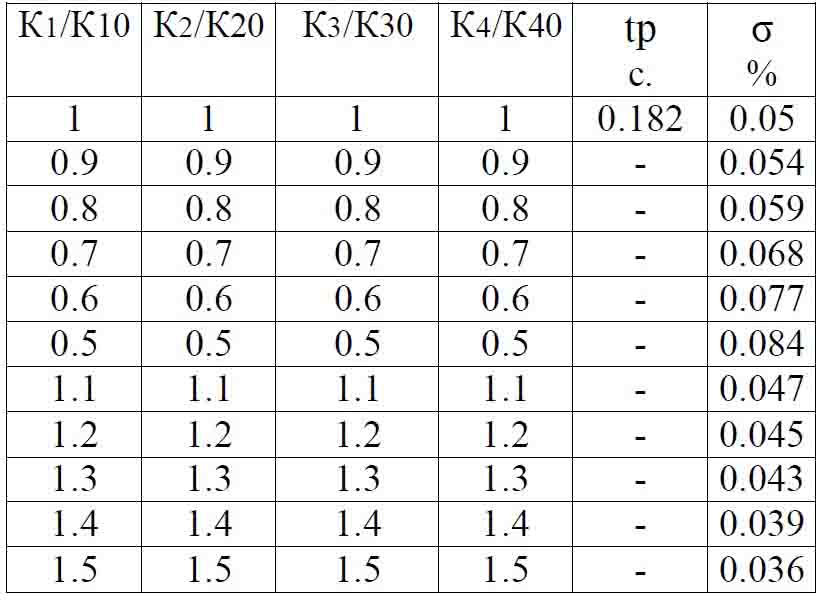
Таблица 5 – Исследование СС с последовательным КУ
Таким образом, исследования СС с МР доказали преимущество МР перед классическими способами проектирования.