
Рисунок 1 – Основная схема токового шунта в электроприводах
Автор: A. Anuchin, D. Surnin, M. Lashkevich
Перевод: Адарченко А. В.
Источник: Закрытая научная библиотека ieeexplore.ieee.org
Рассматривается точность измерения тока с помощью шунтового датчика в частотно-регулируемом электроприводе с использованием дельта-сигма модуляции. Измерение тока с помощью резистивных шунтов становится все более распространенным благодаря появлению гальванически развязанных микросхем дельта-сигма преобразователей (модуляторов). Данное решение оказывается дешевле датчиков тока на эффекте Холла компенсационного типа и уже успешно применяется в некоторых промышленных электроприводах. Исследуется точность получаемого результата после демодуляции в микроконтроллере. Путем моделирования получены зависимости максимальной погрешности от коэффициента передискретизации (oversampling ratio), типа цифрового фильтра и относительного значения входного сигнала.
В течении многих лет датчики Холла с замкнутым контуром были самыми часто используемыми датчиками при измерении тока в высокопроизводительных силовых электронных системах. Их преимущества хорошо известны:
Основным недостатком является высокая цена датчика; и это заставляет исследователей и проектировщиков искать другие возможные решения для измерения тока. Существуют следующие:
На датчики тока с разомкнутым контуром влияют внешние магнитные поля, подобные тем, которые создается током других фаз того же силового преобразователя. Этот эффект можно принять с учетом точной калибровки алгоритма измерения, учитывая другие токи, протекающие в системе.
Токовые шунты популярны в маломощном оборудовании, но для мощных промышленных преобразователей и электрических приводов с током, превышающим 50 А выходного тока они не используются из-за отсутствия удобного решения для осуществления гальванической развязки. Решением может быть последовательный АЦП, на который влияет задержка при передаче данных через оптосоединительное устройство. Существующие ныне преобразователи напряжения имеют низкую пропускную способность при высокой частоте и неприемлемую задержку измерения сигналов низкочастотной модуляции.
Следующий шаг произошел, когда специальные преобразователи напряжения, основанные на дельта-сигма модуляции появились вместе с поддержкой специального периферийного устройства с демодулятором и цифровыми фильтрами, встроенными в современные микроконтроллеры. Подобные микросхема AMC1305 от Texas Instruments измеряет падение напряжения в шунтирующем резисторе и производит дельта-сигма-модуляцию потока данных. Поток данных 10 или 20 МГц имеет время и сигнал данных и нуждается только в двух цифровых изоляционных устройствах; и только в одном, если используется Манчестерское кодирование.
Производители, такие как Semikron, начали производить мощные модули со встроенными токовыми шунтами на выходе схемы. Texas Instruments предлагает серию дельта-сигма модуляторов и микроконтроллеров со встроенными демодуляторами. Все эти компоненты вместе могут заменить датчики тока на эффекте Холла с замкнутым контуром, экономя приблизительно 30 долларов США за каждый датчик (для номинального тока датчика 200 А).
В то время как исследователи начали разработку таких систем с использованием измерения дельта-сигма-тока, и изучили точность текущих шунтовых модулей, не появилось четкого понимания точности данных, которые могут быть достигнуты путем извлечения из модулированного потока битов. Единственные документы, которые дают некоторые зависимости между соотношением передискретизации, типа фильтра и пропускной способности предоставляются производителями и содержат неправильные ожидания относительно эффективного количества бит. Помимо этого, пропускную способность и точность часто путают.
Целью данной работы является исследование точности и максимальной погрешности измерения токовым шунтом с использованием идеального дельта-сигма-модулятора. Это будет сделано в отношении частоты передискретизации (OSR) и типа используемого фильтра. Достигнутые результаты, будут сравниваться с обычным 12-разрядным АЦП, который обычно используется в современных силовых преобразователях и электрических приводах. Сравнение будет проводиться с точки зрения точности и частоты дискретизации, необходимой для высокопроизводительного контроля системы с быстрой реакцией тока.
1. Шунт
Шунт последовательно помещается в цепь с протекающим током (см. рис. 1). Обычно используются два варианта: шунты на 50 мВ и на 250 мВ. Эти падения напряжения заданы для максимального тока, который может протекать через шунт, и обычно они в два раза превышают номинальное значение. Более высокое падение напряжения приводит к более высоким потерям в системе. Для номинального тока 400 А рассеиваемая мощность шунта на одной фазе – 10 Вт и 25 Вт для шунтов 50 мВ и 250 мВ соответственно. Это оказывает некоторое влияние на тепловой режим хотя снижение общей эффективности в любом случае пренебрегается.

Рисунок 1 – Основная схема токового шунта в электроприводах
2. Дельта-сигма модулятор
Дельта-сигма-модулятор подключается непосредственно к токовому шунту. Необходимо изолировать источники питания – от первичной и вторичной цепей. Вторичная цепь питания может быть использована из цепи питания микроконтроллера, в то время как потенциал первичной цепи сглаживается во время коммутации выключателей питания силового модуля. Это питание может быть гальванически подключено к источнику питания привода верхней стороны переключателя.
Микросхемы, такие как AMC1303, содержат, коммутируемый конденсатор второго порядка, опережающего ΔΣ-модулятор, который создает битовый поток с информацией о протекающем токе. В таблицах данных представлены обычно неточные структуры модуляторов, поскольку им не хватает коэффициентов усиления для блоков интегратора, что делает структуру неработоспособной. Структура для этого исследования была взята из [11] и показана на рисунке 2. Реализация обоих интеграторов в дискретную форму делает эту структуру временной инвариантной независимо от частоты модуляции.

Рисунок 2 – Структурная схема дельта-сигма модулятора второго порядка
3. Демодуляция битового потока
Демодуляцию битового потока можно выполнить посредством специального периферийного устройства современного микроконтроллера или с использованием ППВМ (программируемая пользователем вентильная матрица). Битовый поток должен быть отфильтрован с помощью фильтра низких частот и обычного варианта – Sinc-фильтра [12] разных порядков. Вообще, Sinc-фильтр первого порядка фильтр скользящей средней; и он может быть представлен IIR [9] или FIR, в то время как результат операции остается таким же:

где z – оператор сдвига по времени, N – избыточная выборка (OSR) или количество бит в потоке, которые используются в фильтре. Абсолютная ошибка сигнала, восстанавливаемого таким фильтром, это обратное значение количества обработанных бит:
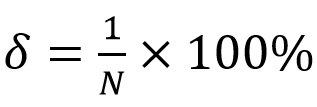
Информация о значении сигнала представлена не только средним значением битов в реализованном битовом потоке. Скорость переключения битов добавляет дополнительную информацию, которую можно извлечь, применяя фильтр высокого порядка. Самый простой способ реализации фильтра второго или третьего порядка – это последовательное соединение трех фильтров первого порядка. Одновременная работа Sinc, Sinc2 и Sinc3 с коэффициентом избыточной дискретизации 8 бит представлена на рис.3. Первоначально входной сигнал установлен на 60% от всего диапазона и в середине эксперимента ввод сигнал изменяется до 90% диапазона.

Рисунок 3 – Работа фильтров Sinc, Sinc2 и Sinc3 для OSR равна 8 (верхний график: красный – входной сигнал, желтый – выходной сигнал фильтра Sinc, фиолетовый – выходной сигнал фильтра Sinc2, синий – выход фильтра Sinc3; нижний график: битовый поток)
4. Точность измерения
Анализ переходного процесса показывает, что реализация фильтра высокого порядка увеличивает разрешение выходного сигнала, в то время как точность тоже становится лучше. Мы видим, что точность выходного сигнала зависит от частоты битового потока. Эта частота, в свою очередь, зависит от уровня входного сигнала относительно его максимального и минимального значений.
Чтобы повысить точность измерения тока, следует использовать более высокий коэффициент передискретизации. Увеличение коэффициента передискретизации вместе с цифровой фильтрацией приводит к росту времени измерения. Более длительная продолжительность измерения нежелательна для системы управления из-за увеличения задержки в текущей обратной связи. Следовательно, баланс между точностью и продолжительностью измерения тока необходим для достижения максимальной производительности текущего контура управления.
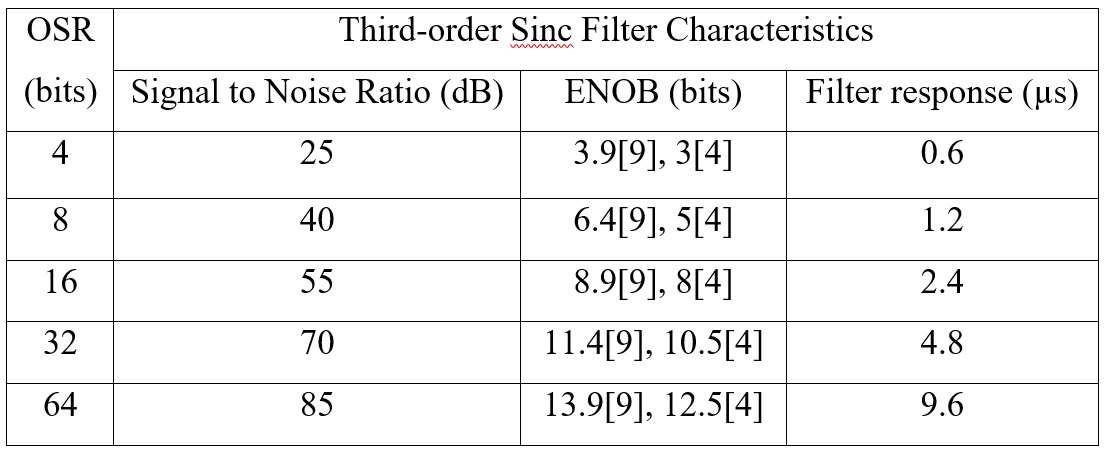
В [9] точность представлена эффективным числом битов (ENOB) для каждой конфигурации типа OSR и типа фильтра. Параметры для фильтра Sinc3 показаны в таблице 1. Длительность текущего измерения или время отклика фильтра для 20 МГц часов. Согласно таблице 1, приемлемая ЛАРН значение лежит между 16 и 32. Обычно 12-разрядный АЦП имеет от 10 до 11 ENOB; поэтому нет оснований увеличивать ЛАРН с той же точностью петли тока. Но эти данные различаются из приведенного в [4].
Поскольку сложно оценить эффективное количество битов из-за того, что оно зависит не только от количества бито, но и от скорости коммутации битов в битовом потоке, проверка данных из таблицы 1 может быть выполнена с использованием некоторого крайнего случая. Рассмотрим ситуацию, когда фильтр Sinc3 с OSR равен 16 находится в действии; и входной сигнал составляет 1/49 от общего диапазона что соответствует одному биту ENOB. Это означает, что модулированный сигнал имеет 1 положительный импульс и 48 отрицательных импульсов. Могут быть две возможные ситуации во время измерения. Во-первых, когда один положительный бит встречается вместе с 47 отрицательными битами, а измеренное значение не равно нулю. А второй вариант заключается в том, что происходит 48 отрицательных импульсов во время измерения, а измеренный сигнал равен нулю. Поэтому если, максимальная ошибка составляет 1/49 от всего диапазона или 2%, то от ENOB она должна составлять 0,4% в соответствии с [4] и 0,2% согласно [9]. Это расхождение должно быть исследовано средствами модели дельта-сигма-модуляции и демодуляции.
Талица 1. Характеристики фильтра Sinc 3
Модель состоит из источника входного сигнала, второго порядка дельта-сигма-модулятора (см. рисунок 4а) и последовательного Sinc фильтра. В результате первый фильтр Sinc является простым перемещением в среднем, он не использует дополнительную информацию при переключении скорости битового потока. Следовательно, выход Sinc фильтр первого порядка не следует рассматривать. Сравнение должно быть выполнено между выходами Sinc2 и Sinc3 для одного и того же измерения времени. Выход фильтра должен сравниваться с входным сигналом, что помогает оценить ошибку как функцию входного сигнала. Входной сигнал изменяется от среднего к максимальному. Проверять его во всем диапазоне нет смыслу, поскольку операция симметрична. Модель была реализована в Simulink MATLAB; ее структура показана на рисунке 4d. Модель фильтра представлена на рисунке 4b. Пиковый детектор ошибок (см. рисунок 4c) собирает максимальную ошибку во время 100 измерений.
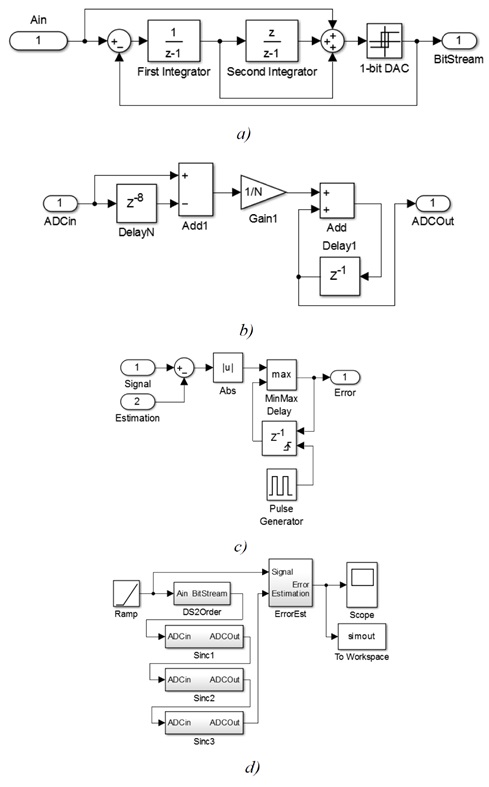
Рисунок 4 – Модель экспериментальной установки (a – подсистема дельта-сигма модулятора второго порядка (DS2Order); b – подсистема Sinc фильтра (Sinc1, Sinc2, Sinc3); c – подсистема детектора пиковых ошибок (ErrorEst); d – модель экспериментальной установки)
Первый эксперимент был выполнен с OSR равным 8 и Sinc3 (см. рис.5a) и OSR равны 12 и Sinc2 фильтр (см. рис. 5b). В обоих случаях 8 * 3 и 12 * 2 битов из битового потока обрабатывались. Результаты показывают, что в обоих случаях максимальная ошибка достигает наивысших значений, когда входной сигнал приближается к своему максимуму. Характеристика Sinc2 более плоская в области от 0 до 75%, а Sinc3 начинает расти после 50% величины сигнала.
При более длительном измерении точность увеличивается. Максимальная ошибка для метода Sinc3 (см. рис. 6a) теперь ниже чем для Sinc2 (см. рис.6b) и имеет 0,25% при нулевом входном сигнале и увеличивается от 0,5% до 75% от максимального значения. И то и другое измерение соответствует приблизительно 8 эффективным битам, в то время как точность измерения с помощью фильтра Sinc2 ниже в среднем.
Увеличивая коэффициент передискретизации до 32 в случае Sinc3 фильтра, максимальная погрешность составляет 0,05% для диапазона от 0 до 50% входного сигнала (см. рис. 7а). Это соответствует 11 эффективным битам. Результаты для фильтра Sinc2 с той же продолжительностью измерения хуже (см. рис. 7b).

Рисунок 5 – Ошибки для a) Фильтр OSR = 8 и Sinc3 фильтр, b) Фильтр OSR = 12 и Sinc2 фильтр

Рисунок 6 – Ошибки для a) Фильтр OSR = 16 и Sinc3 фильтр, b) Фильтр OSR = 24 и Sin2 фильтр
Увеличение ошибки в области высоких входных сигналов не оказывает реального влияния на производительность контроля замкнутого контура. Эти значения доступны только при перегрузке условий, когда требования к качеству регулирования не применимы.
Измерение токовым шунтом с использованием дельта-сигма модуляция – это дешевый и точный метод измерения в системах управления. Он обеспечивает более высокую точность при малых входных сигналах, а при перегрузке точность условий снижается. Еще одно преимущество этого метода – это его иммунитет к шуму коммутации в силе конвертера. Время измерения сравнимо с обычными АЦП и находится в диапазоне между 2.4 и 4.8 мкс для того же разрешения.
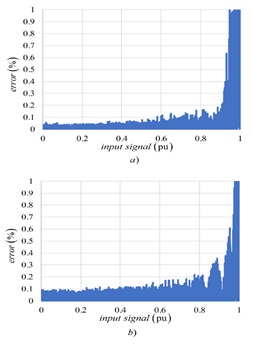
Рисунок 7 – Ошибки для a) Фильтра OSR = 32 и Sinc3, b) Фильтра OSR = 48 и Sinc2