Проектирование дробной системы ПИД–регулирования для бесколлекторного двигателя на основе FPGA
Авторы: Fan Zhang, Zhuangju Li
Перевод: Е.А. Бондаренко
Источник: 2018 Chinese Control And Decision Conference (CCDC) – 9–11 June 2018
Аннотация
В этой статье была разработана система бесконтактного управления двигателем постоянного тока, основанная на программируемой вентильной матрице (FPGA). Система состоит из двух частей: FPGA и периферийных цепей. FPGA как управляющее ядро всей цепи, через аппаратный язык программирования VerilogHDL, программирует внутреннюю аппаратную схемы FPGA для завершения дробного алгоритма ПИД–регулирования, котоный основанный на дробном режиме управления ПИД–регулятором, для достижения соответствующего регулятора выходного сигнала ШИМ. Результаты моделирования показывают, что ПИД-контроллер дробного порядка на основе FPGA (ПЛИС) имеет преимущественно простую структуру, гибкое управление и большую помехоустойчивость, а также отвечает фактическим требованиям регулирования скорости двигателя. Ключевые слова: Программируемый массив затворов, бесщеточный двигатель постоянного тока, ШИМ, дробный ПИД.
1 Введение
Двигатель постоянного тока с небольшими размерами, малым весом, высокой эффективностью, высоким крутящим моментом и низким энергопотреблением и другими преимуществами широко используются в аэрокосмической, авиационной, автомобильной, медицинской технике и машинах с ЧПУ и других областях [1]. Однако с развитием электронных технологии, люди выдвинули более высокие требования к стабильности и точности BLDC (бесколлекторных) моторов. Традиционная система управления двигателем постоянного тока с низко интегрируема, больше по габаритам, более уязвима для внешней среды, её трудно отлаживать. Традиционный алгоритм ПИД–регулирования параметров относительно ступенчатый, точность управления не высокая [2–4]. Управление двигателем на основе микроконтроллера не может использовать продвинутые теории управления для выполнения более эффективных алгоритмов управления, таких как внутренняя структура и вычислительные возможности. Высокопроизводительные цифровые процессоры имеют алгоритмический но их внешние цепи сложны и восприимчивы к внешним помехам [5].
Система управления высокоточным бесколлекторным двигателем постоянного тока на FPGA, основанная на современных требованиях производства, позволяет разработчикам схем создать, осмыслить, промоделировать, тестировать и проверять их с помощью компьютерных платформ разработки. Аппаратное обеспечение FPGA, встроенное в аппаратный программный язык может сэкономить много аналогичного оборудования. Он объединяет устаревшие эементы поверхностной пайки в элементы на чип–уровне, что снижает энергопотреблене и циклы системных исследований, повышает надежность, упрощает модернизацию и обновляется онлайн. Параллельная обработка данных ПЛИС может значительно повысить эффективность работы системы. Поэтому использование FPGA для управления двигателем постоянного тока является актуальным. Благодаря экспериментальной проверке выявлено, что система эффективно подавляет пульсации момента, сокращают время регулирования и улучшает стабильность системы.
2 Структура оборудования системы управления бесколлекторным двигателем
Схема аппаратного управления бесколлекторным двигателем в основном состоит из контроллера ПЛИС, схемы питания, цепи регулирования напряжения, цепи обнаружения пересечения нуля. Общая система аппаратного оборудования показана на рисунке 1. FPGA контроллер использует форму ШИМ для управления выходным сигналом и питает трехфазную схему полного моста инвертора, который ведет контроль за фазой двигателя. Скорость двигателя определяется путем косвенного вычисления сигнала обнаружения положения. Рабочий цикл ШИМ контролируется с помощью отрицательной обратной связи что позволяет достигать точного контроля скорости ДПТ через определение тока и положение сигнала обнаружения.
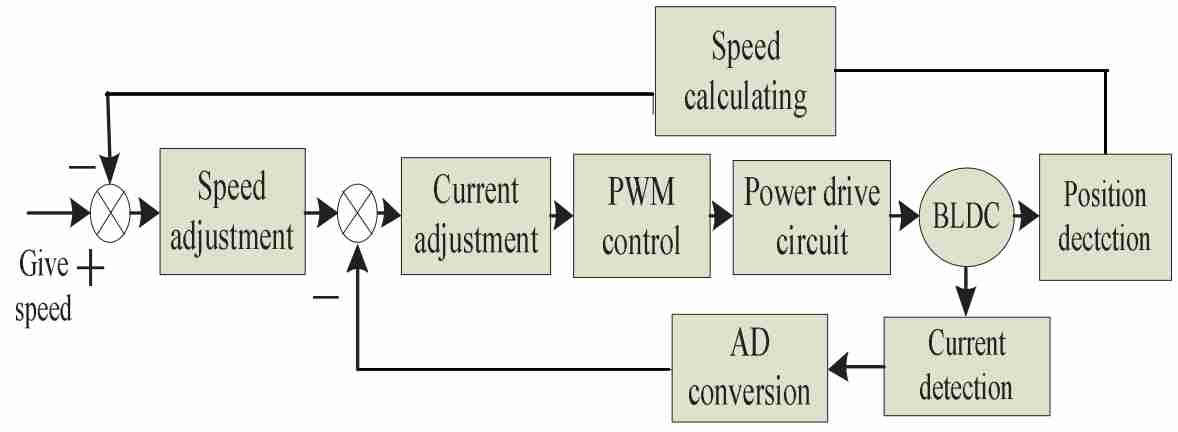
Рисунок 1 – Структурная схема устройства по управлению бесколлекторным двигателем
3 Дробное исчисление и система ПИД–регулирования
Основное различие между исчислением дробного порядка и исчисление целочисленного порядка состоит в том, что порядок дробных исчисление произвольно выбирается из действительных чисел и комплексных чисел [6]. Оператор дробного исчисления определяется следующим образом:
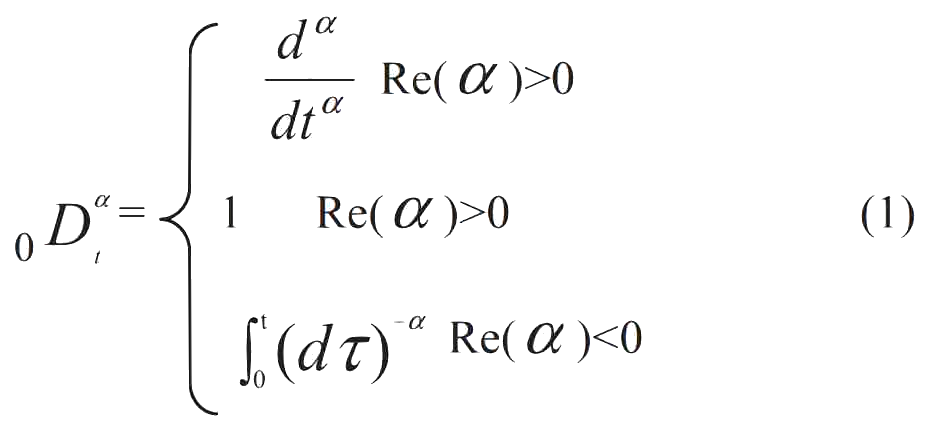
В приведенном выше уравнении t и 0 являются верхними и нижними пределами дифференциала и интеграла, а α – произвольное комплексное число, τ является интегральной переменной. Re(α) – реальная часть интегральной переменной. Через введение оператора, дифференциал и интеграл принимают унифицированное выражение. Когда Re(α)>0, он представляет дробный дифференциальный оператор, а когда Re(α)<0, он представляет соответствующий интегральный оператор. Поэтому интегральный и дифференциальные операторы можно рассматривать как операторы обсуждения. Дробное исчисление имеет несколько разных определений. В этой статье был использован Метод Грюнвальда–Летникова. Ниже приводится краткое введение в метод Грюнвальд–Летникова [7]. Число α является порядком исчесления функции f(t) и определяется как:
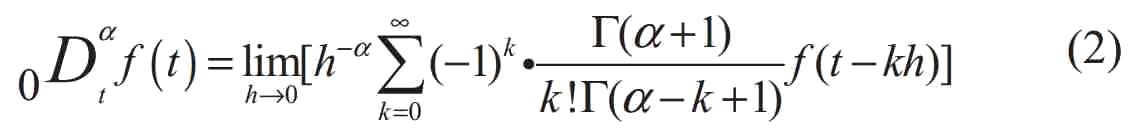
В уравнении α> 0, Γ (·) – эйлеровая гамма функции. Важно понимать, что дробная производная в определенной точке функции f(t), связана с значением функции между начальной точкой и этой точкой, то есть является машинной памятью, которая не совпадает с традиционной формой исчисления.
ПИД–регулятор дробного порядка вводит дифференциальный порядок μ и интегральный порядок λ на основе целочисленного порядка, который увеличивает количество настраиваемых параметров и делает его более гибким. Управляющее воздействие также было оптимизировано, и соответствующая блок–схема показана на рисунке 2.
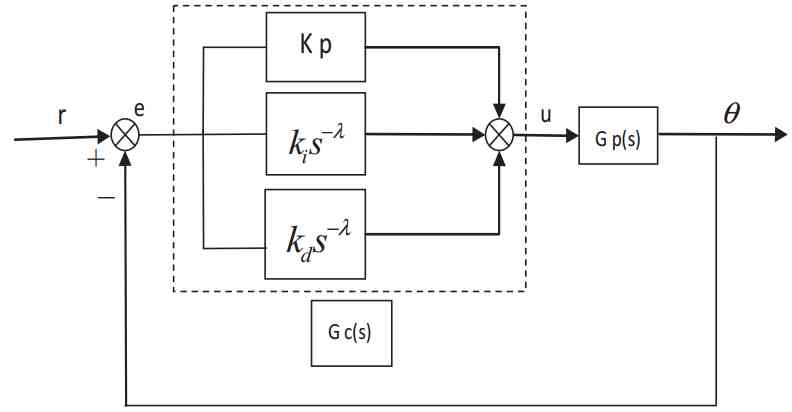
Рисунок 2 – Блок–схема дробной системы ПИД–регулятора
Передаточная функция дробного ПИД–регулятора представлена следующим обазом [8]:
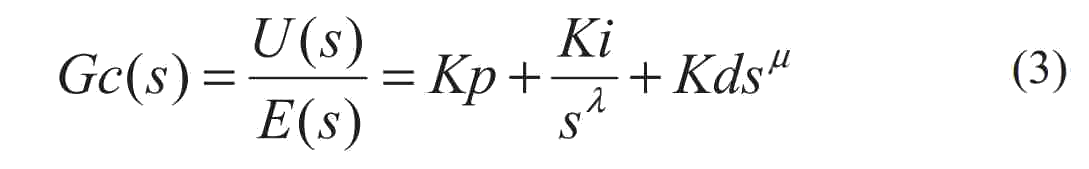
Выводимое выражение во временной области:
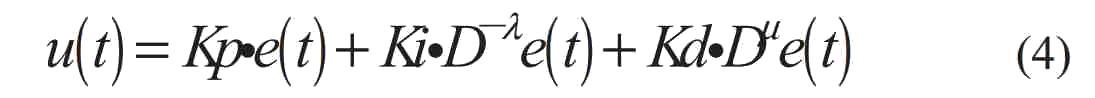
Когда λ и μ принимают разные значения, структура контроллера также будет различной. Оптимизация соответствующих параметров будет корректнее улучшать производительность системы и улучшать эффект управляющего воздействия.
Очевидно, что достаточно сложно производить моделирование MATLAB непосредственно по выражениям (3) и (4). Необходимо сделайте серию приблизительных упрощений. В соответствии с определением дробного исчисления Грюнвальда–Летникова, приближенное выражение уравнения (2) задается его конечным членом [9]. Таким образом, система управления непосредственно исследует временную область или дискретную область для достижения корректных результатов моделирования.
Видно, что он имеет только точность O(h) от уравнения (2), чтобы облегчить последующее описание, выполняется следующая замена:
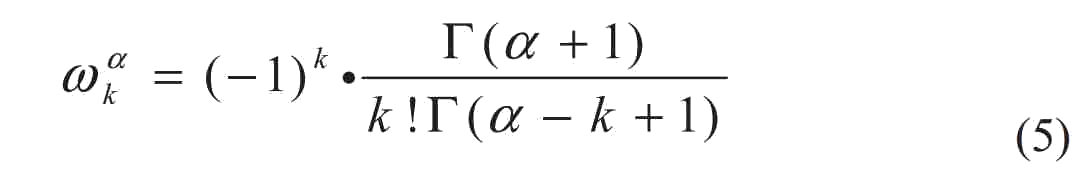
Тогда (2) можно выразить как:
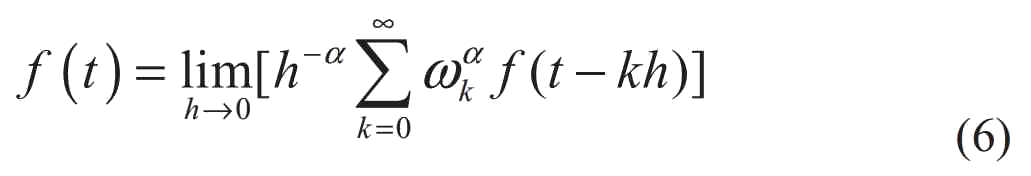
Расширение степенных рядов Тейлора (1-z)α, начиная в начале координат выглядит следующим образом:
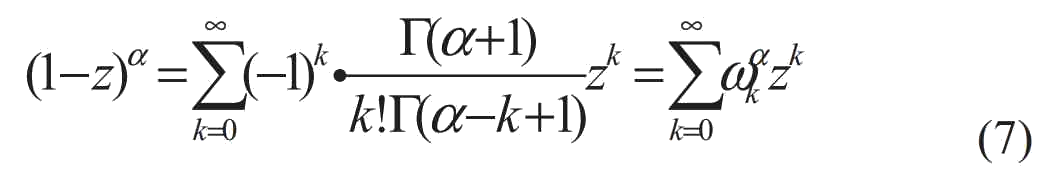
ωkα можно рассматривать как коэффициент разложения степенного ряда Тейлора (1-z)α.
Приближенное выражение дробной производной Грюнвальда–Летникова получается из (6):
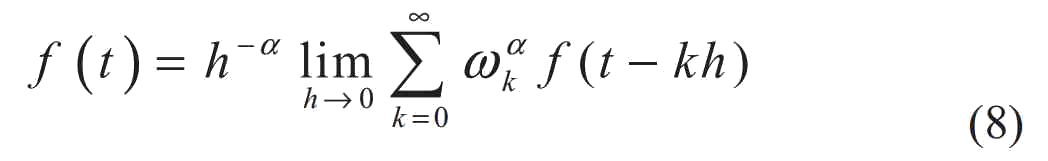
Возьмем T как период дискретизации, Z–преобразование выражения (8) примет вид:
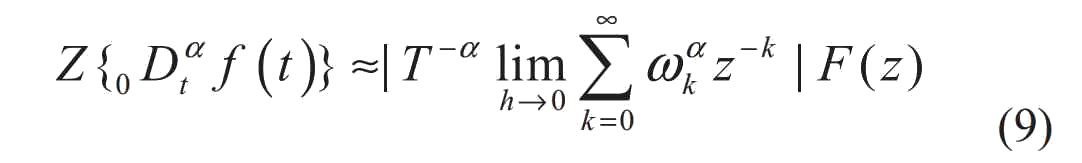
Последнее Z–преобразование выражения (4) [10]:
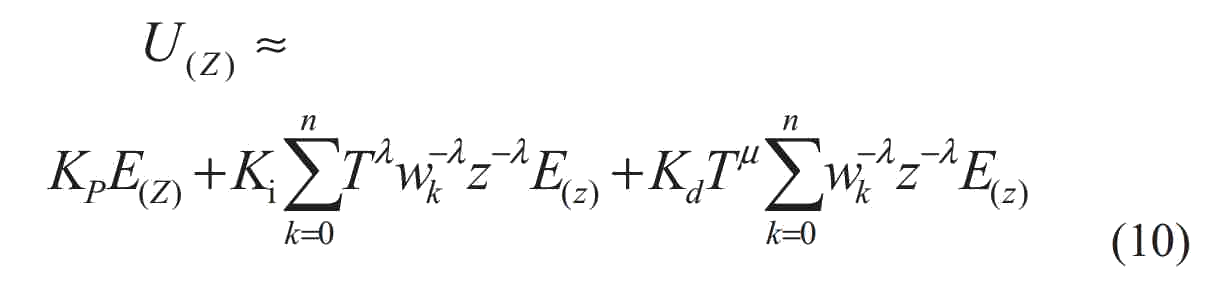
4 Разработка и выбор алгоритма управления
Традиционный ПИД–регулятор может вызвать колебания при изменении объекта. Если параметры ПИД–регулятора не настроены должным образом, произойдет перерегулирование и время регулировки становится больше [11]. Но фракционный ПИД–регулятор имеет лучшую динамическую производительность и более высокую робастность чем традиционный ПИД–регулятор. Согласно соответствующему принципу, система управления с обратной связью дважды замкнутого контура определения скорости и дробной ПИД принимаются в разработку. Он улучшает динамику производительности выходного сигнала, одновременно увеличивая возможности по борьбе с помехами [12]. Блок-схема дробного режима ПИД покаана на рисунке 3.
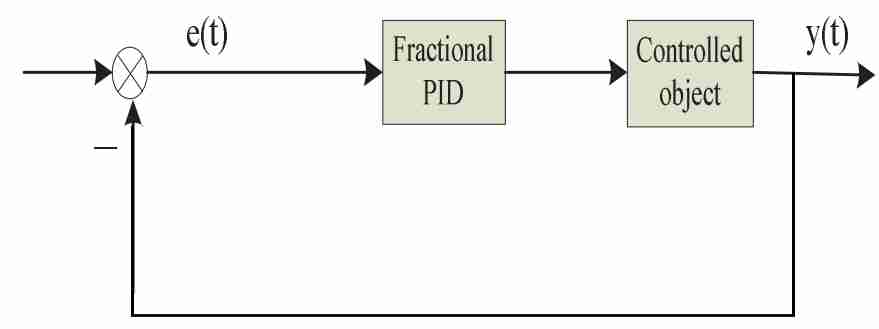
Рисунок 3 – Блок–схема дробного режима ПИД
5 Проектирование и внедрение ПЛИС
Согласно анализу системы бесколлекторного привода, общая структура системы управления на основе ПЛИС состоит из модулей. Весь модуль в основном состоит из модуля генерации ШИМ, ПИД-модуля, AD–мдуля дискретизации, модуля подсчета скорости и модуль коммутации. Конструкция алгоритма системы показана на рисунке 4.
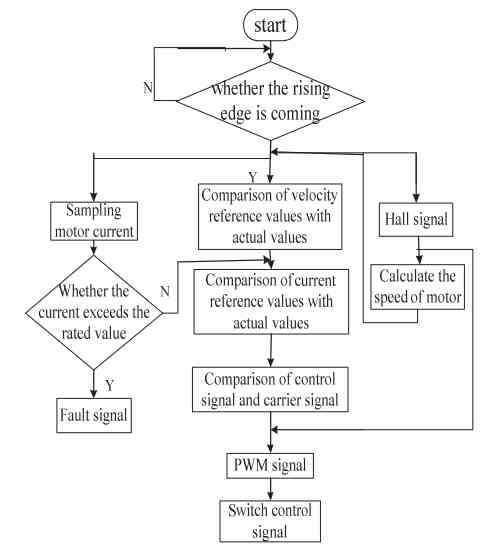
Рисунок 4 – Конструкция алгоритма системы
Сначала инициализируется модуль для запуска программы; а также запускается двигатель в соответствии с сигналом датчика Холла, измерив сигналы тока и положения двигателя; когда вал двигателя вращается, модуль расчета скорости контролирует скорость двигателя в режиме реального времени и отправляет результаты на дважды замкнутый контур управления; Управляющим сигналом является разница скоростей от модуля приемника и модуля обратной связи; ШИМ производит определенную частоту, но неопределенный рабочий цикл для управления двигателем; коммутационный модуль генерирует управляющие сигналы для управления двигателем [2].
6 Анализ моделирования и результатов эксперимента
Общая структура системы разделена на модуль обратной связи и модуль управления приводом. Модуль драйвера генерирует ШИМ–волну. Модуль обратной связи формирует управляющий сигнал. Рисунок 5 показывает форму волны при моделировании модуля двигателя.
Параметры BLDC перечислены следующим образом:
| Мощность | Напряжение | Скорость холостого хода | Номинальная скорость | Номинальный ток | Номинальный момент | Максимальный момент | Ток холостого хода |
|---|---|---|---|---|---|---|---|
Altera's CycloneIIIEP3C40F324I7 использовали в качестве ядра обрабатывающий чип в дизайне. Вершина двигателя BLDC назад EMF сигнал был получен через аппаратную платформу когда рабочий цикл ШИМ составляет 10%. Рисунок 6 – это BLDC обратная электромагнитная волна ротора двигателя.
Как видно из рисунка 7, скорость двигателя BLDC становится стабильным после 0,1 с через дробный порядок ПИД алгоритм. Система имеет очень хорошее управление скоростью двигателя и соответствует требованиям промышленного образца. Результаты моделирования на рисунке 8 подтверждают хороший эффект управления дробного ПИД-регулятора. По сравнению с традиционный регулятор регулятора PI, дробный PID контроллер имеет небольшие колебания, хорошие динамические и статические производительность управления и лучшую надежность.
7 Заключение
Конструкция высокоточного управления двигателем BLDC система на основе FPGA завершена. Дробный порядок PID-алгоритм проверяется платформой FPGA с мощные встроенные возможности. Имитационный анализ алгоритма с помощью аппаратных тестов и MATLAB подтвержден что скорость системы стабильна, а аппаратное обеспечение алгоритм реализации прост. В то же время проверено, что t алгоритм ПИД–дробного порядка улучшает антиинтерференционная способность и стабильность всего система. Система имеет определенное промышленное применение значение.
Список использованной литературы
1. Zhenyong Chu, Weng Muyun, Gao KaijuanFPGA Design and Application. Xi'an University of Electronic Science and Technology Press, Xi'an,2012. 2. Ping Xue, Haichao Wang, Hou Juanjuan, Research on Brushless DC Motor[J]. Control System Based on FPGA.Control Engineering of China. , 2012(S1): 26–30. 3. GUI C.S., CHEN W.M., LIU J.J. et al Designing of DC Motor Control System Based on Nios [J]. Computer Technology and Development, 2011 21(8): 157–159. 4. HUANG Q., HUANGS D, CHEN Z.Y., et al. Variable Structure ADRC Control of Pulse Width Modulation Rectifier under Asymmetrical Input Voltages [J]. Electric machines and control, 18(1): 51–57. 2014. 5. Jihua Wu, Cai Haining, Wang Cheng. Altera FPGA/CPLD Design [M] Beijing:People's Posts and Telecommunications Press, 2011. 6. Hong Zhang, Research and Simulation of fractional order PID controller. Journal of Xi'an University of Posts and Telecommunications, 2011 (01): 107–110. 7. Chunyang Wang, Mingqiu Li, Jiang Shuhua, Wang Yu.Design of fractional order control system Beijing: National Defense Industry Press,2014.8. 8. Zhao C., Zhang X. The application of fractional order PID controller to position servo mechanism. Intelligent Control and Automation, 2008. WCICA 2008. 7th World Congress on.IEEE,2008:3380–3383. 9. Jianlong Gao, Application and Realization of fractional order PID controller in servo system. Nanjing: Nanjing University of Science and Technology, 2013. 10. Zhenbin Wang, Guangyi Cao, Zeng Qingshan, etc., Fractional PID controller and its digital realization. Journal of Shanghai Jiaotong University, 2004, (04): 517–520. 11. Pengliang Chen, Hongjie Hu, Study on fractional-order PID control method based on simulation turntable. Automation Applications. 2017, 1(20). 12. Wei Guo, Li Wang, Zhou Wang-ping, Improvement of Fractional PID Model Predictive Control Algorithm. 2011, 9(5).