Аннотация
Surajit Chattopadhyay, Samarjit Sengupta, Madhuchhanda Mitra Подход по зонам в оценке качества электроэнергии В настоящем документе представлен подход для оценки параметров качества электроэнергии с использованием анализа основных и гармонических сигналов напряжения и тока. Метод трансформации был использован для анализа в трехфазной системе, что в значительной степени уменьшило вычислительные усилия. Вклад фундаментальных и гармонических составляющих в сигналы питания и напряжения силовой системы оценивался отдельно. Был разработан алгоритм для расчета параметров качества электроэнергии из онлайн-сигналов. Этот алгоритм был имитирован для радиальной системы, и результаты сравнивались с результатами, полученными из стандартной системы на основе БПФ. Результаты, как видно, хорошо согласуются с результатами стандартной системы.
Введение
Качество электроэнергии относится к поддержанию близкой синусоидальной формы сигналов напряжений и токов шины распределения питания при номинальной величине и частоте. Причины низкого качества электроэнергии в настоящее время широко определены следующим образом: (i) фактические нагрузки, оборудование, линейные и нелинейные компоненты и (ii) подсистемы систем передачи и распределения, вызывающие импульсы, вырезы, провисание напряжения и затухание, напряжение и текущие дисбалансы, мгновенное прерывание и гармонические искажения. Другими важными факторами низкого качества электроэнергии являются гармоники и реактивная мощность, которые циркулируют контроллерами силовых цепей в энергосистеме.
Исследования продолжаются долго, чтобы изучить влияние дисбаланса и гармоник на качество электроэнергии в энергосистеме [1 – 3]. В несинусоидальной и несбалансированной среде также были предложены некоторые практические определения [4 – 6]. Предложен новый подход к проектированию кривой приемлемости мощности [7]. В таких условиях измерение и мониторинг качества электроэнергии в отношении его дисбаланса и гармоник были представлены в разных публикациях [8 – 13], а также используются различные современные математические инструменты для оценки дисбаланса мощности в системе [8, 15]. Существует несколько существующих методов обнаружения текущих гармоник, таких как быстрое преобразование Фурье (БПФ), теория мгновенной теории, синхронно-эталонная теория, аналоговые или цифровые фильтры и т.д. [16]. В некоторых случаях также используются пассивные фильтры, но они имеют недостатки громоздких компонентов, фиксированные компенсированные характеристики, чувствительность к импедансу линии и последовательный и параллельный резонанс с системой.
В этой статье был предложен подход, основанный на площади, для оценки качества электроэнергии в трехфазной энергосистеме. Неисправности или токи системы без гармоник образуют замкнутый контур вольтамперной или токовой. В этом цикле расщепления появляются с наличием гармоник, порядок которых прямо пропорционален числу расщеплений. Алгоритм был разработан с использованием наземного подхода для расчета активной мощности, реактивной мощности и общих коэффициентов гармонических искажений. Метод трансформации парка использовался для трехфазного измерения коэффициента искажения мощности, что в значительной степени уменьшило вычислительные усилия. Разработанная методика была смоделирована, что хорошо согласуется с результатами стандартных методов.
Оценка преимущественной гармоники
В трехфазной системе напряжение и форма тока могут быть выражены как:

Эти фазные напряжения и линейные токи преобразуются в систему координат с использованием хорошо известной матрицы преобразования Парка [16, 17] следующим образом:
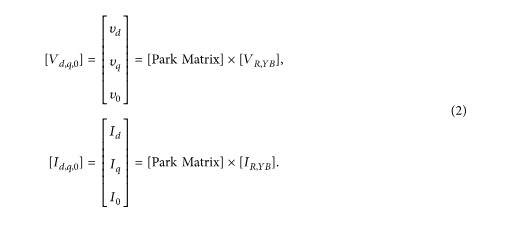
В плоскости, напряжения и токи образуют замкнутые контуры, в которых наличие гармоник приносит расщепления (минимумы), как показано на рисунке 1. Цикл, показанный на этом рисунке, создается волнами, имеющими 5-й порядок гармоник и имеет 4 расщепления. В таблице 1 приведена связь между числом расщеплений и высшим порядком преобладающей гармоники. Число расщеплений (минимумов) увеличивается с увеличением порядка наивысшей гармоники [17]. В заключении, высший порядок nH равен числу расщеплений плюс один, то есть:

Таблица 1: Таблица для числа расщеплений (C) и порядка наивысших гармоник (nH).

Петля образована Id и Iq трехфазной системой, содержащей пятую гармонику.

Рисунок 1 – Петля образована трехфазной системой, содержащей пятую гармонику.
Принцип территориального подхода
Реальные и мнимые части:
Если график напряжения и тока нанесен на плоскость, то площадь, охватываемая одним циклом, определяется как:

Точно так же в плоскости область, покрытая напряжениями и токами в одном цикле, определяется как:

Уравнения (4) и (5) указывают, что содержит информацию о реальной части мощности и содержит информацию о мнимой или реактивной части мощности. Также отмечается, что только гармонические составляющие одного порядка имеют вклады в областях.
Введение опорного сигнала
Если какой-либо один из сигнала напряжения или тока от системы питания доступно, то, что это реальные и мнимые части могут быть разделены путем построения графика сигнала с известным опорным сигналом. Общая форма такого сигнала определяется как:

Здесь есть основная частота опорного сигнала, она должна быть равна основной частоте сигналов напряжения и тока, собранных от энергосистемы, которая изначально является неизвестной величиной. принимается равным 50 Гц, стандартной частоте питания. Затем опорный сигнал отображается с любым из сигналов напряжения и тока. Если петля, сформированная на этом графике, является замкнутой, то основная частота подтверждается как 50 Гц. В противном случае цикл будет разомкнут, то есть между конечной и конечной точкой будет конечный зазор, как показано на рисунке 2. Затем задается как, где - небольшое добавочное значение. должен быть отрегулирован так, чтобы начальная и конечная точка встречались друг с другом. Частота, соответствующая этому контуру, принимается за основную частоту сигнала напряжения и тока, получаемого от энергосистемы. Затем опорный сигнал модифицируется как:

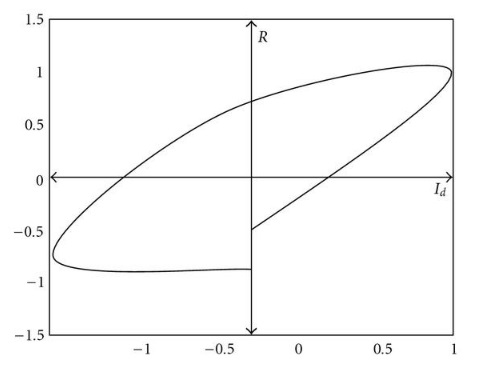
Рисунок 2 – Кривые, образованные R и Id, имеют неравную основную частоту.
Оценка гармонической составляющей
Приведенный выше эталонный сигнал наносится на график соответственно с сигналами напряжения и тока, чтобы найти действительные и мнимые части, как обсуждалось в разделе 3.1. Вклад фундаментальной составляющей оценивается по эталонному сигналу. Для оценки гармоник максимальный предел берется так, как это видно из (4). Вдоль оси амплитуды и фазовые углы для гармонического компонента напряжения и тока определяются как:
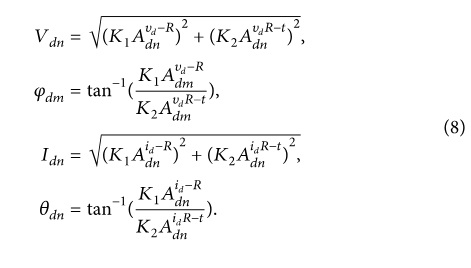
Как и в случае активной и реактивной мощности, компоненты гармоник одного и того же порядка вносят свой вклад, как описано выше, используя (8), реактивная и активная мощность, вносимая гармониками напряжения и тока, записываются как:

Точно так же вдоль оси, амплитуды и фазовые углы для компонента напряжения и тока получены как:

Используя (10), реактивная и активная мощность, вносимые в порядок гармоник напряжения и тока, записываются как:

Коэффициент искажения активной мощности
Коэффициент искажения активной мощности определяется как отношение активной мощности, вносимой гармоническими составляющими, к величине, вносимой фундаментальной составляющей, и определяется как:
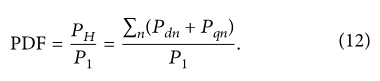
Коэффициент искажения реактивной мощности
Коэффициент искажения реактивной мощности определяется как отношение реактивной мощности, вносимой гармоническими составляющими, к величине, вносимой фундаментальной составляющей, и определяется как:

Суммарная мощность
Общая мощность определяется:
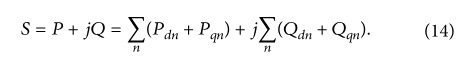
Факторы полного гармонического искажения
Общее гармоническое искажение напряжения по оси определяется как:

Общее гармоническое искажение напряжения по оси определяется как:

Общее гармоническое искажение тока по оси определяется как:
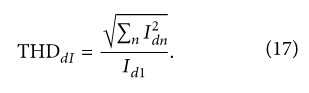
Общее гармоническое искажение тока по оси определяется как:
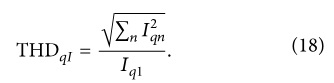
Имитация сети
Трехфазная радиальная система питания, имеющая двигатель и статическую нагрузку, была смоделирована в MATLAB, как показано на рисунке 3. Напряжение на шине 1 и ток, потребляемый от генератора, наблюдаются в шине генератора. Сигнал напряжения понижается с помощью трансформатора напряжения, а сигнал тока понижается с помощью трансформатора тока. Эти сигналы затем дискретизируются с использованием единицы выборки. Выборочные данные оцифровываются и учитываются для формирования петель.
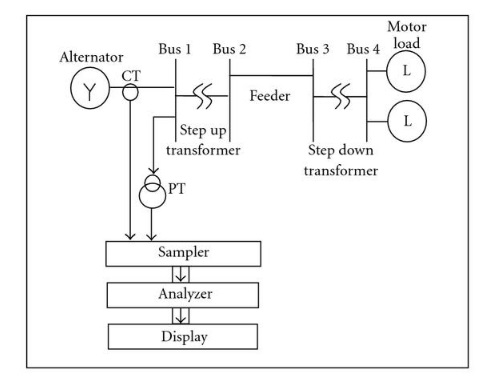
Рисунок 3 – Принципиальная схема моделируемой сети.
Результаты
Различные коэффициенты искажения рассчитываются с использованием вышеуказанного алгоритма. Результат обозначен как расчетное значение. Те же данные оцениваются с использованием анализа Фурье, и результат обозначается как истинное значение. Истинное значение сравнивается с расчетным значением. Ошибка была рассчитана, и были достигнуты удовлетворительные результаты, содержащие низкую ошибку. Результаты выборки при измерении искажения активной мощности, искажения реактивной мощности и общего гармонического искажения представлены в таблицах 2, 3 и 4. Ошибка уменьшается с увеличением частоты дискретизации сэмплера.
Таблица 2:Результаты выборки при измерении искажения активной мощности, искажения реактивной мощности и общего гармонического искажения.
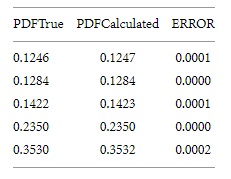
Таблица 3:Результаты выборки при измерении искажения активной мощности, искажения реактивной мощности и общего гармонического искажения.
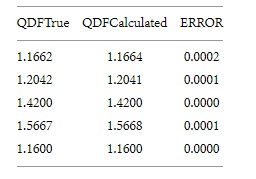
Таблица 4:Результаты выборки при измерении искажения активной мощности, искажения реактивной мощности и общего гармонического искажения.

Выводы
Параметры качества электроэнергии были оценены с использованием анализа основных и гармонических сигналов напряжения и тока. Вместо использования трех линейных токов и трехфазных напряжений, использование d- и q-осных токов и напряжений уменьшает число переменных до четырех (Vd, Vq, Id и Iq) с шести (VR, VY, VB, IR, IY и IB). Следовательно, это уменьшает время выполнения и пространство памяти, необходимое для анализа. Таким образом, техника преобразования Парка в трехфазной системе значительно сократила вычислительные затраты. Тот же самый подход может быть применен для оценки качества каждого отдельного этапа. В таких случаях преобразование Park не потребуется и снова уменьшит вычислительные затраты. Разработан алгоритм для расчета параметров качества мощности по сигналам в режиме онлайн для оценки вклада основных и гармонических компонентов в сигналы напряжения и тока энергосистемы по отдельности. Результаты, полученные на моделируемой сети с использованием алгоритма, были сопоставлены с результатами, полученными с использованием стандартной методики на основе БПФ. Результаты находятся в хорошем согласии с результатами стандартного способа. Небольшая ошибка говорит о приемлемости вышеуказанного подхода на основе области.
Условные обозначения

Список использованной литературы
- A. Domijan, J. T. Heydt, A. P. S. Meliopoulos, M. S. S. Venkata, and S. West,
Directions of research on electric power quality
, IEEE Transaction on Power Delivery, vol. 8, no. 1, pp. 429–436, 1993. - P. P. Barker, J. J. Burke, R. T. Mancao et al.,
Power quality monitoring of a distribution system
, IEEE Transaction on Power Delivery, vol. 9, no. 2, pp. 1136–1142, 1994. - D. D. Sabin, D. L. Brooks, and A. Sundaram,
Indices for assessing harmonics distortion from power quality measurement: definitions and benchmark data
, IEEE Transaction on Power Delivery, vol. 14, no. 2, pp. 489–496, 1999. - S. H. Jaramillo, G. T. Heydt, and E. Neill-Carrillo,
Power quality indices for aperidic voltages and currents
, IEEE Transaction on Power Delivery, vol. 15, no. 2, pp. 784–790, 2000. - A. M. Gaouda, M. M. A. Salama, M. R. Sultan, and A. Y. Chikhani,
Power quality detection and classification using wavelet-multiresolution signal decomposition
, IEEE Transaction on Power Delivery, vol. 14, no. 4, pp. 1469–1476, 1999. - S. Santoso, E. J. Powers, W. M. Grady, and A. C. Parsons,
Power quality disturbance waveform recognition using wavelet-based neural classifier. I. Theoretical foundation
, IEEE Transactions on Power Delivery, vol. 15, no. 1, pp. 222–228, 2000. - S. Santoso, E. J. Powers, W. M. Grady, and A. C. Parsons,
Power quality disturbance waveform recognition using wavelet-based neural classifier. II. Application
, IEEE Transactions on Power Delivery, vol. 15, no. 1, pp. 229–235, 2000. - S. Santoso, W. M. Grady, E. J. Powers, J. Lamoree, and S. C. Bhatt,
Characterization of distribution power quality events with Fourier and wavelet transforms
, IEEE Transactions on Power Delivery, vol. 15, no. 1, pp. 247–254, 2000. - A. Cavallini, G. C. Montanari, and M. Cacciari,
Stochastic evaluation of harmonics at network buses
, IEEE Transactions on Power Delivery, vol. 10, no. 3, pp. 1606–1613, 1995. - S. Leva, A. P. Moronado, and D. Zaninelli,
Evaluation of the line voltage drops in presence of unbalance, harmonics and inter-harmonics: theory and applications
, IEEE Transaction on Power Delivery, vol. 20, no. 1, pp. 390–396, 2005. - M. Karimi-Ghartemani and M. R. Iravani,
Measurement of harmonic/inter-harmonics of time varying frequencies
, IEEE Transaction on Power Delivery, vol. 20, no. 1, pp. 23–31, 2005. - R. Carbone, F. De Rosa, R. Langella, and A. Testa,
A new approach for the computation of harmonics and interharmonics produced by line-commutated AC/DC/AC converters
, IEEE Transactions on Power Delivery, vol. 20, no. 3, pp. 2227–2234, 2005. - A. Ferrero and G. Superti-Furga,
A new approach to the definition of power components in three-phase systems under nonsinusoidal conditions
, IEEE Transactions on Instrumentation and Measurement, vol. 40, no. 3, pp. 568–577, 1991. - H. Akagi and A. Nabae,
The p-q theory in three-phase systems under non-sinusoidal conditions
, European Transactions on Electrical Power Engineering, vol. 3, no. 1, pp. 27–31, 1993. - S. Leva and A. Paolo Morando,
Waves and complex power in transmission lines
, IEEE Transactions on Power Delivery, vol. 18, no. 4, pp. 1320–1327, 2003. - A. Ferrero, A. P. Morando, R. Ottoboni, G. Superti-Furga, and J. L. Willems,
On the meaning of the park power components in three-phase systems under non-sinusoidal conditions
, European Transactions on Electrical Power Engineering, vol. 3, no. 1, pp. 33–43, 1993. - S. Chattopadhyay, M. Mitra, and S. Sengupta,
Power quality analysis in park plane,
in Best of Book Volume on Modeling and Simulation, pp. 8–16, AMSE, Lyon, France, 2006. № 4. С. 72-78.