Аннотация
The mathematical model of unit of an impellent load in a system based on full differential equations of its elements is considered. Expressions for definition of voltage in units of the rated circuit are received. The model allows to expect modes of a group running–down, a self–starting at the breaks of a feed caused by symmetric and asymmetrical short circuits in the circuit of electrosupply with asynchronous and synchronous motors.
Системы электроснабжения с асинхронными и синхронными двигателями получили широкое распространение в различных отраслях промышленности: металлургических и химических предприятиях, магистральных газо- и нефтепроводах, в системах собственных нужд электростанции и др. Типовая схема таких систем электроснабжения приведена на рис. 1. Для анализа их работы при кратковременных нарушениях электроснабжения требуется учет токов подпитки места короткого замыкания от двигательной нагрузки, определение частоты, фазы и уровня напряжения на шинах питания двигателей, учет перетоков мощностей между отдельными двигателями и узлами нагрузки при их групповом выбеге, выбор уставок устройств релейной защиты и автоматики. При этом требуется определение мгновенных значений параметров режимов (токов, напряжений, мощностей, моментов и др.).
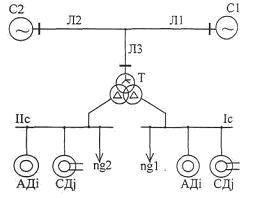
Рисунок 1 – Расчетная схема системы электроснабжения
В работах, посвященных данной теме, в основном рассматриваются узлы нагрузки, содержащие только асинхронные двигатели [1-4], или только синхронные [5–8], и недостаточно освещен вопрос анализа поведения комплексного узла нагрузки, состоящего из произвольного числа асинхронных и синхронных двигателей, статической нагрузки. Кроме того, в указанных работах и других [9-13] рассматриваются и анализируются в основном перерывы питания, вызваны симметричными короткими замыканиями, тогда как известно, что в питающих сетях 110-330 кВ с глухим заземлением нейтрали преобладающими являются однофазные короткие замыкания. Решение указанных вопросов и явилось целью настоящей работы, в которой представлено математическое описание коротких замыканий и режимов группового выбега и самозапуска асинхронных и синхронных двигателей, реализованное в цифровой модели на ПЭВМ. При разработке модели принимались общепринятые допущения для электрических машин и трансформаторов (синусоидальность магнитного потока в зазоре, неучёт насыщения магнитных потоков, симметрия фазных обмоток). Типовая схема системы электроснабжения с асинхронными и синхронными двигателями, аналогичная приведенной в [8], может быть представлена из питающих энергосистем С1 и С2 с соответствующими ЭДС Е1, Е2, линий межсистемных связей Л1, Л2 и линии Л3, подключенной глухой отпайкой к линиям Л1, Л2 для питания через понижающий трансформатор Т двигательной и статической нагрузки на напряжении 6-10 кВ. Трансформатор Т содержит две расщепленные обмотки низшего напряжения и имеет схему соединений Υ/Δ/Δ. В такой схеме будем рассматривать симметричные и несимметричные короткие замыкания и кратковременные перерывы питания на стороне высшего (110-330 кВ) и низшего (6-10 кВ) напряжений.
На рис. 1 изображена одна из типовых схем системы электроснабжения, содержащая АД, статическую нагрузку и шунты на секциях для моделирования различной степени удаленности коротких замыканий на отходящих от шин присоединениях. Трёхфазная схема замещения рассмотренной типовой схемы электроснабжения предоставлена на рис. 2. В этой схеме к каждой из секций 6-10 кВ подключены асинхронные (i = 1,2…n) и синхронные двигатели (j = 1,2…m), статическая нагрузка ng1, ng2, шунты sh1, sh2 для моделирования коротких замыканий, а также обмотки низшего напряжения трансформатора НН1 и НН2. Сеть высшего напряжения представлена обмотками трансформатора, соединенными в звезду, ЭДС систем ЕЛ1 и ЕЛ2, линиями Л1, Л2, шунтом sh3 для моделирования любых видов коротких замыканий, а также заземлениями нейтралей питающих систем, трансформатора Т и шунта sh3.
Способы определения активных сопротивлений и индуктивностей указанных элементов схемы рассмотрены в работах [2, 8, 11, 12]. Асинхронные и синхронные двигатели представлены схемами замещений с двухконтурным эквивалентным ротором по каждой из осей d, q и, кроме того, в синхронных двигателях учтена обмотка возбуждения по оси d. Дифференциальные уравнения статических элементов (трансформатора, питающих линий, шунтов, нагрузки) записываются в фазных координатах а, b, c, o, уравнения асинхронных двигателей – в неподвижных относительно статора координатах a, b, уравнения синхронных двигателей – во вращающихся вместе с ротором каждой машины индивидуальных осях d, q. При этом на каждом шаге расчета, используя соотношения, приведенные в [12], производится преобразование переменных асинхронных и синхронных двигателей к фазным координатам а, b, c. С целью уменьшения количества вычислительных операций в данной модели за основу приняты для асинхронных и синхронных двигателей дифференциальные уравнения, записанные относительно токов статора и ротора [2, 8].
ВЫВОДЫ
1. Разработана математическая модель узла двигательной нагрузки энергосистем, содержащая асинхронные и синхронные двигатели, статическую нагрузку и шунты для моделирования симметричных и несимметричных коротких замыканий. Все элементы узла описаны полными дифференциальными уравнениями и выражены относительно производных токов.
2. Получены аналитические выражения для определения на каждом шаге расчета мгновенных значений напряжения в узлах расчета схемы.
3. Разработанная модель позволяет анализировать режимы группового выбега и самозапуска, коротких замыканий и другие переходные режимы узла комплексной нагрузки, содержащего асинхронные и синхронные двигатели и может быть использована как на стадии проектирования, так и эксплуатации узлов энергосистем.
Список использованной литературы
- Ойрех Я. А., Сивокобыленко В. Ф. Режимы самозапуска асинхронных двигателей. М.: Энергия, 1974. – 96 с.
- Сивокобыленко В. Ф., Лебедев В. К., Кукуй К. А. Математическое моделирование асинхронной нагрузки в режимах группового выбега и самозапуска. – Сб. научн. трудов ДонНТУ. Серия: электротехника и энергетика, вып. 41: – Донецк: ДонНТУ, 2002. – с. 28–34.
- Баков Ю. В. Проектирование электрической части электростанций с применением ЭВМ: Учеб. пособие для вузов. – М.: Энергоатомиздат, 1991. – 272 с.
- Кетнер К. К., Козлова И. А., Сендюрев В. М. Алгоритмизация расчетов переходных процессов автономных электроэнергетических систем. – Рига: Зинатне, 1981. – 166 с.
- Павлюк К., Беднарек С. Пуск и асинхронные режимы синхронных двигателей. Пер. с польск. М., – Энергия, 1971. – 272 с.
- Слодарж М. И. Режимы работы, релейная защита и автоматика синхронных двигателей. – М.: Энергия, 1977. – 216 с.
- Овчаренко А. С., Розинский Д. И. Повышение эффективности электроснабжения промышленных предприятий. – К.: Техника, 1989. – 287 с.
- Сивокобыленко В. Ф., Лебедев В. К., Кукуй К. А. Метод расчета группового выбега синхронной нагрузки электрических систем. – Сб. научн. трудов ДонНТУ. Серия: электротехника и энергетика, вып. 50: – Донецк: ДонНТУ, 2002. – с. 79–87.
- Сыромятников И. А. Режимы работы асинхронных и синхронных двигателей. – М.: Энергоатомиздат, 1984. – 240 с.
- Ковач К. П., Рац И. Переходные процессы в машинах переменного тока. – М. Л., Госэнергоиздат, 1963. – 744 с.
- Сивокобыленко В. Ф., Костенко В. И. Математическое моделирование электродвигателей собственных нужд электрических станций. Донецк, ДПИ, 1979. – 110 с.
- Сивокобыленко В. Ф. Переходные процессы в многомашинных системах электроснабжения электрических станций: Уч. пособие. – Донецк, ДПИ, 1984. – 116 с.
- Голоднов Ю. М. Самозапуск электродвигателей. – М.: Энергоатомиздат, 1985. – 136 с.
- Segeda M. Analysis of power system steady states in phase coordinates on PC. III Sympozjum Metody matematyczne w elektroenergetyce, Zakopane, 1993. – P. 97–99.
- Wamkeue R., Kamwa I., Dai-Do X. Numerical modelling and simulation of unsymmetrical transients on synchronous machines with newtral included // Electric Machines and Power System Journal. – January, 1998.