Моделирование упругих колебаний конструкций крановых установок в пакете Comsol Multiphysics
Автор: Бажутин Д. В.
Источник: Наукові праці ВНТУ, 2013, № 4
Аннотация
Бажутин Д. В. Моделирование упругих колебаний конструкций крановых установок в пакете Comsol Multiphysics. В работе рассмотрены особенности моделирования упругих колебаний механических конструкций в программном пакете Comsol Multiphysics. На примере мостового и башенного кранов показана методика разработки моделей в данном пакете.
Введение
Автоматизация процессов перемещения грузов с помощью крановых установок является в настоящее время актуальной задачей, поскольку позволяет экономить электроэнергию и снизить общее время цикла транспортировки. При этом синтез регуляторов и вывод законов управления зачастую проводят без учета упругих свойств механической части крановых установок. Однако с увеличением длин конструкций их упругие колебания приводят к значительному увеличению механических напряжений, что снижает срок эксплуатации кранов за счет проявления усталости металлов.
Особенностью протяженных конструкций является распределение их массы и жесткости по их длине. В этом случае упругие колебания описывают дифференциальными уравнениями в частных производных, решаемые методом конечных элементов. Поэтому в последнее время для решения таких задач все чаще применяют специализированные программные пакеты, ориентированные на исследование объектов с распределенными параметрами.
Целью данной работы является разработка моделей конструкции башенного и мостового кранов и исследование процесса их перемещения в пакете Comsol Multiphysics
Создание модели
Создание модели в рассматриваемом программном пакете проходит в несколько этапов. Во-первых, необходимо задать размерность графического пространства. С целью упрощения моделей объектов, имеющих оси симметрии в конструкции, предусмотрена возможность создания осесимметричных моделей, которые включают в себя лишь часть всей конструкции. Во-вторых, указывают область исследуемых физических явлений и тип решаемой задачи, например, статический или переходный режим, собственные частоты колебаний и др. После этого необходимо сформировать геометрию исследуемого объекта, для чего имеется довольно удобный графический интерфейс, а также имеется возможность импортирования моделей, созданных в специализированных графических редакторах.
Следующим этапом является указание физических свойств материала, из которого изготовлена конструкция. Перечень необходимых для расчетов параметров зависит от того, к какой области физики относятся исследуемые явления. Например, магнитные поля требуют информации об относительной магнитной проницаемости материала и его электропроводности, а исследование механических колебаний конструкции – о модуле Юнга, коэффициенте Пуассона, плотности выбранного материала и т. п.
Последним этапом создания модели является указание всех внешних воздействий, способов взаимодействия объектов и запретов на перемещения в некоторых направлениях.
Для моделирования процессов в механических системах в пакете Comsol Multiphysics служит модуль Structural Mechanics (структурная механика), содержащий различные библиотеки, предназначенные для моделирования конкретных систем. В частности моделирование упругих колебаний конструкций в пределах зоны текучести материала возможно с помощью библиотек Solid (сплошные тела), Shell (тонкостенные элементы) и Beam (балки). Каждая из этих библиотек имеет ограничения относительно возможности вычисления перемещений и их производных. Так, библиотека сплошных тел позволяет измерять скорости и ускорения по всем трем осям, но не дает информации об углах поворота, библиотека тонкостенных элементов не позволяет измерять линейные скорости и угловые ускорения, а библиотека балок – любые скорости и ускорения. Эти особенности следует учитывать при разработке модели.
В качестве примера рассмотрим процесс создания модели мостового крана (см. рис. 1). За основу примем данные мостового крана 5+5-5К-22,5-10 У2. Исходя из соображений, что в большинстве случаев внешним контуром регулирования в системе автоматизированного кранового электропривода является контур скорости, для создания модели используем библиотеку Solid Mechanics, которая позволяет непосредственно вычислять линейную скорость в любом направлении в любой точке конструкции.

Рисунок 1 – Модель мостового крана.
Точность результатов моделирования, полученных из этой модели, будет зависеть от степени соответствия геометрии модели реальным размерам установки. При этом следует учитывать, что наличие мелких деталей в конструкции значительно увеличивает необходимый для расчетов объем машинной памяти. Поэтому конструкцию целесообразно строить в виде совокупности балок, сечение которых соответствует размерам рассматриваемого крана. В этом случае значительно возрастает масса конструкции, поэтому необходимо снизить плотность и жесткость материала, из которого она выполнена.
Помимо этого, затруднительным является моделирование процесса раскачивания и подъема груза из-за отсутствия возможности создания шарнирных соединений и гибких канатов, а реализация движения тележки по мосту связана с рядом трудностей. Поэтому ограничимся одной грузоподъемной тележкой без груза, жестко зафиксированной в некоторой точке конструкции моста.
Пренебрегая упругостью контакта рельса и колеса, можно считать, что опорные балки крана не могут двигаться в поперечном направлении и по вертикали, что реализуется путем наложения запрета на перемещения нижних граней опорных балок. Усилие, вырабатываемое приводными двигателями, можно реализовать путем приложения эквивалентной по величине силы к крайним граням опорных балок в направлении движения моста. Действие силы тяжести можно учесть, введя распределенную по всему объему конструкции силу, вычисляемую как F = gρ, где ρ – плотность материала.
Установив тележку в средней точке и приложив в течение 1 секунды к крайним граням усилие, получим приведенные на рис. 2 графики составляющих скоростей по двум осям: горизонтальной, вдоль которой осуществляется движение, и вертикальной.
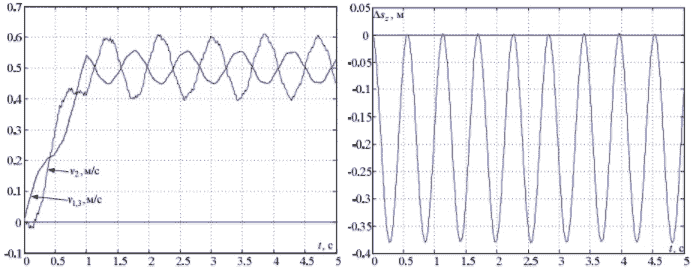
Рисунок 2 – Графики горизонтальных скоростей и вертикальной деформации при центральном расположении тележки
Графики горизонтальных скоростей получены для крайних точек конструкции, а также тележки. Вертикальные перемещения возможны только лишь для главных балок, поэтому величину деформации балок в вертикальном направлении фиксируем в точке, в которой установлена тележка. Очевидно, что в виду симметричности конструкции скорости в крайних точках абсолютно идентичны. Вертикальные колебания имеют незатухающий характер, поскольку силы внутреннего вязкого трения не были учтены при создании модели.
На рис. 3 приведены графики тех же сигналов при учете сил внутреннего трения. В данном случае наблюдается постепенное затухание колебаний, которое тем сильнее, чем выше их частота

Рисунок 3 – Графики горизонтальных скоростей и вертикальной деформации при учете сил внутреннего трения
Таким образом, разработанная модель позволяет проводить исследования упругих колебаний конструкции мостового крана при различных положениях тележки и действии различных сил.
Более сложным представляется процесс создания модели башенного крана, поскольку она имеет решетчатую структуру, состоящую из большого количества балок разного сечения. С одной стороны, все балки можно представить в виде тонкостенных элементов, поскольку толщины применяемых профилей незначительны по сравнению с длиной каждого отдельно взятого элемента. С другой стороны, процесс создания такой модели является крайне сложным, а процесс моделирования – требовательным к вычислительной мощности. Составив конструкцию из сплошных тел, можно было бы добиться достаточной простоты модели при незначительной потери точности результатов. Тем не менее для башенного крана ключевой величиной является угол поворота, возможность прямого измерения которого в этом случае отсутствует. Исходя из этих соображений, модель конструкции башенного крана составим из тонких балочных элементов, каждому из которых поставлено в соответствие некоторое сечение, определяющее его жесткость во всех направлениях. В качестве опорных данных для создания модели была взята информация о кране WOLFF 6071 фирмы Wolffkran AG. Разработанная модель приведена на рис. 4.
При создании этой модели были приняты некоторые допущения. В частности из расчета была исключена тележка с подвешенным к ней грузом. В отличие от мостового крана, грузовая тележка имеет значительно меньшую массу, поэтому несущественно влияет на динамику всей системы. Привод перемещения тележки и подъема груза, а также противовес представляем в виде сосредоточенных масс, расположенных в указанных на рис. 4 точках.
С учетом того, что библиотека балочных элементов не позволяет проводить измерения скорости, а в переходных процессах по перемещению упругие колебания менее выражены, в качестве измеряемого сигнала примем разницу углов поворота между точками, расположенными на оси вращения и на конце стрелы. Полученный график представлен на рис. 5.

Рисунок 4 – Модель башенного крана
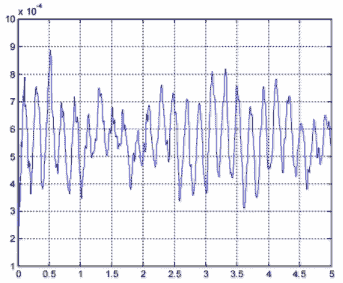
Рисунок 5 – Разница углов поворота
Очевидно, что характер колебаний по сравнению с мостовым краном значительно сложнее. Имеется несколько гармонических составляющих, каждая из которых соответствует определенному режиму собственных упругих колебаний конструкции. Дополнив модель силой тяжести или прикладывая к балкам некоторую нагрузку, имитирующую воздействие ветра, можно получить аналогичные графики, показывающие особенности деформации конструкции в том или ином случае.
Выводы
Пакет Comsol Multiphysics позволяет разрабатывать модели, довольно точно отображающие динамику упругих механических конструкций. По приведенной методике можно разработать модель конструкции произвольной крановой установки и провести исследования ее упругих колебаний.
Список использованной литературы
1. Comsol Multiphysics User’s Guide. Version 4.2, 2011.