Подавление упругих колебаний в трёхмассовых электромеханических системах путем введения корректирующих обратных связей по разностям скоростей движущихся масс
Автор: Божко В.И., Бажутин Д.В.
Источник:Перспективы развития электротехнических, электромеханических и энергосберегающиъ систем
Аннотация
Божко В.И., Бажутин Д.В. Подавление упругих колебаний в трёхмассовых электромеханических системах путем введения корректирующих обратных связей по разностям скоростей движущихся масс. В работе приведён синтез системы подчинённого регулирования скорости электроприводов трёхмассовой электромеханической системы. Для подавления упругих колебаний при синтезе дополнительно учитываются обратные связи по разностям скоростей движущихся масс. С помощью компьютерного моделирования доказана эффективность такого подхода.
Электропривод в современном понятии представляет собой сложную электромеханическую систему, характерной особенностью которой является тесная взаимосвязь процессов в электрической и механической части. Наличие упругих звеньев механической части при взаимосвязи радикально изменяет свойства электропривода в целом и является причиной колебательных явлений в динамике. Колебательные составляющие движения электропривода приводят к отклонению переходных процессов от предписанных технологией и способствуют росту динамических нагрузок на электрическое и механическое оборудование, а также значительно сокращает срок ее службы за счет проявления усталости металла. Таким образом, подавление упругих колебаний является актуальной задачей.
В литературе достаточно много внимания уделено двухмассовым системам [1,2], на динамику которых в значительной степени влияет только одна частота собственных колебаний. Такую модель применяют к системам, в которых две большие масс связаны между собой упругой связью, массой которой пренебрегают.
Гораздо более интересным представляется моделирование про-цесса перемещения системы с относительно равномерно распределённой массой, например, мостового крана с большой длиной пролёта. В этом случае можно принять допущения, что масса главных балок по некоторому закону распределяется между тележкой и концевыми балками, образуя трёхмассовую систему [3-5], структурная схема которой показана на рис.1, где приняты такие обозначения: v1, v2, v3 – скорости точек, в которых расположены сосредоточенные массы m1, m2, m3; F1, F3 – усилия, создаваемые приводными двигателями колес; F12, F32 – упругие силы взаимодействия сосредоточенных масс, c12,c32 – коэффициенты упругости.

Рисунок 1 – Структурная схема трёхмассовой системы
Одним из способов подавления упругих колебаний в двухмассовых электромеханических системах является введение корректирующих обратных связей по разности скоростей движущихся масс. Применим такой же подход для трёхмассовой системы.
В системе есть два электропривода, поэтому необходимо определить два коэффициента обратных связей и две постоянные времени регуляторов скорости. Структурная схема замкнутой системы регулирования приведена на рис.2.
Выполним оптимизацию замкнутых контуров скорости по модульному оптимуму. Для этого запишем передаточную функцию за-мкнутой системы от задания на скорость до скорости второй массы, которая имеет вид:
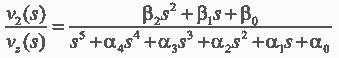
где:
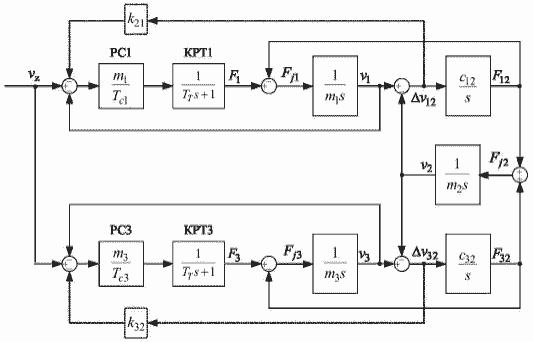
Рисунок 2 – Структурная схема системы подчиненного регулирования скорости трехмассового объекта
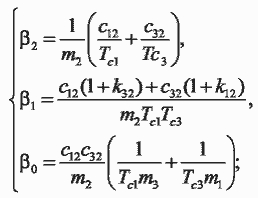
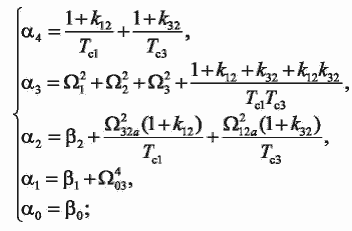
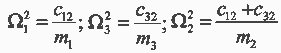
– частоты собственных колебаний движущихся масс;

– частоты собственных упругих колебаний автономных двухмассовых систем с сосредоточенными массами m1-m2 и m3-m2;

– среднегеометрический корень характеристического полинома рассматриваемой трехмассовой системы;
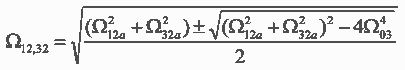
– частоты собственных упругих колебаний трехмассовой системы.
Для выведенной передаточной функции составляем уравнения, обеспечивающее достижение модульного оптимума. Чтобы опреде-лить как неизвестные постоянные времени Tc1,Tc3, так и коэффициенты корректирующих обратных связей k12, k32, необходимо решить систему 4-х уравнений с 4-мя неизвестными:
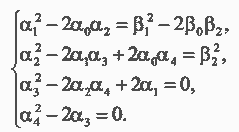
Решение данной системы уравнений выполняем численными методами. В качестве начальных приближений можно использовать значения постоянных времени и коэффициентов обратных связей, полученных при оптимизации автономных двухмассовых систем.
Исследуем процесс подавления упругих колебаний. Для этого примем следующие параметры объекта регулирования m1=m2=m3=20, c12=4000, и c32=2*c12. Результаты моделирования приведены на рис.3а. Параметры системы регулирования дополнительно рассчитаны для таких значений параметров: 1) m1=5кг, m2=m3=20кг, c32=2*c12; 2) m1=60кг, m2=m3=20кг, c32=2*c12. Результаты моделирования приведены на рис. 3б и 3в соответственно.
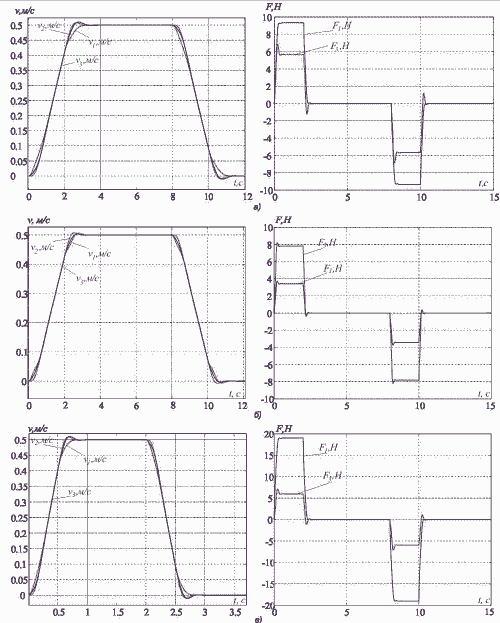
Рисунок 3 - Переходные процессы в системе подчиненного регулирования
Видим, что во всех трёх случаях упругие колебания эффективно подавляются. Качество переходных процессов немного меняется, в сигналах приводных усилий и скоростей присутствует перерегулирование до 5-10%. Таким образом, можно сделать вывод, что предложенная методика позволяет эффективно подавлять упругие колебания в достаточно широком диапазоне соотношения движущихся масс и частот упругих колебаний.
Выводы
Применение корректирующих обратных связей по разностям скоростей движущихся масс позволяет эффективно подавлять упругие колебания в много-массовых системах. В зависимости от соотношения параметров исходной системы качество переходных процессов может немного ухудшаться, возможно увеличение перерегулирования или времени регулирования.
Список использованной литературы
1. Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
2. Коцегуб П.Х., Баринберг В.А., Толочко О.И., Федоряк Р.В. Оптимизация двухмассовых систем регулирования скорости // Известия вузов. Электроме-ханика. – 1998. – №4. – С. 54-57.
3. Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана / О.И. Толочко, Ф. Палис, Д.В. Бажутин // Електромеханічні і енергозберігаючі системи. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія і практика» - Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339.
4. Палис Ф, Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки / Ф. Палис, О.И. Толочко, Д.В. Бажутин // Вісник Національного технічного університету «Харківський політехнічний інститут». – Харків: НТУ «ХПІ», 2013, №36 (1009). – С. 36-39.
5. O. Tolochko, D. Bazhutin. Suppression of horizontal structural vibration of overhead crane in transversal direction given fixed trolley position // Науково-технічний журнал «Електротехнічні та комп’ютерні системи», 2013. - вип. 12(88).