СИСТЕМА УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОМ С ПЛАВНЫМ ИЗМЕНЕНИЕМ ДЕМПФИРОВАНИЯ УПРУГИХ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ

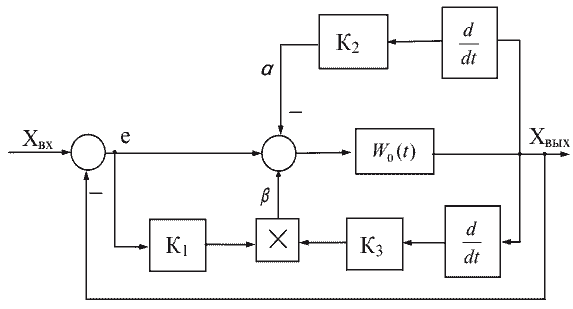
Рисунок 1 – Система с плавным изменением демпфирования по ошибке регулирования.

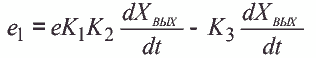
Приведенную на рис. 1 схему системы управления нельзя отнести к универсальной, так как ошибка регулирования е не всегда может быть использована для формирования коэффициента демпфирования. Например, в системе подчиненного регулирования с ПИ-регулятором скорости ошибка регулирования будет близкой к нулю, однако колебания упругого момента будут. Поэтому более целесообразным является использование не ошибки регули рования, а сигнал нарастания (уменьшения) управляющего сигнала.

На рис. 2 приведена типовая система подчиненного управления электроприводом с задающей моделью (ЗМ) и двухмассовой упругой механической системой. Регулятор скорости (PC) и регулятор тока (РТ) приняты пропорционально-интегральными. В качестве электродвигателя (Д) принят двигатель постоянного тока независимого возбуждения с тиристорным преобразователем мощности (ТП). J₁J₂ – соответственно моменты инерции ведомой и ведущей масс; C_У – коэффициент упругости, С_Дф – коэффициент демпфирования колебаний.

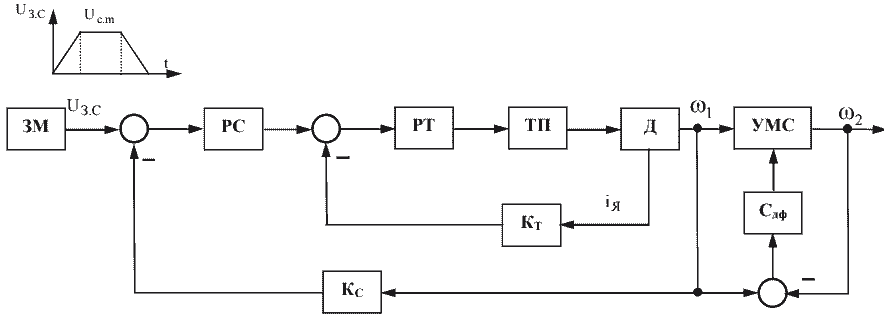
Рисунок 2 – Simulink-модель системы управления с плавным демпфированием упругих колебаний.

Известно, что при определенном значении С_Дф колебаний в системе не будет. Однако в электромеханических системах с упругими звеньями типа стальных канатов, упруго-вязких конвейерных лент реализовать нельзя, так как нельзя осуществлять подачу сигнала, пропорционального С_Дф.

Управляющим воздействием на систему принят сигнал U_З.С , пропорциональный заданной диаграмме скорости.

Современые технические средства позволяют контролировать скорости и перемещения сосредоточенных масс. Поэтому целесообразно сигнал, пропорциональный разности скоростей ведущей (ω₁), и ведомой (ω₂) масс, подавать на один из входов системы управления, например, на вход регулятора тока

В принятой системе подчиненного регулирования передаточные функции регуляторов тока и скорости равны:

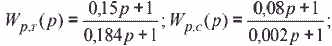
передаточная функция тиристорного преобразователя

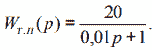
Передаточная функция замкнутого контура тока

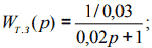
Коэффициент пропорциональности тока (ЭДС) C_д = 2,63; моменты инерции масс: J₁ = 23; J₁ = 4;6 параметры упругого звена: C_У = 60; С_{Дф = 100.}

Задающая модель (ЗМ) формирует два управляющих воздействия, пропорциональных заданным диаграммам скорости и положения (в случае позиционного электропривода) при ограничениях максимальной скорости, ускорения и положения. Основным входным воздействием является разность сигналов

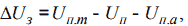
где U_Пm- сигнал заданного положения; U_П – текущее (контролируемое) перемещение; U_Па – расстояние до конечного положения рабочего органа с момента начала замедления.

Таким образом, замедление начинается с момен та равенства нулю ΔU_З причем положение и скорость контролируются на всем периоде замедления благодаря уменьшению до нуля сигнала U_П.a.

Плавное увеличение коэффициента демпфирования осуществляется пропорционально изменению сигнала заданной скорости в период разгона и замедления.

Функциональная схема устройства формирования коэффициента демпфирования (УФКД) представлена на рис. 3. На вход функционального преобразователя (ФП) подается сигнал заданной скоро сти U_СЗ , а управляющий сигнал ΔU_З , определяющей начало замедления системы определяется автоматически в ФП. Выходной сигнал ФП, изменяю - щийся от 0 до 1 перемножается с максимальным значением коэффициента демпфирования C_дф.m (штриховой линией показана диаграмма ОАВС сигнала заданной скорости). В точке В сигнал демпфирования снижается до нуля и начинает увеличиваться до максимального значения согласно диаграмме скорости и к концу рабочего цикла K_Дф достигает максимального значения С_Дф.

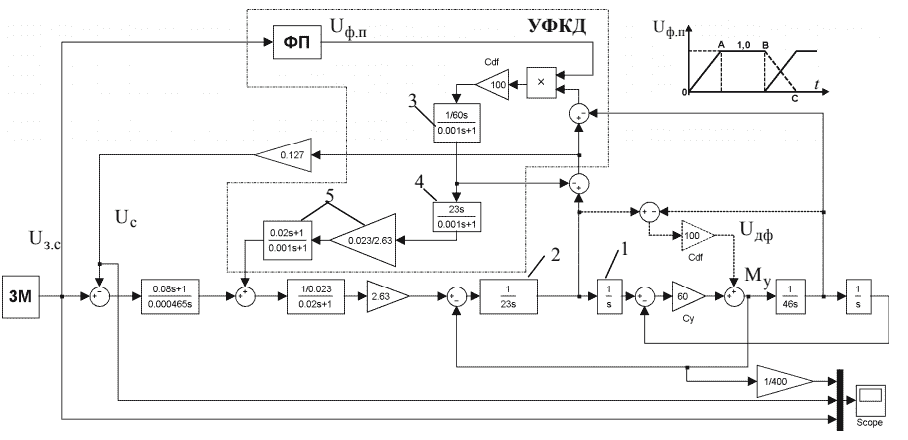
Рисунок 3 – Simulink-модель системы управления с плавным демпфированием упругих колебаний.

Для реализации такого режима с использованием системы управления согласно правилам преобразования структурных схем сигнал U_Дф=(ω₁-ω₂)С_Дф - переносится на вход регулятора тока (исходная схема включения демпфирующего элемента показана на рис. 3 штриховыми линиями). Перенос воздействия U_Дф через интегрирующие звенья 1 и 2 реализован соответственно блоками 3 и 4, а через передаточную функцию замкнутого контура тока и коэффициент 2,63 с помощью блока 5. При этом идеальное дифференцирование реальными дифференцирующими звеньями с малыми постоянными времени, равным 0,001с.

Блоки 3, 4, 5 совместно с нелинейными функциональными элементами составляют УФКД упругих колебаний в переходных режимах. Это устройство, реализуемое на цифровом микроконтроллере, обеспечивает плавное изменение упругого момента от 0 до максимального значения в переходных режимах.

На рис. 4 показаны графики изменения сигналов скорости (U_з.с, U_с) и упругого момента М_у при плавном изменении демпфирования (а) и при отсутствии демпфирования (б). В первом случае график действительной скорости практически совпадает с заданной при отсутствии колебаний упругого момента. Во втором случае наблюдаются существенные упругие колебания, причем наибольшая их амплитуда достигается после останова двигателя. Это свидетельствует о том, что после остановки двигателя ведомая масса упругой системы (как правило, это рабочий орган) будет совершать колебательные процессы. Поэтому, например, в шахтных клетевых подъемных установках используются специальные посадочные устройства, удерживающие массу в неподвижном состоянии.

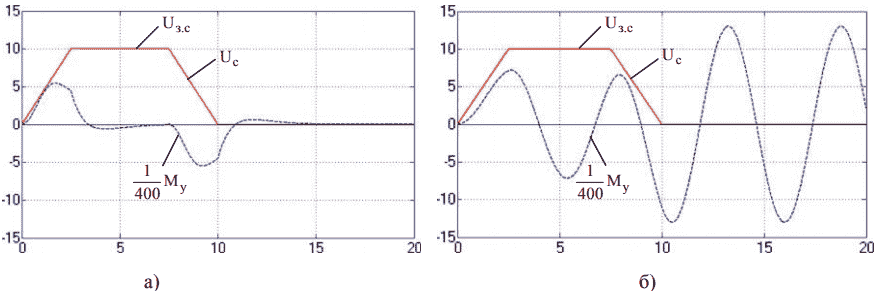
Рисунок 4 – Графики изменения сигналов скорости и упругого момента в переходных режимах: а) при плавном изменении демпфирования; б) при отсутсвии демпфирования.

Одним из современных требований к электроприводам шахтных подъемных установок, лифтам высотных зданий является остановка концевого груза (клети или кабины) на заданном уровне без применения механического тормоза с последующим его наложением на неподвижную систему.

Для реализации таких режимов предлагаемый способ демпфирования упругих колебаний имеет особое значение. Подход к решению данной задачи основан на использовании функциональных законов управления. Управляющий сигнал является нелинейной функцией от входного воздействия при гибких обратных связях по упругому моменту, которыми являются скорости перемещения сосредоточенных масс.

Выводы

1. Для электромеханических систем, в которых рабочий орган соединен с электродвигателем с помощью упругого звена малой жесткости, важным является гашение упругих колебаний в переходных режимах (особенно в период замедления до полной остановки), используя систему управления.

2. Устранение колебательных процессов наиболее эффективно достигается на основе нелинейных законов управления по управляющему воздействию и реальной скорости механизма. Установлена возможность использования в качестве входного воздействия ошибки регулирования или непосредственно входного сигнала в период пуска и замедления.

3. Плавное демпфирование с использованием входного сигнала является универсальным способом и может распространяться на любые системы электропривода. Передача входного сигнала, эквивалентного желаемому коэффициенту демпфирования, может быть реализована с помощью микроконтроллера различными способами в зависимости от типа привода

Литература

1. Чермалых В.М., Родькин Д.И., Каневский В.В. Системы электропривода и автоматики рудничных стационарных машин и установок. – М.: Недра, 1976. – 400 с.
2. Чермалых А.В., Данилин А.В., Майданский И.Я. Моделирование систем оптимального по динамическим нагрузкам управления электроприводом // Електромеханічні і енергозберігаючі системи. – Кременчук, 2007. – С. 61-65.
3. Чермалых В.М., Алтухов Е.И., Данилин А.В., Козаченко А.В. Моделирование сложных электромеханических систем с переменной частотой упругих колебаний // Вісник КППУ. – Кременчук. 2008. – Вип. 3/2008 (50). - С. 168 – 171.
4. Хлыпало Е.И. Нелинейные системы автоматического регулирования. М.: Энергия, 1967. – 450 с.
5. Дьяконов В. Simulink 4. Специальный справочник. – СПб.: Питер, 2002. – 528 с