Исследование системы управления мостовым краном с устранением колебаний

Ключевые слова

Система управления устраняющая колебания; груз ; колебания; мостовой кран; принцип максимума Понтрягина .

I. ВВЕДЕНИЕ

Мостовые краны широко используются в промышленных условиях для транспортировки грузов из одного места в другое. Из-за высоких требований к безопасности и к углу колебаний, высокой точности позиционирования и малого времени транспортировки, управление краном - сложная работа, которая должна быть автоматизирована. Однако на практике в промышленности большинство машин управляются вручную хорошо обученными операторами. Эта ситуация приводит к низкой производительности труда и низкой безопасности работы.[1]. Поэтому, некоторые исследователи начали заниматься проблемой управления мостовыми кранами [2]. Было предложено новое fuzzy управление для устранения колебаний и управления положением мостового крана на основе модели нечетких логических выводов с единым правилом (SIRMs). Скорость и положение тележки, а так же угловая скорость и угол отклонения каната были выбраны в качестве входных данных, а ускорение тележка в качестве выходных. Если начальные условия не обнуляются или возникают неисправности при перемещении, то следует использовать систему уравнения с замкнутым контуром. В случаях, когда необходимо управлять поворотным механизмом крана могут использоваться системы, управляющие угловой скоростью стрелы. Угловое ускорение стрелы крана рассматривается как выход этих систем. [6].

Для тележек был предложен нелинейный регулятор с использованием метода Ляпунова [7]. Затем был использован модифицированный вариант управления скользящей поверхности для управления положением тележки. [7]. Для подвесного мостового крана был разработана система управление с нечеткой логикой с идеей управления скольжением[8]. Авторы в [9] предложили нелинейный закон управления для стабилизации мостового крана с тремя степенями свободы, используя теорему Ласалля. В [10] нелинейная следящая система для управления скоростью и положением груза был разработан с двумя контурами: внешний контур был предназначен для слежения за положением, а внутренний контур для стабилизации колебаний с использованием расчета единой искаженной конструкции . Однако желаемый результат был получен только для случая, когда движущая сила искажающих колебаний намного быстрее, чем движущая сила тележки. В [11] была предложена нелинейная схема управления, включающая механизм адаптации параметров, для обеспечения общей стабильности замкнутой системы. При использовании разработанного регулятора ошибка по положению сводится к нулю, а искажающие колебания быстро демпфируются до достижения стабилизации.

Известно, что определенные типы грузоподъемных механизмов приводят к двойной маятниковой движущей силе [12]. Много исследователей работало над решением проблемы, связанной с движущей силой двойного маятника [13]. Их работы можно условно разделить на две категории: управление с обратной связью и формирование входных данных. Метод управления с обратной связью использует измерения и оценку состояния системы для подавления колебаний [12, 14, 15]. В [13] была представлена командно-сглаживающая схема для подавления сложных колебаний груза. Для анализа динамического режима кранов и надежности этого метода было использовано моделирование большого диапазона движений. Для того чтобы удовлетворить спрос на более быструю обработку грузов, движение крана должно управляться таким образом, чтобы его динамические характеристики были оптимизированы. В частности, управление мостовыми крановыми системами направлено на выполнение, как контролирования положения, так и устранения колебаний[16]. Поскольку колебания груза зависят от ускорения тележки, уменьшение рабочего времени и уменьшение колебаний груза частично противоречит требованиям. Задача управления с устранением колебаний заключается в том, чтобы уменьшить колебания груза при максимально быстром перемещении его в желаемое положение [17]. Одним конкретным и эффективным подходом с прямой связью для снижения колебаний в машинах является формирование входных данных [18]. Для управления механическими системами в [19] был предложен новый метод быстрого управления. Контроллер включает в себя пропорционально-дифференциальный регулятор (PD). Для мостового крана эта система управления может реализовывать как отслеживание положения, так и устранения колебаний [19]. В [20] был предложен эволюционный алгоритм для основанной на данных нечеткой логики прогнозируемой модели времени между отказами и разработки адаптивной системы управления краном.

В данной статье обсуждаются возможности оптимизации управления мостовым краном для повышения точности позиционирования груза и сокращения времени транспортировки.

II. МОДЕЛЬ И МОДЕЛИРОВАНИЕ

Разработана имитационная модель мостового крана с использованием программного обеспечения MATLAB / Simulink [21]. Предыдущее исследовательские работы [22] показали, что во время транспортировка мостовым краном происходит значительное колебание груза. Колебания отрицательно влияют на производительность оборудования, и обычно требуется уменьшить амплитуду колебания груза до допустимого уровня. Чтобы уменьшить амплитуду колебания груза, можно применять следующие меры:

– Оборудование, которое прикладывает усилие к грузу в определенные моменты времени. Направление такой силы противоположно направлению отклонения груза.

– Стабилизирующая сила также может быть приложена к точке крепления груза посредством

Интересно сравнить оба подхода управления.

Динамическая модель мостового крана представлена на рисунке 1. Кран состоит из трех частей: грузоподъемного механизма, тележки и моста.

Положение массы M_? (рисунок 1) можно описать следующими формулами:

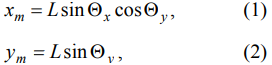
где L - длина каната:

где L0 - длина каната без прикрепленного груза, которая определяется угловым положением барабана для каната, ?L - удлинение каната, вызванное нагрузкой. Угол отклонения каната (рисунок 1) составляет:

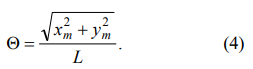
Вертикальное смещение груза (рисунок 1), вызванное колебанием:

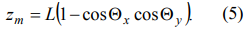
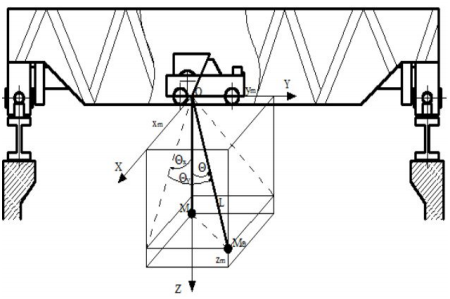
Рисунок 1 – Динамическая модель мостового крана.

Уравнения (1-5) используются для определения кинетической и потенциальной энергии механической системы грузоподъемного механизма, а также ее диссипативной функции в уравнениях Лагранжа второго рода. При создании математической модели был оценен опыт промышленного предприятия Vilniaus kranai AB, в котором утверждалось, что угловое отклонение каната от вертикали не превышает 5 градусов. Полученные после соответствующей обработки в соответствии с методиками, представленными в [23], уравнения и используемые координаты представлены в [21]. Моделирование механической системы проводилось со следующими параметрами (данные получены из экспериментов, проведенных в Vilniaus kranai AB): стандартная масса g = 9,81 м / с2, масса груза M = 1000 кг, масса тележки Mx = 5000 кг, масса тележки и моста My = 10000 кг, коэффициент демпфирования в точке крепления каната H2 = 1 Нм / рад, коэффициент демпфирования каната H1 = 1000 Нс / м, начальная жесткость канатного натяжения C1 = 1716000 Н / м, коэффициент демпфирования тележки по оси X Hx = 1000 нс / м, демпфирование крана по оси Y Hy = 2000 нс / м.

Нелинейность зависимости удлинения каната от нагрузки учитывается в математической модели. Для простоты описания были введены две дополнительные координаты и их производные:

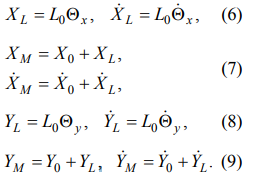
Полученная модель описывает механическую систему мостового крана и изменения положения груза, вызванные изменениями положения точки крепления каната в направлениях X и Y и наклоном груза на канате под углами ?x и ?y (рисунок 1). Силы Fx и Fy создаются двигателями тележки и моста и определяют точку крепления движения каната. Двигатели управляются контроллерами. Алгоритм управления может быть основан на принципе максимума Понтрягина [24]. Если тележка движется с низким рассеянием энергии и при отсутствии возмущающей силы (которая не может превышать значение, заранее определенное мощностью двигателя), оптимальная фазовая траектория состоит из двух парабол. На первом участке (ускорение) управляющий параметр u=1 и траектория описываются следующим уравнением:

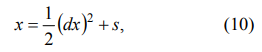
где s - произвольная постоянная. На втором участке (замедление) управляющий параметр u= – 1 (т.е. двигатель перевернут), и фазовая точка перемещается к параболе, которая пересекает нулевую точку координат:

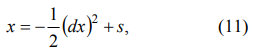
Оптимальная траектория при отсутствии возмущающей силы и условий рассеяния энергии представлена на рисунке 2.

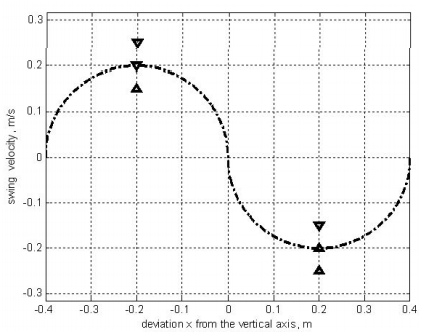
Рисунок 2 – Оптимальная фазовая траектория в соответствии с принцип максимума Понтрягина.

Для изучения динамического поведения механической системы крана была разработана диаграмма Simulink. Подсистема управления описана в [21]. Модель работает следующим образом. Тяговое усилие прикладывается от двигателя моста (вход Fx) к модели и движению тележки вдоль оси X к точке начала координат. В периоды ускорения и торможения фазовые траектории описываются в (10) и (11) для случая незначительных диссипативных сил. Если рассеяние энергии является значительным, кривые ускорения и замедления отличаются от парабол. При создании модели Simulink предполагалось, что в случае отключения питания двигателя соответствующие колеса тормозятся, а затем освобождаются при включении двигателя.

На рис. 3 (а) показана зависимость силы тяги Fx от времени для случая простого торможения приводом. График зависимости амплитуды колебаний нагрузки от времени, полученный при вертикальном подъеме груза, представлен на рисунке 3 (б). Тяговое усилие считалось измененным в тот момент, когда точка намотки каната на барабан расположена над местом назначения груза. Фазовая траектория груза представлена на рисунке 3 (с). Увеличение амплитуды колебаний наблюдается во время торможения привода (рис. 3 (б)). В случае применения предлагаемой системы устранения колебаний, фазовая траектория нагрузки должна совпадать с оптимальной траекторией в соответствии с принципом максимума Понтрягина (рис. 2).

Установлено, что уменьшение силы тяги с 1300 до 1200 Н исключает увеличение амплитуды колебаний груза, возникающее из-за изменения силы тяги (рис. 4 (а), 4 (б)). Однако колебания, возбуждаемые движением груза, сохраняются в течение значительного времени (рис. 4 (с)). Более детальное изучение динамики нагрузки показало влияние фазы колебаний в момент изменения силы тяги. Можно констатировать, что в случае небольшого отклонения каната от вертикального положения плавный переход к оптимальной фазовой траектории осуществляется со значительным уменьшением тягового усилия при сохранении направления его приложения (рисунок 5). Эффективное демпфирование колебаний может быть достигнуто также путем изменения силы тяги (Рисунки 6 (a), 6 (b)). В этом случае величина силы, которую необходимо приложить в противоположном направлении, составляет только часть первоначального значения (рис. 6 (а)). Также достигается плавный переход к оптимальной фазовой траектории (рис. 6 (с)). В случае значительного отклонения каната от вертикального положения в момент изменения тягового усилия (рисунок 7) своевременный переход фазовой траектории на оптимальную траекторию обеспечивается увеличением тягового усилия при сохранении направления его приложения. Степень изменения величины и направления тягового усилия зависит от угла отклонения каната от вертикали. В случае небольшого отклонения каната от вертикального положения в момент изменения тягового усилия, колебания нагрузки уменьшаются путем уменьшения тягового усилия при сохранении направления его приложения.

III. ВЫВОДЫ

Исследования показали, что применение принципа максимума Понтрягина позволяет разработать систему управления приводом мостового крана, способную обеспечить эффективное демпфирование колебаний каната. В целях упрощения системы управления, величина и направление тягового усилия должны быть изменены в тот момент, когда точка намотки каната на барабан расположена над местом назначения груза. Однако, если необходимо уменьшить время демпфирования до минимума, направление тягового усилия следует изменить, в то же время его величину следует уменьшить. Если в момент изменения тягового усилия отклонение троса близко к амплитуде колебаний, эффективное демпфирование колебаний обеспечивается увеличением тягового усилия при сохранении направления его приложения. Предлагаемая система управления способна управлять как тележными, так и мостовыми приводами.

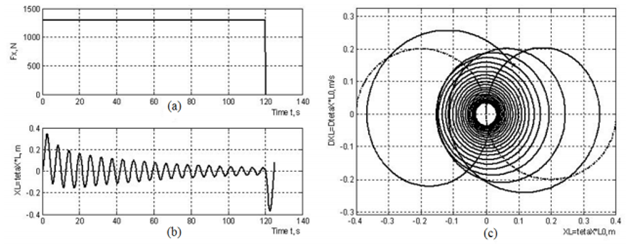
Рисунок 3 – Сила тяги (a) и амплитуда колебаний груза (b) в зависимости от времени и графика фазовой траектории (c), полученные в случае отсутствия системы устранения колебаний.

Рисунок 4 – Тяговое усилие (а) и амплитуда колебаний груза (b) в зависимости от графика времени и графика фазовой траектории (в), полученные для случая уменьшения тягового усилия с 1300 до 1200 Н.

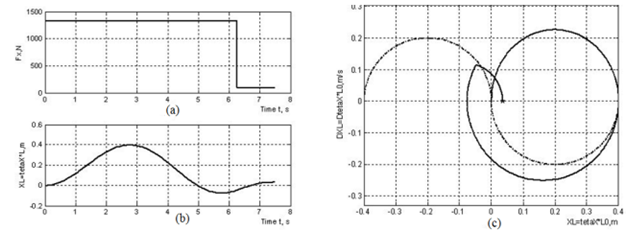
Рисунок 5 – Сила тяги (a) и амплитуда колебаний груза (b) в зависимости от графика времени и графика фазовой траектории (c), полученные для случая небольшого отклонения каната от вертикального положения в момент изменения силы тяги.

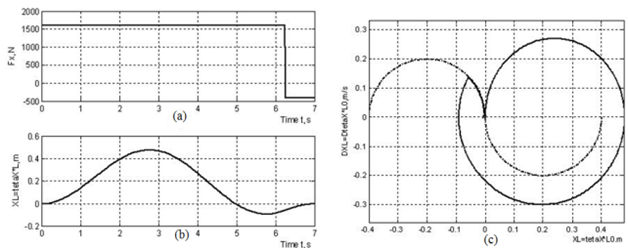
Рисунок 6 – Сила тяги (a) и амплитуда колебаний груза (b) в зависимости от времени и графика фазовой траектории (c), полученные для случая изменения силы тяги.

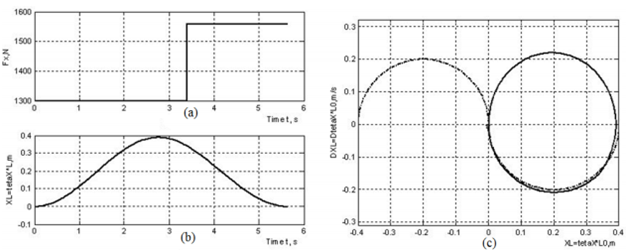
Рисунок 7 – Сила тяги (a) и амплитуда колебаний груза (b) от графика времени и графика фазовой траектории (c), полученные для случая значительного отклонения каната от вертикального положения в момент изменения силы тяги.

Перечень ссылок

1. N. Sun, Y. Fang, “New energy analytical results for the regulation of underactuated overhead cranes: an end-effector motion-based approach”, IEEE Transactions on Industrial Electronics, Vol. 59, No. 12, pp. 4723- 4734, 2012
   
2. K. C. C. Peng, W. Singhose, D. H. Frakes, “Hand motion crane control using radio-frequency real-time location systems”, IEEE/ASME Transactions on Mechatronics, Vol. 17, No. 3, pp. 464-471, 2012
   
3. K. C. C. Peng, W. Singhose, D. H. Frakes, “Hand motion crane control using radio-frequency real-time location systems”, IEEE/ASME Transactions on Mechatronics, Vol. 17, No. 3, pp. 464-471, 2012
   
4. M. Fliess, J. Levine, P. Rouchon, “A simplified approach of crane control via a generalized state-space model”, 30th IEEE Conference on Decision and Control, pp. 736-741, 1991
   
5. A. J. Ridout, “Anti-swing control of the overhead crane using linear feedback”, Australian Journal of Electrical and Electronics Engineering, Vol. 9, No. 1-2, pp. 17-26, 1989
   
6. G. G. Parker, B. Petterson, C. Dohrmann, R. D. Robinett, “Command shaping for residual vibration free crane maneuvers”, 1995 American Control Conference, pp. 934-938, 1995
   
7. ] B. Vikramaditya, R. Rajamani, “Nonlinear control of a trolley crane system”, 2000 American Control Conference, pp. 1032-1036, 2000 [8] D. T. Liu, J. Q. Yi, D. B. Zhao, “Fuzzy tuning sliding mode control of transporting for an overhead crane”, 2003 International Conference on Machine Learning and Cybernetics, pp. 2541-2546, 2003
   
8. ] Y. Fang, W. E. Dixon, D. M. Dawson, E. Zergeroglu, “Nonlinear coupling control laws for a 3-DOF overhead crane system”, 40th IEEE Conference on Decision and Control, pp. 3766-3771, 2001
   
9. J. Yu, F. L. Lewis, T. Huang, “Nonlinear feedback control of a gantry crane”, 1995 American Control Conference, pp. 4310-4315, 1995
   
10. J. H. Yang, K. S. Yang, “Adaptive coupling control for overhead crane systems”, Mechatronics, Vol. 17, No. 2-3, pp. 143-152, 2007
    
11. ] Y. Al-Sweiti, D. Soffker, “Modeling and control of an elastic shipmounted crane using variable gain model-based controller”, Journal of Vibration and Control, Vol. 13, No. 5, pp. 657-685, 2007
    
12. J. Huang J, Z. Liang, Q. Zang, “Dynamics and swing control of doublependulum bridge cranes with distributed-mass beams”, Mechanical Systems and Signal Processing, Vol. 54-55, pp. 357-366, 2015
    
13. S. Lahres, H. Aschemann, O. Sawodny, E. P. Hofer, “Crane automation by decoupling control of a double pendulum using two translational actuators”, 2000 American Control Conference, pp. 1052-1056, 2000
    
14. Z. N. Masoud, A. H. Nayfeh, N. A. Nayfeh, “Sway reduction on quayside container cranes using delayed feedback controller: simulations and experiments”, Journal of Vibration and Control, Vol. 11, No. 8, pp. 1103-1122, 2005
    
15. A. H. W. Chun, R. Y. M. Wong, “Improving quality of crane-lorry assignments with constraint programming”, IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), Vol. 37, No. 2, pp. 268-277, 2007