Аннотация
Горячев В.Я., Елинов Д.А., Кудашев А.В. Важной характеристикой систем электроснабжения является способность обеспечивать бесперебойное и качественное питание потребителей. Основным показателем качества является способность энергетической системы сохранять или восстанавливать свои свойства после различных нарушениях нормального режима работы, вызванного слабыми или сильными воздействиями на систему. Слабые воздействия на систему в основном обусловлены перегрузкой электроэнергетических систем. Токи элементов энергетических систем при таких воздействиях лишь в незначительной степени превышают номинальные значения. Устойчивость системы к слабым воздействиям оценивается коэффициентами статической устойчивости энергетической системы.
Важной характеристикой систем электроснабжения является способность обеспечивать бесперебойное и качественное питание потребителей. Основным показателем качества является способность энергетической системы сохранять или восстанавливать свои свойства после различных нарушениях нормального режима работы, вызванного слабыми или сильными воздействиями на систему. Слабые воздействия на систему в основном обусловлены перегрузкой электроэнергетических систем. Токи элементов энергетических систем при таких воздействиях лишь в незначительной степени превышают номинальные значения. Устойчивость системы к слабым воздействиям оценивается коэффициентами статической устойчивости энергетической системы. Именно статическая устойчивость определяет возможность энергетической системы к сохранению работоспособности в условиях выхода из строя отдельных узлов электроэнергетической системы.
Нарушение нормального режима работы системы энергоснабжения может быть вызвано сильными воздействиями на систему. К сильным воздействиям на системы электроснабжения относят воздействия, связанные, как правило, с резким увеличением токов системы до значений, превышающих номинальные токи в десятки раз. Такие воздействия могут привести к нарушению динамической устойчивости, что сопровождается изменением частоты сети, резким колебаниям напряжения и переходу части генераторов системы в асинхронный режим работы.
При проектировании новых энергетических систем и при модернизации старых возникает острая необходимость в прогнозировании характеристик энергетических систем. Одним из путей определения устойчивости систем является теоретический анализ режимов работы при сильных и слабых воздействиях на систему. Учесть реальные параметры каждого элемента системы практически невозможно из–за их огромного количества и сложности взаимодействий этих параметров даже внутри каждого элемента. Необходимость решения проблемы приводит к значительной идеализации параметров элементов. Однако и идеализация параметров не всегда приводит к положительному результату из-за сложности самих систем электроснабжения.
Трудности, связанные с громоздкостью и сложностью теоретического анализа устойчивости электроэнергетических систем, вызывают желание разработчика переложить решение задач устойчивости на плечи компьютеров. В таком случае можно идти путем составления программ в одной из сред программирования или путем моделирования переходных процессов в одной из специально разработанных сред. Широкие возможности для моделирования энергосистем и процессов, происходящих в них, предоставляет пакет программ MatLab.
При анализе работы электрических систем необходимо учитывать не только электромагнитные параметры системы, но и связанные с ними механические параметры элементов системы, если эти параметры влияют на электромагнитные процессы в системе. Речь идет прежде всего о первичных двигателях (турбинах), генераторах электрической энергии, автоматических регуляторах, двигателях нагрузки, где электрическая энергия, получаемая из распределительной сети системы, преобразуется в механическую. Следует отметить то, что под динамимической устойчивостью понимают способность системы восстанавливать после больших возмущений исходное состояние или практически близкое к исходному (допустимому по условиям эксплуатации системы). Под статической устойчивостью электрической системы понимается ее способность восстанавливать исходный режим после кратковременного воздействия малого возмущения. В качестве параметров обычно принимают напряжение в узловых точках и токи в ветвях ЭС, а под возмущением понимают изменение механического момента на валу двигателя одного из генераторов или мощности нагрузки. Вследствие малости рассматриваемых возмущений, энергетическая система при анализе статической устойчивости может рассматриваться как линейная динамическая система. Нарушение статической устойчивости может происходить вследствие причин различной физической природы. Если мощность турбины, например, достигнет максимально возможного значения электромагнитной мощности генератора, происходит апериодическое нарушение устойчивости. При работе генератора в режиме холостого хода или при малой мощности, передаваемой через линию электропередач (ЛЭП), обладающую значительным активным сопротивлением, возможно самораскачивание турбогенератора. Аналогичное явление происходит в виде нарастающих колебаний угла при неправильной настройке автоматического регулятора возбуждения (АРВ). Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата. При оперативном управлении системой расчеты предельных режимов должны проводиться с учетом изменения схемно–режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.
Принципы анализа статической и динамической устойчивости продемонстрированы на примере электро- энергетической системы, состоящей из электростанции, представленной эквивалентным генератором G , повышающего трансформатора T1, двухцепной линии L1, L2 , повышающего трансформатора T2 и сети бесконечной мощности NET . Такая схема подключения станции к энергетической системе является традиционной. Имитационная модель системы представлена на рисунке 1. По условным обозначениям, используемым в модели, не трудно определить местоположение перечисленных элементов системы. На модели представлены и контрольно–измерительные приборы, используемые для контроля электрических и механических параметров электроэнергетической системы. Для измерения электрических и механических величин генератора используется специальный измерительный блок, предназначенный для контроля параметров электрических машин MMD. На его вход подается информация с выхода m генератора. Между генератором и трансформатором T1 включен комплект измерительных приборов, предназначенных для контроля режимов работы трехфазных цепей KIP1. На выходе второго трансформатора включен аналогичный измерительный блок.
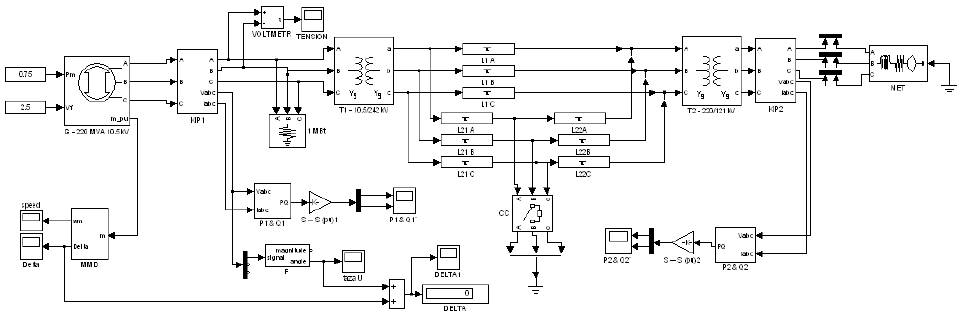
Рисунок 1 – Имитационная модель электрической станции, работающей на электроэнергетическую систему большой мощности
Имитация трехфазного короткого замыкания в системе реализуется с помощью короткозамыкателя CC. Момент срабатывания короткозамыкателя и длительность нарушения режима устанавливается в окне параметров блока.
Модель имитирует работу генератора без АРВ. На вход блока подается значение мощности генератора в относительных единицах Pm и напряжение возбуждения Vf . Изменение напряжения возбуждения позволяет регулировать электродвижущую силу синхронной машины работающей в генераторном режиме.
Исследование статической устойчивости системы передачи электрической энергии производится следующим способом. Путем изменения численного значения мощности турбины на входе m P генераторного блока изменяют мощность электрической энергии, отдаваемой генератором в сеть. При этом изменяется фазовый сдвиг электродвижущей силы холостого хода генератора и напряжения сети. В синхронном генераторе изменяется взаимное положение ротора генератора и магнитного поля статора. Если электромагнитный момент сопротивления ротора генератора равен механическому моменту вращения турбины, то сохраняется устойчивое равновесие системы. Однако при определенной величине электродвижущей силы генератора, напряжении сети и характеристиках системы передачи электрической энергии существует максимальное значение мощности, которую может передать рассматриваемая система. Если мощность турбины превышает предельное значение, механический момент турбины не уравновешивается электромагнитным моментом генератора. Это приводит к нарушению статической устойчивости системы. Нарушение статической устойчивости приводит к тому, что частота вращения ротора становится больше номинальной скорости, частота электродвижущей силы генератора становится больше частоты сети. Все это приводит к резким скокам тока системы. Элементы защиты должны отключить генератор от системы. В противном случае это может привести к нарушению устойчивости всей электроэнергетической системы.
Статическая устойчивость системы оценивается коэффициентом, численное значение которого определяется отношением разности предельной мощности и реальной мощности генератора к реальной мощности генератора в рассматриваемый момент времени. Коэффициент статической устойчивости рассматриваемой системы при номинальной мощности генератора равен 0.55.
Нарушение устойчивости системы может быть вызвано сильными воздействиями на элементы системы передачи электрической энергии. Достаточно часто причиной нарушения нормального режима работы системы является короткое замыкание на линии электропередачи, вызванное нарушением изоляции после разряда молнии. Для имитации короткого замыкания в модели используется короткозамыкатель CC . Предполагается, что короткое замыкание происходит в середине второй цепи линии электропередач. Момент пробоя изоляции и длительность воздействия устанавливается в окне задания параметров короткозамыкателя.
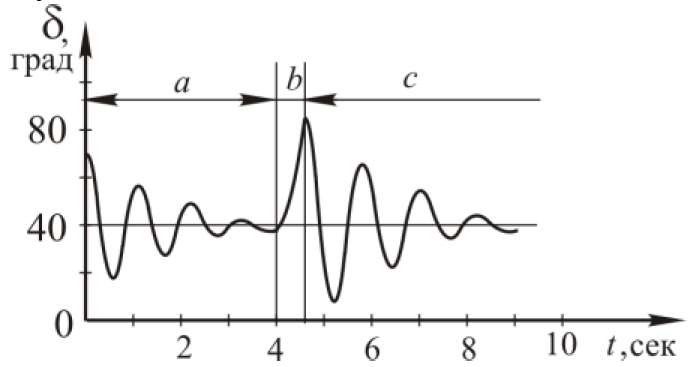
Рисунок 2 – Изменение угла δ при длительности короткого замыкания равной 0.6 сек
О нарушении устойчивости системы можно судить по изменению частоты вращения генератора, изменению тока линии или изменению угла фазового сдвига между напряжением сети и электродвижущей силой генера- тора δ(t). На рисунке 2 приведен график зависимости фазового сдвига от времени. На графике четко выделяются три отрезка времени, соответствующие трем режимам работы системы. В течение отрезка вре- мени a , равном 0.4 секунды, осуществляется пуск всей системы передачи электроэнергии. Переходный процесс пуска системы заканчивается примерно через 4 секунды. При этом ротор генератора совершает колебания около устойчивого значения угла, равного 40 градусам.
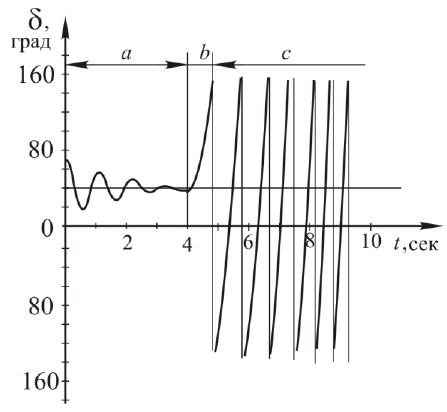
Рисунок 3 – Изменение угла δ при длительности короткого замыкания, равной 0.8 сек
В момент времени t=4 секунды наступает короткое замыкание во второй цепи линии электропередачи. Количество энергии, отдаваемое электростанцией в сеть, резко сокращается и механический момент тур- бины не уравновешивается электромагнитным моментом генератора. Угол δ резко возрастает. Это подтверждается графиком изменения угла во времени на отрезке b , представленным на рисунке 2. График соответствует длительности короткого замыкания, равной 0.6 секунды. Максимальное значение угла составляет примерно 90 градусов. В момент времени t=4.6 секунды повреждение ликвидируется. Система возвращается в устойчивое состояние в течение отрезка времени c.
После сильного воздействия ротор совершает колебания относительно угла устойчивого равновесия δ=40 градусам. Таким образом, при длительности короткого замыкания, равной 0.6 секунды устойчивость системы сохраняется, система еще способна восстановить работоспособность после короткого замыкания.
Устойчивость нарушается при длительности короткого замыкания, равной 0.8 секунды. На рисунке 3 представлен график изменения угла δ при длительности короткого замыкания, равной 0.8 секунды. Обозначения отрезков времени аналогичны обозначениям предыдущего графика. Короткое замыкание в системе наступает в момент времени, равный 4 секундам. В течение отрезка времени, равного длительности короткого замыкания, ротор генератора под действием избыточного механического момента проворачивается на угол, превышающий критическое значение, при котором возврат в устойчивый режим работы уже не возможен. Нарушается синхронный режим работы генератора, что представлено на графике в форме восходящих линий в течение отрезков времени, соответствующих увеличению частоты вращения ротора на один оборот. На графике отрезок времени, соответствующий асинхронному режиму работы системы, обозначен отрезком c .
Исследование режимов работы энергосистем путем моделирования в среде MatLAB в значительной степени сокращает затраты на проектирование энергосистем. При этом такой метод анализа обладает наглядностью и позволяет прогнозировать поведение системы при работах, связанных с модернизацией электроэнергетических систем. Правда для анализа сложных систем электроснабжения необходимо иметь компьютеры с достаточно высоким быстродействием и большим объемом памяти.
Список использованной литературы
1. Горев А.А. Переходные процессы синхронной машины. – М.;Л.: Госэнергоиздат, 1950.
2. Сыромятников И.А. Режимы работы синхронных генераторов. – М.;Л.: Госэнергоиздат, 1952.
3. Конкордиа Ч. Синхронные машины. Переходные и установившиеся процессы. – М.;Л.: Госэнергоиздат, 1959.
4. Эксплуатация турбогенераторов с непосредственным охлаждением / Под ред. Л.Г. Мамиконянца. – М.: Энергия, 1972.
5. Мамиконянц Л.Г. Анализ некоторых аспектов переходных и асинхронных режимов синхронных и асинхронных машин. – М.: ЭЛЕКС–КМ, 2006.
6. Коган Ф.Л., Мамиконянц Л.Г. Асинхронный режим мощных турбогенераторов. – Электричество, 1977, №4.
7. Коган Ф.Л. Анормальные режимы мощных турбогенераторов. – М.: Энергоатомиздат, 1988.
8. Коган Ф.Л. Осуществимость асинхронного режима мощного турбогенератора и оценка возможности предотвращения отключения энергоблоков. – Электрические станции, 1983, №4.
9. Коган Ф.Л. Влияние гасительного сопротивления на асинхронный режим высокоиспользованного турбогенератора. – Электричество, 1974, № 10.
10. Беркович М.А., Семенов В.А. Основы автоматики энергосистем. – М.: Энергия, 1968.
11. Авторские свидетельства (СССР): №553708, БИ, 1977, №13; №649093, БИ, 1979, №7; №767889 БИ, 1980, №36; №858166 БИ, 1981, №31.
12. Коган Ф.Л., Баракин К.А., Воронин Г.И., Фридман М.М.
Защита турбогенераторов от потери возбуждения и асинхронного режима. – В сб. Энергетика и электрификация
. – М.:
Информэнерго, 1979, вып.1.
13. Бронштейн Э.Л., Травина Ю.Я., Шейнкман А.Г. и др.
Сравнительные испытания датчиков асинхронного режима турбогенераторов при потере возбуждения. – Электрические станции, 1979, №6.