Аннотация
Гук О.М. ,Одинцов А.В., Севастьянова А.В., Смоловик С.В. В настоящее время анализ статической апериодической устойчивости энергосистемы проводится в программах расчетов установившихся режимов путем утяжеления исходного сбалансированного установившегося режима до нарушения сходимости итерационного процесса расчета. Для определения значения перетока активной мощности в контролируемом сечении, соответствующего нормативному запасу устойчивости, процесс утяжеления проводится многократно с использованием различных траекторий утяжеления. В настоящей работе исследуется характер изменения якобиана уравнений установившегося режима (УУР) электроэнергетической системы при утяжелении режима по различным траекториям и оценивается возможность использования числового значения определителя матрицы Якоби УУР энергосистемы для оценки положения энергосистемы относительно границы статической устойчивости.
В настоящее время распространенной практикой является анализ показателей статической устойчивости электроэнергетических систем (ЭЭС) на основе использования программ расчета установившихся режимов. Возможность такого решения основывается на том, что при малых возмущениях нелинейные уравнения, описывающие переходные процессы ЭЭС, могут быть линеаризованы, и определитель линеаризованной системы при определенных условиях совпадает с определителем матрицы Якоби уравнений установившегося режима (УУР). Исследование статической апериодической устойчивости требует расчета установившегося режима ЭЭС и определения знака свободного члена характеристического уравнения. Совпадение свободного члена характеристического уравнения системы с якобианом системы УУР дает возможность судить о нарушении статической апериодической устойчивости энергосистемы по нарушению сходимости решения уравнений установившегося режима (что соответствует переходу якобиана через нуль).
В работе [1]. показано, что свободный член характеристического уравнения ЭЭС практически совпадает с якобианом системы УУР ЭЭС только при выполнении следующих условий:
- балансирующий узел в системе совпадает с базисным;
- для генераторных узлов в качестве независимых переменных задаются активные мощности генераторов и модули напряжения на их шинах;
- в нагрузочных узлах при расчетах режимов задаются те же статические характеристики, что и при расчетах статической устойчивости. Следует отметить, что в основе допущения о совпадении якобиана УУР и свободного члена характеристического уравнения лежит допущение о бесконечных значениях коэффициентов усиления АРВ по напряжению.
Согласно методическим указаниям [2], в установившемся режиме работы энергосистемы должен быть обеспечен запас устойчивости по активной мощности. Значение нормативного коэффициента запаса принимается 20% для нормальных режимов, 8% для послеаварийных.
В настоящее время для определения наличия в энергосистеме нормативного коэффициента запаса статической апериодической устойчивости используется метод утяжеления (последовательное изменение параметров исходного устойчивого режима с приближением к границе области устойчивости). В практических расчетах оценка запаса по статической устойчивости требует неоднократного утяжеления исследуемого режима работы энергосистемы. Первоначально посредством утяжеления исходного режима по заданной траектории находится предельный по статической устойчивости режим, затем утяжелением по той же траектории находится режим, соответствующий нормативному коэффициенту запаса.
Целью настоящего исследования является выявление возможности использования определителя матрицы Якоби для оценки устойчивости системы без многократного последовательного утяжеления режима.
Рассмотрим изменение определителя матрицы Якоби при утяжелении режима в электрической схеме, состоящей из генератора (СМ), линии электропередачи (ЛЭП) напряжением 500 кВ и шин бесконечной мощности (ШБМ). На рис. 1 показана изменение значения определителя матрицы Якоби при утяжелении режима в рассматриваемой схеме.
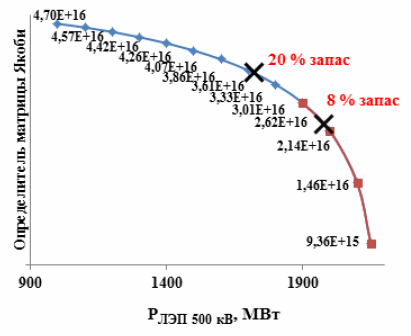
Рисунок 1 – Изменение якобиана при приближении к пределу статической устойчивости
Как следует из рис. 1, изменение определителя матрицы Якоби при утяжелении
режима носит нелинейный характер. Условно характеристику изменения определителя
матрицы Якоби можно разделить на две зоны. Зона 1 – характеристика практически
линейная. Малое изменение мощности на каждом шаге процесса утяжеления
соответствует малому изменению якобиана. В зоне 2 происходит изменение характера
зависимости: на каждом последующем шаге малое увеличение мощности соответствует
все большему уменьшению якобиана (на рисунке данный участок выделен крупными
точками). Система, работающая в зоне 2, находится в устойчивом состоянии, однако
здесь малое изменение параметров режима по траектории утяжеления может привести к резкому уменьшению якобиана, приближая его к нулю и, следовательно, к границе
области статической апериодической устойчивости. В связи с этим назовем условно
зону 2 Зона неустойчивости
, зону 1, соответственно, условно обозначим как Зона
устойчивости
. Следует отметить, что последняя точка на графике соответствует
окончанию процесса утяжеления, в этой точке находится последний установившийся
режим работы при движении
системы по заданной траектории утяжеления, на
следующем шаге якобиан меняет свой знак и система становится статически
неустойчивой.
На рис. 1 обозначены значения активной мощности, соответствующие 20%
запасу и 8% запасу по статической апериодической устойчивости. Рассмотрим случай,
когда исследуемая система находится в послеаварийном режиме работы. Например,
исходно система состояла из СМ, двух ЛЭП и ШБМ. Произошло аварийное
отключение ЛЭП. Согласно [2] допустимым режимом работы является передача по
ЛЭП мощности, отвечающей нормативному коэффициенту запаса 8%. Из данных,
приведенных на рис. 1, следует, что значение мощности, отвечающее коэффициенту
запаса 8%, находится в Зоне неустойчивости
. В таком состоянии системы малое
изменение параметров режима может привести к значительному уменьшению
определителя матрицы Якоби, что означает резкое приближение к границе статической
апериодической устойчивости. Таким образом, для рассматриваемой системы может
быть рекомендовано большее значение коэффициента запаса по статической
апериодической устойчивости.
Рассмотрим изменение определителя матрицы Якоби в модели энергосистемы, состоящей из 1223 узлов и 1562 ветвей. В рассматриваемой энергосистеме имеется 142 генераторных узла, при этом в качестве независимых переменных выбраны активные мощности генераторов и модули напряжения на их шинах. Электрическая сеть состоит из узлов и ветвей с номинальным напряжением 750, 330, 220, 110, 35, 10 и 6 кВ. На рис. 2 показано изменение определителя матрицы Якоби при утяжелении режима по трем траекториям. По оси абсцисс приведены значения мощности, передаваемой по ЛЭП, которой соответствует максимальный угол передачи. По оси ординат приведены значения определителя матрицы Якоби, уменьшенной в 2500 раз.
Траектория 1 была составлена таким образом, чтобы в предельном режиме наибольшее значение угла передачи соответствовало одной из ВЛ 750 кВ.
Траектория 2 была составлена таким образом, чтобы при нарушении статической устойчивости в предельном режиме наибольшее значение угла передачи соответствовало одной из ВЛ 330 кВ. Для оценки применимости рассматриваемого метола в ремонтных схемах в базовом режиме одна ЛЭП 330 кВ принята выведенной в ремонт.
Траектория 3 была составлена таким образом, чтобы в процессе утяжеления режима максимальный угол передачи соответствовал ВЛ 220 кВ. В базовом режиме принималось, что две ЛЭП 220 кВ выведены в ремонт.
Для каждого базового режима отдельно выбирался базисный узел. В качестве базисного узла принималась электрически удаленная от района исследования крупная электростанция.
Из данных, приведенных на рис. 2, следует, что изменение якобиана при
утяжелении режима имеет схожий характер для различных траекторий утяжеления. Как
и для случая схемы генератор – линия – шины бесконечной мощности
, на графиках
изменения якобиана можно выделить две зоны: 1 Зона – равномерное уменьшение
определителя матрицы Якоби при увеличении передаваемой мощности, 2 Зона – резкое
уменьшение якобиана при прежнем шаге утяжеления.
На рис. 2 показаны значения активной мощности, отвечающие нормативным
коэффициентам запаса по устойчивости. В рассмотренных примерах указанные
значения мощности попали в Зону устойчивости
.
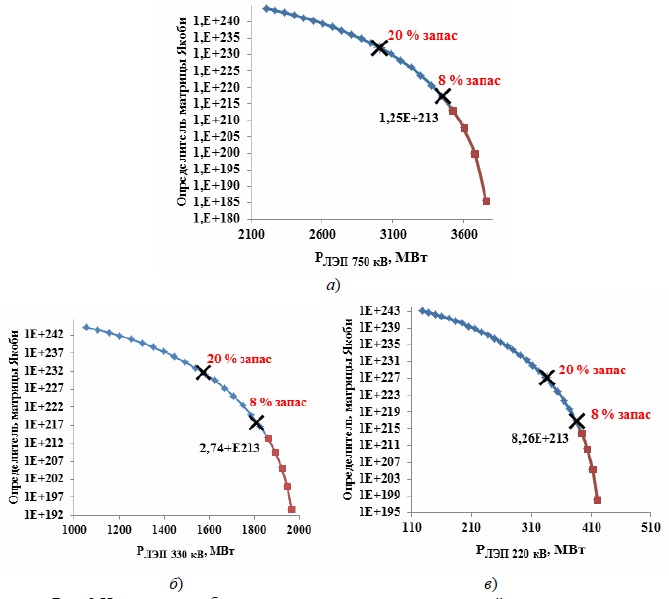
Рисунок 2 – Изменение якобиана в процессе утяжеления в крупной энергосистеме а) утяжеление по 1 Траектории; б) утяжеление по 2 Траектории; в) утяжеление по 3 Траектории
Для уточнения точки характеристики, в которой происходит резкое уменьшение
значений якобиана при прежнем изменении мощности (точка начала Зоны
неустойчивости
), были рассчитаны относительные отклонения каждой точки от
линейной характеристики. Уравнение прямой было составлено по первым двум точкам
графика. Расчеты показали, что резкое отклонение графика уменьшения якобиана в
процессе утяжеления режима от линейной характеристики для всех трех
рассматриваемых случаев происходит в точке, где определитель якобиана имеет
степень 213. Эта точка показана на каждом из графиков рис. 2.
Из вышесказанного следует, что значение определителя матрицы Якоби, которое
соответствует переходу системы в Зону неустойчивости
, является свойством
рассматриваемой энергосистемы и не зависит от траектории утяжеления.
Данное наблюдение дает возможность предположить, что числовое значение
определителя матрицы Якоби может быть использовано для оценки статической
устойчивости. В практических расчетах необходимо один раз провести процесс
утяжеления в модели рассматриваемой энергосистемы, построив график изменения
якобиана, и определить числовое значение определителя матрицы Якоби, соответствующее началу Зоны неустойчивости
. После этого можно рассчитывать
значение определителя матрицы Якоби в любом интересующем устойчивом режиме
работы энергосистемы и делать выводы о положении системы относительно границы
статической апериодической устойчивости.
Summary
Nowadays, the analysis of small-signal (aperiodic) stability of power systems is carried out in computer programs intended for steady state calculations by step-by-step loading of the initial balanced mode until the convergence of steady state calculation process is disturbed. In order to define the active power flow over the controlled group of transmission lines satisfying the normative requirements, the process of step–by–step loading is performed repeatedly using a number of different loading trajectories.
In the presented article, the behavior of the Jacobi matrix determinant of power system steady state equations during the process of step–by–step loading is investigated, and the possibility of using the value of Jacobi matrix determinant for small–signal stability margin assessment is estimated.
Keywords: electric power system, small–signal stability, steady state, step–by–step loading trajectory, Jacobi matrix.
Список использованной литературы
1. Тарасов В.И. Теоретические основы анализа установившихся режимов
электроэнергетических систем. Новосибирск: Наука, 2002, 344 с.
2. Методические указания по устойчивости энергосистем. Москва: Изд– НЦ ЭЭНАС, 2004.