Анотация
А. П. Ковалев, И. И. Москвина, А. А. Павлович. Используя способ разложения сложных по структуре схем замещения систем по базовому элементу и теорему о сумме вероятностей несовместных событий, разработан метод оценки надежности структурно-сложных невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях. Для сложных по структуре невосстанавливаемых систем, у которых вероятность отказов элементов (отказ типа «короткое замыкание») будет меньше либо равна 0,1,то для приведения схемы замещения системы к смешанной структуре предложен способ преобразования логического «треугольника» в эквивалентную по надежности «звезду» и логическую «звезду» в эквивалентный по надежности «треугольник». Приведен пример расчета надежности сложной по структуре системы.
Ключевые слова:
Сложная по структуре система, надежность, схема замещения, базовый элемент, отказ типа обрыв цепи
, отказ типа короткое замыкание
, треугольник-звезда
, звезда-треугольник
.
Понятие, определение, актуальность
Под системой в данном случае будем понимать совокупность взаимосвязанных, конструктивно независимых изделий, которые обладают свойством перестраивать свою структуру в результате случайного повреждения некоторых ее элементов, без нарушения (частичного нарушения) выполнения поставленной перед ней задачи.
Под элементом системы следует понимать – объект, представляющий собой простейшую часть системы, отдельные части которого не представляют самостоятельного интереса в рамках конкретного рассмотрения [1].
Под объектом следует понимать техническое изделие определенного целевого назначения, которое рассматривается в период проектирования, производства, испытаний и эксплуатации [2].
К невосстанавливаемым будем относить такие восстанавливаемые системы, восстановление которых по каким-либо причинам невозможно в рассматриваемый период времени [2].
Под вероятностью безотказной работы невосстанавливаемой системы, элементы которой могут находиться в трех несовместных состояниях, будем понимать меру ее надежности, которая характеризуется вероятностью того, что в течение заданного интервала времени не произойдут такие случайные события, в результате которых разрывается связь или проходит сквозной аварийный ток между точкой вход
и выход
схемы замещения, при условии, что в начальный момент времени все ее элементы находились в работоспособном состоянии.
Под простой по структуре схемой замещения системы будем понимать такую, элементы которой могут соединяться: последовательно, параллельно, последовательно-параллельно, либо параллельно-последовательно.
Под сложной по структуре схемой замещения системы будем понимать такую, в состав которой входит хотя бы одна группа элементов, соединенных в виде логической звезды
или треугольника
.
Элементы с тремя несовместными состояниями: работоспособное, отказ типа обрыв цепи
и отказ типа короткое замыкание
можно выделить в системах: электроснабжения, газоснабжения, водоснабжения и т.д. Аналогами элементов с тремя несовместными состояниями в таких системах могут быть защитные коммутационные аппараты, краны, вентили различных типов, запорная арматура, заглушки и другие виды прерывателей потока (электроэнергии, газа, жидкости, информации и т.д.), для которых в неработоспособном состоянии поток не прерывается (короткое замыкание
) или не передается (обрыв цепи
) [3].
В тех случаях, если необходимо повысить надежность проектируемой системы без изменения надежности комплектующих ее элементов обычно вводят избыточные (резервные) элементы, либо изменяют структурную схему сети. Для систем, состоящих из элементов, которые могут находиться в трех несовместных состояниях, введение избыточных элементов с тремя состояниями может не только не увеличить ее надежность, но даже снизить. Все будет зависеть от соотношения между различными видами отказов элемента схемы, ее конфигурации и числа резервных элементов или их групп.
Поэтому разработка новых и усовершенствование существующих методов оценки надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях, является актуальной научной проблемой, решение которой позволит значительно повысить точность прогноза их надежности, как на этапе проектирования, так и на этапе реконструкции и эксплуатации.
Анализ последних исследований и публикаций
Пусть все рассматриваемые элементы из которых состоит система, могут отказывать независимо друг от друга; каждый элемент системы может находиться в трех несовместных состояниях: работоспособном, неработоспособном – отказ типа обрыв цепи
, неработоспособном – отказ типа короткое замыкание
; потоки отказов элементов (типа обрыв цепи
и типа короткое замыкание
) простейшие; пропускная способность элементов не ограничена так же, как и способность сдерживать поток энергии (электрического тока, жидкости, газа, информации и т.д.) независимо от количества короткозамкнутых элементов; после выхода из строя элемент не восстанавливается (не заменяется на новый) в рассматриваемый период времени [4].
Обозначим через pi вероятность безотказной работы i-го элемента системы, qoi – вероятность появления отказов в i-том элементе типа обрыв цепи
, а через qsi – вероятность появления отказов в i-том элементе типа короткое замыкание
. Эти три состояния составляют полную группу несовместных событий.

Индексы о
и s
в формуле (1) указывают на то, что учитываются повреждения элемента, которые приводят к отказам типа обрыв цепи
либо отказам типа короткое замыкание
соответственно.
В том случае, если элементы системы подвержены двум типам несовместных отказов: отказ типа обрыв цепи
и отказ типа короткое замыкание
, тогда вероятность его отказов в течении времени t можно определить следующим образом [5]:


где λoi, λsi – постоянные интенсивности отказов i-го элемента при учете его отказов типа обрыв цепи
и типа короткое замыкание
соответственно;
t – текущее время работы i-го элемента системы.
Интенсивность отказов i-го элемента системы:


где noi, nsi – число выявленных аварийных отключений i-го элемента системы при учете отказов типа обрыв цепи
и типа короткое замыкание
;
N – число однотипных элементов за которыми установлено наблюдение;
Т – время наблюдения за элементами системы.
Для невосстанавливаемой системы, элементы которой могут находиться в трех несовместных состояниях, справедлива формула [5]:

где R – вероятность того, что в течение времени t не произойдет такое случайное событие, в результате которого разрывается связь или проходит сквозной аварийный ток между точками входа
и выхода
схемы замещения;
Qo, Qs – вероятность того, что произойдет разрыв связи и пройдет сквозной аварийный ток между точкой вход
и выход
схемы замещения соответственно;
Ro – вероятность того, что в течении времени t не произойдет такое случайное событие, в результате которого разрывается связь между точкой вход
и выход
схемы замещения.
Для простой по определению схемы замещения системы, которая состоит из n логически последовательного соединения элементов, отказ типа обрыв цепи
любого из i, (i = (1÷n)) элемента приводит к разрыву связи между точкой вход
и выход
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность разрыва связи между точкой вход
и выход
Qo определим следующим образом:
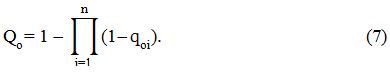
В том случае, если у каждого из n логически последовательно соединенных элементов произойдет отказ типа короткое замыкание
в каждом из i элементов, то это приведет к тому, что между точкой вход
и выход
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов элементов схемы замещения qsi, то вероятность Qs того, что между точкой вход
и выход
схемы замещения пройдет сквозной аварийный ток, найдем с помощью формулы:

Используя формулы (6-8), находим для системы, которая состоит из n логически последовательно соединенных элементов вероятность Rn того, что не произойдут такие случайные события, в результате чего разорвется связь или пройдет сквозной аварийный ток между точкой вход
и выход
схемы замещения:
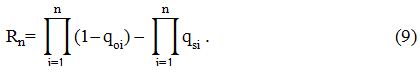
Для простой схемы замещения системы, которая состоит из m логически параллельно соединенных элементов, отказ типа обрыв цепи
в каждом из j
, (j = (1÷m)) элементе приводит к обрыву связи между точкой вход
и выход
.
Если заданы вероятности отказов элементов схемы замещения qoi, то вероятность Qo того, что произойдет разрыв связи между точкой вход
и выход
находим, пользуясь формулой:

В том случае, если у любого из m логически параллельного соединения элементов произойдет отказ типа короткое замыкание
, то это приведет к тому, что между точкой вход
и выход
схемы замещения пройдет сквозной аварийный ток.
Если заданы вероятности отказов qsi, (i = (1÷m)) элементов схемы замещения, которая состоит из m логически параллельного соединения элементов, тогда Qs – вероятность того, что между точкой вход
и выход
схемы замещения пройдет сквозной аварийный ток, найдем, используя формулу:

Подставив формулы (10-11) в формулу (6) находим, для системы, которая состоит из m логически параллельно соединенных элементов, вероятность Rm того, что не произойдут такие события, в результате чего рвется связь или проходит сквозной аварийный ток между точкой вход
и выход
схемы замещения:
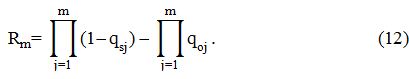
Формулы (9) и (12) справедливы при выполнении условия: qoi+qsi<1, qoj+Qsj<1 и получены различными способами [4].
Под сложной по структуре схемой замещения системы будем понимают такую, в состав которой входит хотя бы одна группа элементов, соединенных в виде логической звезды
или треугольника
.
Постановка задачи
Пусть задана сложная по структуре схема замещения системы (рис. 1):

Рисунок 1 – Сложная по структуре схема замещения системы, для оценки ее надежност
Элементы схемы замещения (рис. 1) могут находиться в трех несовместных состояниях: работоспособное; отказ типа обрыв цепи
и отказ типа короткое замыкание
.
Каждый элемент схемы замещения характеризуется вероятностями безотказной работы poi и вероятностями отказов qsi, (i = (1÷n)).
Следует определить вероятность R того, что за время t не произойдет разрыв связи или не пройдет сквозной аварийный ток между точкой вход
и выход
сложной по структуре схемы замещения, при учете двух несовместных видов отказов ее элементов, если в начальный момент времени все элементы системы находились в работоспособном состоянии.
Решение поставленной задачи
Задача состоит в том, чтобы сложную по структуре схему замещения (рис. 1) преобразовать в простую (по определению), а затем воспользоваться формулами (6-8), (10), (11) и определить R.
Для приведения сложной по структуре схемы замещения к простой (по определению) воспользуемся способом разложения сложной структуры по базовому элементу [6].
Этот способ преобразования сложной схемы замещения основан на использовании теоремы о сумме вероятностей несовместных событий.
Применительно к задачам оценки надежности систем электроснабжения, элементы которых могут находиться в трёх несовместных состояниях: работоспособное; отказ типа обрыв цепи
и отказ типа короткое замыкание
, эту теорему можно использовать следующим образом.
В сложной по структуре схеме замещения (рис. 1) выбираем базовый элемент i, обычно это тот, который соединяет между собой два ее узла.
Под узлом в схеме замещения будем понимать точку, которая соединяет между собой более двух линий.
Для схемы (рис. 1) делаем четыре допущения (а, б, в, г), что позволяет представить ее в виде двух схем (рис. 2 а, б).

Рисунок 2 – Способ разложения сложной схемы замещения (рис. 1) по базовому элементу i (учитываются отказы элементов схемы замещения системы типа обрыв цепи
и типа короткое замыкание
)
К схеме замещения сложной системы (рис. 1) предъявляют следующие допущения:
- Выбранный в схеме замещения системы базовый элемент i абсолютно надежен и пропускает через себя нагрузку потребителю (учитываются отказы элементов схемы замещения типа
обрыв цепи
). В соответствии с выдвинутым допущением в схеме замещения (рис. 1) выносится в последовательную с ней цепь базовый элемент i. В том месте схемы, где находили элемент i, ставится абсолютно надежная линия с неограниченной пропускной способностью, через которую нагрузка передается к потребителю электрической энергии. Элемент i в этом случае входит в схему замещения вероятностью безотказной работы роi (рис. 2а). - Выбранный в схеме замещения системы базовый элемент i абсолютно не надежен и пропускает через себя сквозной аварийный ток КЗ (учитываются отказы элементов схемы замещения типа
короткое замыкание
). Это означает, что в последовательную со схемой замещения системы (рис. 1) цепь выносится базовый элемент i. В том месте схемы, где находился элемент i, ставится абсолютно надежная линия с неограниченной пропускной способностью, по которой проходит сквозной аварийный ток. Элемент i в схему замещения (рис. 2а) входит вероятностью отказов qsi. - Выбранный в схеме замещения базовый элемент i абсолютно не надежен и не пропускает через себя нагрузку потребителю (учитываются отказы элементов схемы замещения типа
обрыв цепи
). В схеме замещения системы (рис. 1) выносим элемент i в последовательную с ней цепь и он характеризуется вероятностью отказов qoi. В том месте схемы замещения, где находился элемент i разрывается цепь (рис. 2б). - Выбранный в схеме замещения базовый элемент i абсолютно надежен и не пропускает через себя сквозной аварийный ток КЗ (учитываются отказы элементов схемы замещения типа
короткое замыкание
).
Выносится в последовательную со схемой замещения (рис. 1) системы цепь элемент i и он характеризуется вероятностью безотказной работы psi. В том месте схемы, где находился элемент i, разрывается цепь (рис. 2б).
В том случае, если полученные схемы замещения (рис. 2а, б) получились простыми, по определению, то используя формулы (7-8), (10-11) находим Ro1, Qs1 (рис. 2а) и Ro2, Qs2 (рис. 2б).
Используя теорему о сумме вероятностей несовместных событий находим вероятность Ro того, что связь между точкой вход
и выход
схемы замещения системы (рис. 1) не будет прервана, при условии учета отказов элементов схемы замещения типа обрыв цепи
:

Аналогичным образом определяется вероятность Qs того, что между точкой вход
и выход
схемы замещения (рис. 1) пройдет сквозной аварийный ток, при учёте отказов ее элементов типа короткое замыкание
:

Вероятность R того, что не произойдет разрыв связи или не пройдет сквозной аварийный ток между точкой вход
и выход
схемы замещения (рис. 1), находим используя формулы (6), (13), (14):

В том случае, если, например, при разложении сложной, по определению, схемы замещения по базовому элементу i получилось, что обе или одна схема оказались сложными по структуре, тогда для полученных сложных схем замещения выбирается новый базовый элемент и процедура их разложения продолжается до тех пор, пока все они не окажутся простыми.
Используя полученные простые по определению схемы замещения системы, формулы (7-8), (10-11), находим: Ro1, Ro2,...,Ron и Qs1,Qs2,...,Qsn (j = (1÷n)).
Полученные вероятности Roj и Qsj умножаются на соответствующие им вероятности безотказной работы (вероятности отказов) последовательно соединенных базовых элементов, которые соответствуют каждой из полученных простых по структуре схем.
Используя теорему о сумме вероятностей несовместных событий находим: Ro того, что связь между точкой вход
и выход
сложной схемы замещения системы не будет прервана, при учёте отказов ее элементов типа обрыв цепи
и вероятность Qs того, что между точкой вход
и выход
сложной схемы замещения пройдёт сквозной аварийный ток, при учёте отказов элементов схемы замещения типа короткое замыкание
.
Используя формулу (6) находим вероятность R того, что связь не будет прервана или не пройдет сквозной аварийный ток между точкой вход
и выход
сложной схемы замещения (рис. 1).
Из анализа формул (13) и (14) видно, что если получена формула для определения Ro вероятности того, что не произойдет разрыв связи между точкой вход
и выход
схемы замещения системы (учитываются отказы элементов схемы замещения системы типа обрыв цепи
), то формулу для получения вероятности Qs того, что между точкой вход
и выход
схемы замещения системы пройдёт сквозной аварийный ток (при учете отказов элементов схемы замещения типа короткое замыкание
) можно получить используя следующее правило: в формуле (13) производится замена Ro на Qs; вероятность безотказной работы i-го базового элемента (учитываются отказы элементов схемы замещения типа обрыв цепи
); poi заменяется на вероятность его отказов qsi (учитываются отказы элементов схемы замещения типа короткое замыкание
); вероятность отказов i-го базового элемента qoi заменяется на его вероятность безотказной работы psi; вероятность того, что не произойдет разрыв связи между точкой вход
и выход
простой схемы замещения Roj = f(po1,po2,...,pon) заменяется на вероятность того, что между точкой вход
и выход
простой схемы замещения пройдет сквозной аварийный ток, то есть на Qsj = f1(Qs1,Qs2,...,Qsn).
В результате произведенной замены получим формулу для нахождения Qs для любой сложной, по определению, схемы замещения [4].
Аналогичное правило соблюдается и для оценки надежности простых по определению схем замещения.
Сложные (по определению) схемы замещения системы можно приводить к одному эквивалентному по надежности элементу, используя формулы переходов от логического треугольника
к эквивалентной по надежности звезде
(рис. 3).

Рисунок 3 – Логическое соединение элементов в виде: а) треугольника
; б) звезды
Точные формулы переходов от логического треугольника
к эквивалентной по надежности логической звезде
(рис.3а, б) и от логической звезды
к эквивалентному по надежности логическому треугольнику (рис 3б, а) приведены в [3].
Для надежных систем, к которым относятся и электрические схемы, у которых qoi ≤ 0,1 и qsi ≤ 0,1, тогда произведениями вида: qox•qoy, qox•qoz, qoy•qoz, qox•qoy•qoz и qsx•qsy, qsx•qsz, qsy•qsz, qsx•qsy•qsz возможно пренебречь и тогда расчетные формулы можно значительно упростить.
Если заданы вероятности отказов элементов логического треугольника
(рис. 3а): qox, qoy, qoz, то эквивалентные вероятности отказов элементов звезды
qoi, qoj, qok находятся по формулам:

В том случае, если известны вероятности отказов qoi, qoj, qok элементов звезды
(рис. 3б), а необходимо получить эквивалентные вероятности отказов qox, qoy, qoz элементов треугольника
(рис. 3а), то в этом случае формулы примут вид:
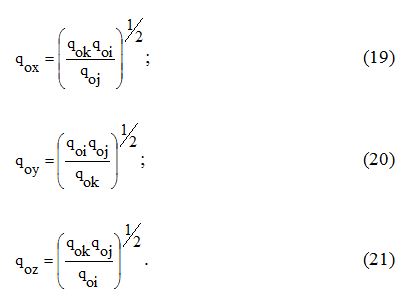
Аналогичные формулы получены и в [6].
Если заданы вероятности отказов элементов логического треугольника
(рис. 3а): qsx, qsy, qsz, то эквивалентные вероятности отказов логической звезды
qsi, qsj, qsk (рис. 3б) находим с помощью формул:
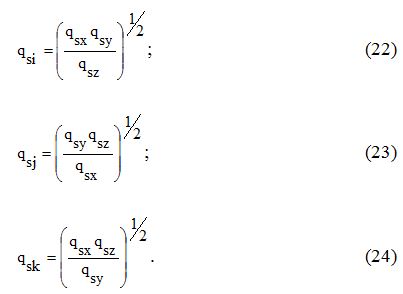
Если известны вероятности отказов qsi, qsj, qsk элементов логической звезды
(рис. 3б), а необходимо получить эквивалентные вероятности отказов элементов логического треугольника
(рис. 3а), то следует воспользоваться формулами:

Используя формулы (16-24) и (7,8), (10,11) можно любую сложную (по определению) схему замещения привести к одному эквивалентному элементу, а затем с помощью (6) определить R.
Для сложных по определению систем, элементы которых могут находиться в трех несовместных состояниях можно получить нижнюю оценку Rн, используя разработанную методику построения схем замещения минимальных сечений
с учетом двух несовместных типов отказов элементов (отказ типа обрыв цепи
и отказ типа короткое замыкание
) [7].
Пример
Задана схема замещения сложной системы (рис. 4). Для элементов схемы замещения заданы следующие интенсивности отказов: λo1 = 0,58 год−1; λs1 = 0,34 год−1; λo2 = 0,42 год−1; λs2 = 0,25 год−1; λo3 = 0,75 год−1; λs3 = 0,25 год−1; λo4 = 0,5 год−1; λs4 = 0,34 год−1; λo5 = 0,75 год−1; λs5 = 0,25 год−1; λo6 = 0,34 год−1; λs6 = 0,25 год−1; λo7 = 0,67 год−1; λs7 = 0,5 год−1; λo8 = 0,5 год−1; λs8 = 0,42 год−1.
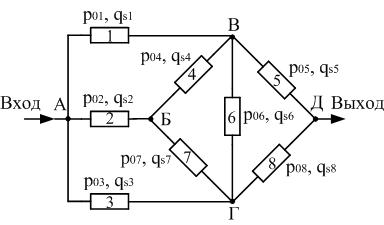
Рисунок 4 – Схема замещения сложной, по определению, системы
Определить вероятность R того, что не произойдет разрыв связи и не пройдет сквозной аварийный ток между узлами вход
и выход
схемы замещения в течение времени t = 0,1 год, используя следующие методы расчетов:
- Метод разложения сложной схемы замещения по базовому элементу, найти R(0,1).
- Метод преобразования логического
треугольника
в эквивалентную по надежностизвезду
и логическуюзвезду
в эквивалентный по надежноститреугольник
(приближенные формулы), найти R1(0,1). - Метод преобразования логического
треугольника
в эквивалентную по надежностизвезду
и логическуюзвезду
в эквивалентный по надежноститреугольник
(точные формулы) [3], найти R2(0,1). - Метод
минимальных сечений
[7], найти R3(0,1).
Каким образом изменятся: R(t), R1(t), R2(t), R3(t) при изменении t = 0,2÷1 год?
Решение. Используя формулы (2) и (3) исходные данные примера, для t = 0,1 год находим: qoi, qsi, (i = (1÷8)).
qo1 = 0,054; qs1 = 0,0325; qo2 = 0,0406; qs2 = 0,0242; qo3 = 0,0714; qs3 = 0,0238; qo4 = 0,0479; qs4 = 0,0326; qo5 = 0,0714; qs5 = 0,0238; qo6 = 0,033; qs6 = 0,0243; qo7 = 0,0632; qs7 = 0,0472; qo8 = 0,0478; qs8 = 0,0401.
В схеме замещения системы (рис. 4) в качестве базового элемента выбираем элемент 6. Схема (рис. 4) преобразуется в две новые (рис. 5а) и (рис. 5б). Из анализа полученных схем видно, что схема (рис. 5а) простая по структуре, а схема (рис.5б) – сложная (по определению).
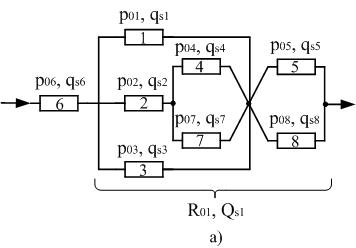

Рисунок 5 – Разложение сложной схемы замещения (рис. 4) по базовым элементам: 6, 4, 7
Для схемы (рис. 5б) в качестве базового элемента выбираем – 4, тогда она преобразуется в две новые (рис. 5в) и (рис. 5г). Анализ полученных схем показал, что схема (рис. 5в) сложная по структуре, а схема (рис. 5г) – простая.
В схеме замещения (рис. 5в) в качестве базового элемента выбираем элемент 7,тогда она преобразуется в две новые (рис. 5д) и (рис. 5ж) – простые по структуре схемы.
В результате разложения сложной по структуре схемы замещения (рис. 4) системы по базовым элементам 6, 4 и 7 получили четыре простые по структуре схемы замещения (рис. 5а, г, д, ж).
Используя полученные схемы замещения (рис. 5а, г, д, ж), формулы (13), (14), (15) и (7), (10), (8), (11) находим Ro, Qs и R:
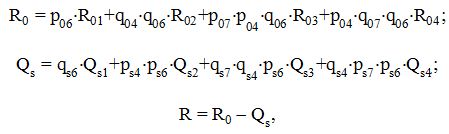
где

Подставив найденные значения qoi и qsi в полученные формулы, находим: Ro = Ro(0,1) = 0,9964; Qs = Qs(0,1) = 0,0018 (Qo = 0,0036) и R = R(0,1) = 0,9946).
Эта же задача была решена с использованием формул (16-27), (7,8), (10,11) и (6), в результате было получено: R = R(0,1) = 0,9946.
Решая исходную задачу, используя методику расчетов надежности систем, предложенную в [5], находим R2 = R2(0,1) = 0,9946.
Нижнюю оценку для R, т.е. Rн найдем, используя метод минимальных сечений
, предложенный в [7]. В этом случае Rн = R3 = R3(0,1) = 0,9946.
Результаты расчетов надежности исходной схемы замещения четырьмя методами приведены в таблице.
Таблица 1 – Определение: R(t), R1(t), R2(t), R3(t) при t = (0,2÷1)
| Ri(t) i = (1÷3) |
t, год | ||||
| 0,2 | 0,4 | 0,6 | 0,8 | 1 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| R(t) | 0,9791 | 0,9231 | 0,8435 | 0,7520 | 0,6581 |
| R1(t) | 0,9793 | 0,9246 | 0,8460 | 0,7546 | 0,6500 |
| R2(t) | 0,9795 | 0,9251 | 0,8475 | 0,7576 | 0,6646 |
| R3(t) | 0,9789 | 0,9215 | 0,8367 | 0,7349 | 0,6262 |
Из таблицы видно, в какой степени изменяется оценка надежности исходной системы, рассчитанная различными методами. В зависимости от степени важности системы и требуемой точности результата исследователь и выбирает методику расчетов.
Выводы
1. Используя способ разложения сложных структур по базовому элементу и теорему о сумме вероятностей несовместных событий, разработан точный метод оценки надежности невосстанавливаемых сложных (по определению) систем, элементы которых могут находиться в трёх несовместных состояниях (работоспособное; неработоспособное отказ типа обрыв цепи
; неработоспособное отказ типа короткое замыкание
).
2. Если в сложной (по определению) системе не учитывать отказы элементов типа короткое замыкание
, то для данного примера число аварийных отключений потребителей, которые получают электроэнергию от узла Д
, будет занижаться, для t = 0,1 год в 2 раза.
3. В том случае, если qoi(t) ≤ 0,1 и qsi(t) ≤ 0,1, то для оценки надежности сложных (по определению) систем можно использовать формулы (16-27).
Список использованной литературы
1. Козлов Б. А., Ушаков И. А. Справочник по расчету надежности аппаратуры, радиоэлектроники и автоматики. М.: Советское радио, 1975. – 472 с.
2. Беляев Ю. К. Надежность технических систем: Справочник / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. – М.: Радио и связь, 1985. – 608 с.
3. Ковалев А. П., Спиваковский А. В. О преобразовании звезда-треугольник
при расчетах надежности сложных по структуре систем. Электричество №10, 1998. – с. 70–74.
4. Ковалев А. П., Спиваковский А. В. Применение логико-вероятностных методов для оценки надежности структурно-сложных систем. Электричество №9, 2000. – с. 66–70.
5. Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем; Пер. с англ. – М.: Мир, 1984. – 318 с.
6. Голинкевич Т. А. Прикладная теория надежности. Учебник для ВТУЗов М.: Высшая школа, 1977. – 160 с.
7. Ковалев А. П., Москвина И. И. Расчет надежности невосстанавливаемых систем, элементы которых могут находиться в трех несовместных состояниях с. 165–174.
8. Ковалев А. П., Москвина И. И. Взрывозащищенное электрооборудование: сб. науч. тр. ГУ НИИВЭ
– Донецк: ООО Типография Восток Пресс
, 2017. – №1 (52) – 180 с.