Кумулятивный измеритель несинусоидальности напряжения

Авторы: Куренный Э. Г., Трейгер М.Б., Коломытцев А. Д.

Источник: Изв. ВУЗов. Электромеханика. – 1981. – № 2, c.187–1897

Воздействие электрических процессов на сеть и электроприемники обусловлены накоплением (кумуляцией) или отдачей энергии. Поэтому показатели качества напряжения (ПКН) должны быть кумулятивными, учитывающими не только величину, но и длительность воздействия. Опыт использования кумулятивных ПКН (отклонений [1–3] и колебаний [4] напряжения) показал, что все ПКН целесообразно определять на основе обобщенной динамической модели, состоящей из блока В воздействия и блока Э энергетической оценки. В статье рассматривается применение этой модели к оценке несинусоидальности напряжения.

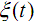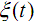Блок В преобразует напряжение u(t) или его искажения (помеху) u_п(t) в процесс , по которому судят о последствиях воздействия помехи. Блок Э определяет энергию процесса за заданное время 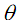. Как показано в [2–5], этот блок целесообразно выполнять в виде квадратора (или–приближенно– двухполупериодного выпрямителя) и линейного инерционного звена с постоянной инерции

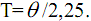
В связи с этим для применения модели необходимо решить следующие вопросы: какой аналог выбрать для блока В, чему равна постоянная инерции, как эквивалентировать помехи при наличии нормируемых ПКН.

Для практических целей достаточно определить коэффициент несинусоидальности (КНС) напряжения K_нс и увеличение 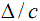тока I_C через конденсатор вследствие искажения синусоиды. В [6] нормируется величина

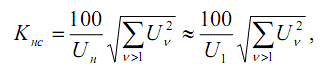
Допустимое значение КНС составляет 5%. В [7] увеличение тока ограничивается величиной 30%.

КНС (2) имеет смысл только для процессов, которые представляются в виде ряда Фурье. Но и для этих частных случаев величина оказывается неопределенной, так как сумма в (2) может быть отнесена к длительности, имеющей любую кратность по отношению к циклу основной частоты.

Подкоренное выражение в (2) по существу представляет энергию помехи за время цикла. Поэтому для устранения неопределенности [6] допустимость искажений будем оценивать по энергии процесса uп(t) за определенное время . В этом случае 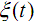= u_п(t), так что блок В представляет заграждающий основную частоту фильтр и безынерционное звено, аналогом которого служит активное сопротивление R. Такая динамическая модель применима для сетей и приемников с постоянным активным сопротивлением. Исследования по выбору типичного приемника не проводились, поэтому для определенности примем значение 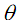. В этом случае 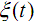=10 мин, указанное в [6] для отклонений частоты. Тогда согласно (1) постоянная инерции блока Э составит T_R = 4,45 мин.

По аналогии с терминологией [2–4] текущие значения выходного процесса 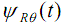назовем дозами несинусоидальности напряжения. Физический смысл дозы состоит в том, что она пропорциональна энергии искажений за предшествующий промежуток времени длительностью 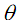. Дифференциальное уравнение, связывающее дозы с процессом после фильтра, в относительных единицах (о.е.) имеет вид:

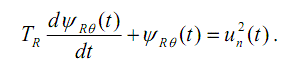
Доза имеет размерность (о.е.)². Для удобства в качестве ПКН примем кумулятивный КНС

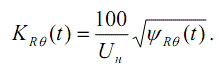
Уравнение (3) и кумулятивный КНС применимы для помех любого вида, а не только периодических. Вследствие большой длительности 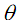, допустимость помехи можно оценивать по текущим максимумам выходного процесса. Условие эквивалентирования помех оказывается простым: помехи эквивалентны по 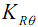, если максимумы на выходе модели одинаковы. Для частного случая периодических помех оценки согласно (2) и (4) совпадают, поэтому в качестве допустимого значения кумулятивного КНС естественно принять норму из [6], так что условие допустимости искажений имеет вид

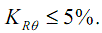
По смыслу оценки (5) и (2) неприменимы для конденсаторных установок. Например, при одной и той же допустимой величине 5%–ная гармоника более высокого порядка вызовет большее увеличение тока. Применительно к [7] в качестве блока В целесообразно выбрать конденсатор без фильтра. Величину 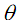примем из условия допустимого времени включения конденсаторной установки при 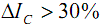, которое определяется выдержкой времени релейной защиты. С учетом [7], в среднем T_C = 100с.

Для идеального конденсатора емкостью С процесс на выходе модели связан с входным процессом дифференциальными уравнениями

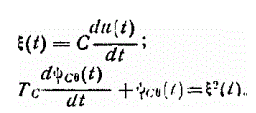
В реальных конденсаторах последствия ухудшения качества напряжения определяются потерями активной мощности. У неполярных диэлектриков емкость и 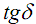не зависят от частоты [9], поэтому оценку искажений можно вести по полному току; который пропорционален активной составляющей тока. Кроме того, при постоянных С и 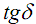, как и для идеального конденсатора, требования подобия выполняются для конденсаторов любой емкости и номинального напряжения. В общем же случае конденсатор является нелинейным звеном, что требует проведения специальных исследований для обоснования выбора структуры блока В.

Дозы тока через конденсатор выражаются в (о.е.)². В качестве ПКН удобно принять значения

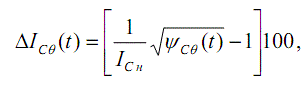
Условие допустимости имеет вид

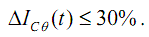
Дозы тока являются обобщенным показателем, так как изменения тока вызываются не только несинусоидальностыо, но и отклонениями напряжения основной частоты. Поэтому для выяснения причины увеличения тока следует измерять и КНС напряжения. В соответствии с рассмотренными моделями авторами был изготовлен и испытан в сетях Донбассэнерго кумулятивный измеритель несинусоидальности напряжения (КИНС). КИНС измеряет текущие значения КНС без осреднения и с осреднением согласно (3), а также текущие и осредненные значения тока через конденсатор. На шкале прибора нанесены предельные метки, соответствующие (5) и (7). Тарировку КИНС можно выполнять при любой частоте гармонического входного сигнала.

Выводы

1. Применение кумулятивных показателей несинусоидальности напряжения позволяет распространить требования ПУЭ и ГОСТ 13109–97 на любые виды помех, обеспечивая единство нормирования, расчета и измерения.
2. Комплексную оценку искажений синусоиды в действующих сетях рекомендуется выполнять с помощью кумулятивного измерителя несинусоидальности напряжения согласно (5) и (7).

Литература

1. Каялов Г. М., Каждаи А. Э., Ковалев И. Н., Куренный Э. Г. Основы построения промышленных электросетей.–М.: Энергия, 1978, 352 с.
2. Куренный Э. Г., Ковальчук В. М., Коломытцев А. Д. Оценка качества электроэнергии с использованием моделей объектов. – В сб.: Качество электроэнергии в сетях промышленных предприятий. Московский Дом научно–техн. Пропаганды им. Ф. Э. Дзержинского, 1977, с. 23–29.
3. Куренный Э. Г., Дмитриева Е. И., Треигер М. Б. Кумулятивный измеритель отклонений напряжения, там же. с. 49–54
4. Куренный Э. Г., Дмитриева Е. Н., Ковальчук В. М. Методы оценки электромагнитной совместимости группы электрических аппаратов.– 1978, с. 521–529.
5. Дмитриева П. Н. Расчет инерционных экстремумов электрической нагрузки группы электроприемников.–Изв. АН СССР. Энергетика и транспорт, 1979. № 4.
6. Нормы качества электрической энергии у ее приемников, присоединенных к электрическим сетям общего назначения. ГОСТ13109–97, 12 с.
7. >Правила устройства электроустановок. Раздел V.–Атомиздат, 2002, 48 с.
8. Свешников А. А. Прикладные методы теории случайных функций.–М.: Наука, 1968. 463 с
9. Ермуратский В. В., Ермуратский П. В. Конденсаторы переменного тока в тиристорных преобразователях. – М.: Энергия, 1979, 224 с.