МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СТРЕЛОВЫХ КРАНОВ ПРИ РАБОТЕ МЕХАНИЗМОВ ПОДЪЕМА И ИЗМЕНЕНИЯ ВЫЛЕТА

Е.Т. Ким (асп., каф. ПТСМ), А.Н. Орлов, д.т.н., проф.

Особенности современного экономического положения требуют создания конкурентоспособных машин в кратчайшие сроки, когда зачастую нет ни времени, ни средств на создание и испытания опытного образца в реальных условиях эксплуатации. Конструктор должен быть уверен, что произведенные им расчеты учитывают процессы, реально протекающие при работе крана. При этом надо иметь в виду, что процесс формирования модели для сложной динамической системы является трудной задачей, которую каждый раз приходится решать заново, как только исследователь сталкивается с новой конструкцией. В связи с этим создание обобщенных моделей и алгоритмов на их основе, пригодных для широкого класса кранов и их элементов, увеличивает возможность решения больших и практически важных задач.

Предлагаемая работа посвящена разработке математической модели стреловых кранов в виде механизмов с упругими звеньями при работе систем изменения вылета (СИВ) и подъема (СПД) на основе концепции, изложенной в работе [1].

При выводе дифференциальных уравнений, описывающих движение элементов СИВ и СПД крана с грузом, применен метод линеаризации уравнений движения механизмов с нелинейными функциями положения (каким является СИВ), основанный на предположении близости законов движения механизма с упругими звеньями к закону движения жесткого механизма. Закон движения СИВ в соответствии с жесткой динамической моделью принят за программный. Отклонения программного движения, вызванные податливостью звеньев элементов системы, рассматриваются как динамические ошибки и полагаются малыми величинами; в уравнениях движения членами, содержащими их второй порядок, пренебрегаем.

Для описания программного движения СИВ крана используются кинематические передаточные функции первого порядка, связывающие скорости звеньев крана с угловой скоростью стрелы. Выражения для кинематических передаточных функций получены для различных конструктивных исполнений стреловых систем, уравновешивающих устройств и механизмов изменения вылета, включая уравновешивающие устройства., расположенные под поворотной платформой. В процессе построения модели кинематические передаточные функции для гибкой модели линеаризируются в окрестности программного движения.

Используя уравнения Лагранжа второго рода, получим систему дифференциальных уравнений в матричном виде, описывающую движение элементов крана и груза при работе механизмов вылета и подъема:

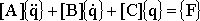
где {q} вектор обобщенных координат. Структура полученных матриц [A], [B] и [C] представляется в виде:

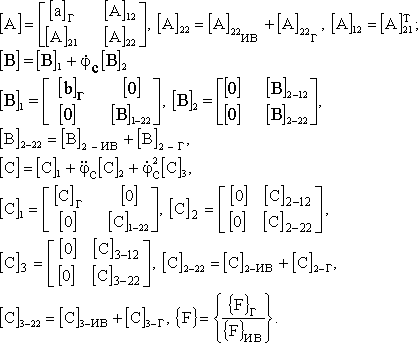
Все матрицы разбиты на блоки в соответствии с разбиением вектора обобщенных координат {q}; порядок каждого из блоков (6X6). [а]_г и [c]_г представляют собой инерционную и квазиупругую матрицу груза на пространственном канатном подвесе. Элементы матрицы [c]_г для грейферных схем подвесов приведены в работе [2], для траверсной – в работе [3]. [b]_г - диссипативная матрица груза. Модель позволяет проводить исследования при любых схемах подвесов груза, в том числе и при возможных ослаблениях подъемных канатов.

Матрицы [A] [B]₁ и [C]₁ - соответственно инерционная, диссипативная и квазиупругая - симметричные матрицы, элементы которых зависят от угла наклона стрелы и при фиксированном вылете постоянны. Это обстоятельство дает возможность использовать модальные методы исследования [4]. При изменении конструктивных исполнений СИВ в формулах для определения элементов матриц изменяются выражения для кинематических передаточных функций.

Литература

1. Орлов А.Н. Общая динамическая модель грузоподъемных кранов // В сб. “Оптимизация параметров строительных и дорожных машин”.– Ярославль, изд-во Яросл. полит. ин-та, 1992. С.13–20.

2. Орлов А.Н., Синицын В.Ю. К расчету частот собственных колебаний грейфера на канатном подвесе // Исследование оптимальных металлоконструкций и деталей подъемно-транспортных машин. Вып. 6. Саратов, 1992. С.28–32.

3. Орлов А.Н., Тахаладзе Г.С. Автоматизированный выбор оптимальных размеров крановых канатных подвесов груза// В сб. “Автоматизация проектирования в машиностроении”.–Л., изд-во ЛПИ им. М.И. Калинина, 1987. С. 17–24.

4. Орлов А.Н. Поперечные колебания грейфера с учетом ослабления подъемных канатов// В сб. “Динамика, прочность и надежность технологических машин”.–Труды СПбГТУ, № 478. – 1998.–С. 48-51.

5. Бортяков Д.Е., Орлов А.Н., Шевелев А.Б. Расчет и анализ частотного спектра портальных кранов // В сб. “Подъемно-транспортные машины и оборудование”. Вып. 2. Тула, 1999. С. 27–33.