Аннотация
Построена математическая модель асинхронного двигателя и структура бездатчиковой системы векторного управления электроприводом, приводится пример ее реализации для прямого пуска реального двигателя при подключении к сети синусоидального напряжения
Основной текст статьи
Около половины вырабатываемой в мире электроэнергии преобразуется в установках с асинхронным электроприводом, при этом подавляющее большинство технологических процессов требует регулирования, которое при нерегулируемом электроприводе осуществляется в самом технологическом процессе (изменением угла атаки винта с регулируемым шагом, перемещением заслонок в компрессорах, насосах, вентиляторах и др.). В то же время известно [1], что при переходе к регулируемому асинхронному электроприводу можно достичь экономии свыше 50 % электроэнергии по сравнению с нерегулируемым приводом; поэтому задача более полного исследования физических процессов при регулировании, их математическое описание и последующая реализация в системах управления является весьма актуальной
Цель статьи – обосновать применение математического моделирования асинхронного двигателя (АД) в системах управляемого электропривода, разработать адекватную математическую модель АД на основе модели Парка – Горева.
Реализация векторного управления обычно требует измерения или вычисления значения вектора состояния двигателя. Применение для этой цели датчиков для измерения потокосцепления или частоты вращения ухудшает эксплуатационные показатели электропривода, а системы с непосредственным измерением состояния не получили развития и мало перспективны. Наилучшим способом оценки состояния АД является анализ по дифференциальным уравнениям, описывающим работу электропривода.
Полная управляемость электропривода возможна, если обеспечивается управление электромагнитным моментом двигателя [2]. Для этой цели можно применить векторное управление с ориентацией по вектору потокосцепления ротора. Функциональная схема электропривода с таким управлением имеет наименьшее число перекрестных связей, а выражения для момента и скорости асинхронного электродвигателя с короткозамкнутым ротором сравнительно просты. При этом регулирование скорости при стабилизации потокосцепления ротора наименее трудоемко.
Типовая структурная схема [2] универсального электропривода на базе асинхронного короткозамкнутого двигателя состоит из самого двигателя, преобразователя частоты, включающего инвертор тока или напряжения с широтно-импульсной модуляцией, датчиков тока, напряжения, скорости и микропроцессорной системы управления
Для описания электромагнитных переходных процессов асинхронной машины необходимо составить уравнения электрического и механического равновесия, а также уравнение преобразования электромагнитной энергии в механическую.
Запишем систему уравнений асинхронной машины в координатах d, q, 0. Так как магнитная система ротора совершенно симметрична, то свяжем с ротором оси d и q и введем независимые ортогональные оси dt и qt, которые вращаются независимо от ротора и статора с определенной скоростью. Приведем ее к форме Коши, которая удобна для решения численными методами [3].
Первоначально система содержит четырнадцать уравнений при четырнадцати неизвестных: шесть составляющих токов, шесть составляющих потокосцеплений, электромагнитный момент и скорость вращения. Трудности решения такой системы связаны с присутствием в уравнениях периодических коэффициентов, поэтому система уравнений трехфазной асинхронной машины, записанная в реальных фазных величинах токов и потокосцеплений, преобразуется, в результате чего удается получить систему уравнений с постоянными коэффициентами. Оси d и q неподвижны относительно ротора и вращаются относительно статора со скоростью ротора
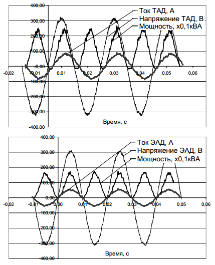
Рисунок 1 – Зависимости: частоты вращения ротора от времени (а), электромагнитного момента от времени (б), тока статора в фазе А от времени (в); механическая характеристика асинхронного двигателя (г)
Выводы
- Показана перспективность разработки бездатчиковых систем векторного управления асинхронным двигателем.
- Отсутствие датчиков компенсировано математическим моделированием АД.
- Разработанная математическая модель асинхронного двигателя еще не совершенна, но достаточно адекватна и может быть рекомендована к использованию в системах бездатчикового векторного управления.
Список использованной литературы
- Бичай В. Г. Состояние, тенденции и проблемы в области методов управления асинхронными двигателями / В. Г. Бичай, Д. М. Пиза, Е. Е. Потапенко // Радiоелектронiка, iнформатика, управлiння. — 2001. — №1. — С. 138 – 144.
- Усольцев А. А. Векторное управление асинхронными двигателями: Учеб.пособие по дисциплинам электромеханического цикла / А. А. Усольцев. — СПб.: Изд-во СПбГУИТМО, 2002. — 42 с.
- Ницай В. Е. Расчет динамических режимов судовых автоматизированных электроприводов / В. Е. Ницай. — Л.: Судостроение, 1970. — 192 с.
- Копылов И. П. Математическое моделирование электрических машин: Учебник для вузов / И. П. Копылов. — М.: Высш. шк., 1987. — 248 с.