Аннотация
В этой статье исследуется базовая структура реактивных вспомогательных услуг на рынке электроэнергии, способы генерации реактивной энергии. В отличие от активной мощности реактивная мощность может генерироваться не только генераторами, но и компенсирующими устройствами. Компенсирующие устройства используются как источники реактивной мощности для оптимизации общего потокораспределения, учитывающего затраты на передачу. Опыт показал, что их использование может уменьшить потери в линиях, стоимость реактивной мощности и улучшить уровень напряжения в распределительной сети.
Ключевые слова: рынок электроэнергии; производители распределенной энергии; умная распределительная сеть; оптимизация реактивной мощности.
Введение
Оптимизации реактивной мощности возможна в рамках традиционной электротехнической промышленности, и она отвечает интересам как поставщиков энергии, так и сетевой корпорации, поскольку они преследуют общую экономическую цель. Однако, в интеллектуальных сетях с изменяющимися нормативными и экономическими характеристиками, компенсирующие устройства в качестве поставщиков реактивной мощности сетевой корпорации принадлежат различным частным лицам, которые имеют свои собственные интересы.
Следовательно, реактивная мощность не вспомогательный, а потребительский продукт, такой как активная мощность, которая должна быть приобретена на рынке. Поэтому на рынке конкурентной энергии необходима оптимальная модель распределения реактивной мощности, которая учитывает стоимость вспомогательного обслуживания и надежность работы.
Оптимальные модели на рынке электроэнергии можно разделить на две категории: ценообразование вспомогательных услуг на генерацию реактивной мощности; экономическое распределение реактивной мощности с учетом ее стоимости, о которой идет речь в данной статье. Технические проблемы исследованы в рамках работ [2,3], включая управление частотой, поддержание напряжения и различные вспомогательные услуги. Оптимальная модель распределения реактивной мощности, направленная на минимизацию эксплуатационных затрат, предлагается в [4,5]. Она анализирует стоимость реактивной работы обычных генераторов, двунаправленных индукционных генераторов (DFIG) и фотоэлектрических генераторов (PV).
В предыдущей статье основное внимание уделялось анализу стоимости различных типов распределительных генераторов и игнорировалось влияние рынка на цену реактивной мощности. В этой статье, мы изучаем оптимальную модель, учитывающую стоимость реактивной мощности, потери в линиях и изменение напряжения, созданную для максимизации совокупных экономических выгод для сетевой корпорации.
Значение реактивной мощности на вспомогательном рынке электроэнергии
Рынок говорит, что система должна покупать компенсирующие устройства, для производства или потребления реактивной энергии. Устройства должны отвечать потребности в нормализации напряжения и реактивной мощности при работе сети.
Сначала, на рынке, производителями электроэнергии, проводится анализ затрат различных потребителей для получения ценовой функции производимой и потребляемой реактивной мощности в течение торгового периода. Затем, результаты загружаются в торговый центр Электрический рынок
, который рассматривает цену торгов от минимальной до максимальной, формируя кривую конкурентных ставок системы при разных уровнях мощности, как показано на рис. 1. Наконец, определяются цены производства, для каждой торговой сессии, в соответствии с потребностью в реактивной мощности.
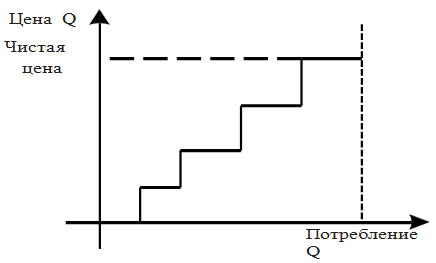
Рисунок 1 – Кривая цен реактивной мощности
Оптимизация распределения реактивной мощности
- Минимизация затрат на оплату активной и реактивной мощности
- Минимизация отклонения напряжения
- Ограничения потока:
- Ограничения неравенства:
- Метод решения
Оптимизация на рынке электроэнергии должна учитывать затраты на оплату реактивной мощности, таким образом, чтобы увеличить общую экономическую эффективность, которая сведет к минимуму стоимость реактивной мощности, потери мощности и стоимость устройств компенсации:
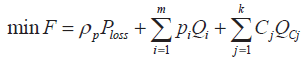
(1)
где ρρ – активная предельная цена, Ploss – потери мощности, pi – чистая цена за реактив, Qi – реактивная мощность от i-го DPP, m – количество DPP, Cj – это затраты на компенсацию реактивной мощности j-й параллели конденсатора, QCj – компенсационная емкость j-й параллели конденсатора, k – количество установленных параллельно конденсаторов.
Состоит в том, чтобы свести к минимуму сумму отклонений напряжения каждого узла, заставляя систему работать в нормальном состоянии, функция имеет вид:
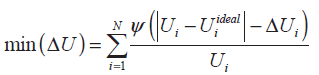
(2)
где:
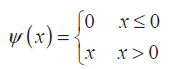
(3)
где N – общее количество узлов; Ui – значение напряжения узла i; Uiideal – желаемое напряжение узла i; ΔUi – максимально допустимое отклонение напряжения узла i; примем Uiideal = 1, ΔUi = 3 %.

(4)
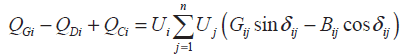
(5)
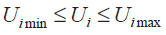
(6)

(7)
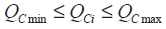
(8)
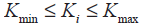
(9)

(10)
где Pi, Qi – соответственно активная и реактивная мощность узла i; Gij, Bij, δij соответственно являются проводимостью, восприимчивостью и разностью фазового угла между узлом i, j; Ui max, Ui min – предельные напряжения узла; QG min, QG max – верхний и нижний пределы реактивной мощности DG, предоставляемые DPP на основе прогнозируемого значения; QC min, QC max – пределы исходной мощности компенсирующих установок; Ki min, Ki max – это предельные положения отпаек для устройства РПН; Lemax – максимально допустимый ток линии.
Модель оптимизации реактивной мощности, построенная в разделе, относится к проблеме многоцелевой оптимизации с ограничениями, для которых нет наилучшего решения, так как все варианты одновременно оптимальны, поэтому оптимальное решение может выбираются лицами, принимающими решения, исходя из различных подцелей [7]. Для выбора модели используется сортировочный алгоритм-Ⅱ (NSGA-Ⅱ). Он позволяет потребителям анализировать и изменять положения рынка.
Тематическое исследование
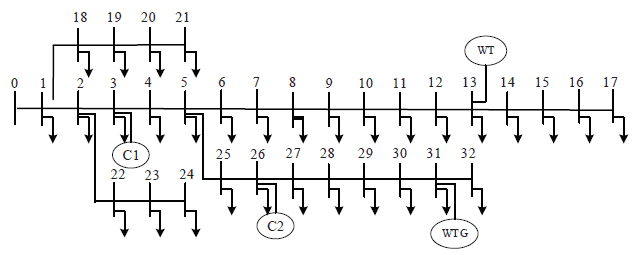
Рисунок 2 – Система распределения узлов IEEE33
Рынок реактивной мощности включает в себя WT, PV, микрогазовые турбины и конденсаторные батареи. WT и MGT расположены на шинах 13 и 31, каждый с номинальной мощностью 300 кВт. Банки шунтирующих конденсаторов расположены на шинах 3 и 26, каждый с номинальной мощностью 300 квар. Каждый банк шунтирующих конденсаторов содержит 30 комплектов конденсаторов.
План оптимизации реактивной мощности основан на результатах активного планирования. Приняв активную предельную цену как 200 юаней / (МВт×ч), реактивные данные о ценах ветровых турбин и микротурбин взяты из литературы [9], данные диапазона выходных реактивных мощностей взяты из литературы [10].
Для решения оптимизационной модели применяется програмирование в MATLAB, а параметры NSGA-II устанавливаются следующим образом: численность населения 50; максимальное число итераций – 200; коэффициент кроссинга равен 0,8; скорость изменения составляет 0,3.

Рисунок 3 – Фаза Парето, рассчитанная NSGA-Т
Анализ результатов
Паретовое распределение алгоритма NSGA-II является однородным и стабильным, в результате проверяется осуществимость алгоритма. Горизонтальная ось на рис.4 представляет собой комплексную стоимость распределительной сети, а вертикальная ось – отклонение напряжения. Когда компенсирующие устройства генерируют больше реактивной мощности, напряжение в сети повышается, а потери снижаются. Как видно из рисунка выше, общая стоимость электроэнергии снижается по мере увеличения напряжения.
Использование распределенной генерации при оптимизации реактивной мощности в распределительной сети выгодно для уменьшения потерь активной мощности и повышения уровня напряжения в сети.
В табл. 1 показаны реактивные мощности WT, MT и двух групп конденсаторов, соответствующие самой близкой точке от источника на рис. 2. В табл. 2 приведено сравнение результатов до и после оптимизации в соответствии с вышеприведенными параметрами.
| Единица | WT | MT | C1 | C2 |
| Q | 0,0960 | 0,0759 | 0,27 | 0,29 |
| Ploss / MW | DGC / ¥ | RDC / ¥ | U / pu. | |
| До | 0,26 | - | - | 0,23 |
| После | 0,18 | 3,7 | 2,6 | 0,29 |
Как видно из табл. 2, потери мощности снижаются на 31 %, а напряжение повышается на 26 %. Стоимость до и после оптимизации составляет соответственно 52 и 42,3 юаней, что указывает на то, что текущая стоимость распределенной сети снижается. Таким образом, мы можем сказать, что модель, предложенная в этой статье, справляется со своими задачами.
Выводы
В этой статье изучается базовая структура рынка вспомогательных услуг реактивной мощности, в перспективе всего рынка страны, для изучения возможности стимулирования децентрализованных компенсаторов принимать участие в оптимизации распределения реактивной мощности. Исходя из этого, оптимальная модель снабжения реактивной мощностью интеллектуальной распределительной сети устанавливается в условиях конкурентного рынка электроэнергии. Результаты моделирования показывают, что при планировании оптимизации распределения реактивной мощности, на рынке, можно учитывать интересы, как энергосистемы, так и производителей электроэнергии. При этом, благодаря регулировке реактивной мощности компенсирующими устройствами, эксплуатационные расходы сети могут быть уменьшены, а уровень напряжения улучшен.
Список литературы
1. Alsokhiry F, Adam G P, Lo K L. Contribution of distributed generation to ancillary services
. Universities Power Engineering Conference (UPEC), 2012 47th International, pp.1-5, 2012.
2. Porter D, Strbac G, Mutale J. Ancillary service provision from distributed generation
. Electricity Distribution, 2005. CIRED 2005. 18th International Conference and Exhibition on, pp. 1-4, 2005.
3. Kotsampopoulos P, Hatziargyriou N, Bletterie B, Lauss G. Review, analysis and recommendations on recent guidelines for the provision of ancillary services by Distributed Generation
. Intelligent Energy Systems (IWIES), 2013 IEEE International Workshop on, pp. 185-190, 2013.
4. Haghighat H, Kennedy S. A model for reactive power pricing and dispatch of distributed generation
. Power and Energy Society General Meeting, 2010 IEEE, pp. 1-10, 2010.
5. Kolenc M, Papic I, Blazic B. Coordinated reactive power control to achieve minimal operating costs
. International Journal of Electrical Power & Energy Systems, vol. 63, pp. 1000-1007, 2014.
6. Rueda-Medina A C, Padilha-Feltrin A. Distributed generators as providers of reactive power support-a market approach
. Power Systems, IEEE Transactions on, vol. 28(1), pp. 490-502, 2013.
7. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multi-objective genetic algorithm: NSGA-II
. IEEE Trans on Evolutionary Computation, vol. 6(2), pp. 182-197, 2002.
8. Zhang Lu, Tng Wei, Cong Pengwei, Bai Muke, Suo Li Optimal configuration of generalized power sources in distribution network based on chance constrained programming and bi-level programming
. Automation of Electric Power Systems, vol. 38(5), pp. 50-58(in Chinese), 2014.
9. Madureira A G, Lopes J A P. Ancillary services market framework for voltage control in distribution networks with microgrids
. Electric Power Systems Research, vol. 86, pp. 1-7, 2012.
10. Tan Huang, Zhang Lu, etc. Day-Ahead reactive power scheduling for distribution network considering coordination of distributed generation with capacitors
. Power System Technology, vol. 9, pp. 2590-2597, 2014.