Оптимальное управление потоками мощности в неоднородных электрических сетях с дальними электропередачами

Ключевые слова: электрическая система, дальние электропередачи, неоднородность, общесистемный показатель неоднородности, условия оптимальности, оптимальное управление.

Введение

Одним из основных показателей эффективности использования электроэнергии являются технологические расходы, связанные с ее транспортировкой от источников питания к потребителям. Анализ фактических расходов электроэнергии в Украине в последние годы [1] свидетельствует о превышении соответствующих показателей, свойственных странам Западной Европы. Особенно это касается распределительных электросетей, для которых, кроме конструктивного несоответствия современным условиям эксплуатации, характерно негативное влияние со стороны магистральных электросетей, обусловленное их неоднородностью [2,3].

Главной причиной повышенного расхода электроэнергии, в частности технической составляющей потерь, является низкая эффективность электросберегающих мероприятий, что, в свою очередь, обусловлено недостаточным уровнем автоматизации контроля и управления режимами магистральных и распределительных электросетей. Учитывая высокий уровень развития современных микропроцессорных систем и широкомасштабное внедрение автоматизированных систем мониторинга режимов, особенно магистральных электросетей, становится возможным, во-первых, использовать информацию из баз данных таких систем в задачах оптимизации управления потоками мощности [3] и взаимовлияния [4] электрических сетей в электрической системе (ЭС) [4], а во-вторых, интегрировать подсистемы автоматизации оптимального управления в состав автоматизированной системы диспетчерского управления (АСДУ).

Автоматизация оптимального управления потоками мощности в современных ЭС, развиваясь на базе существующих АСДУ, предусматривает разработку и усовершенствование технического, информационного и программного обеспечения. На сегодняшний день в практике диспетчерского управления энергосистемами используют программно-технические средства оптимизации нормальных режимов ЭС, которые имеют ряд недостатков. Несовершенство математически-программного обеспечения обусловлено, преимущественно, с использованием упрощенных математических моделей процессов транспортировки электроэнергии, которые были актуальными 20–30 лет назад и не соответствуют современному уровню аппаратного обеспечения. В составе аппаратного обеспечения, несмотря на его всестороннее развитие, которое наблюдается в последнее время, практически отсутствуют специализированные информационные устройства связи между регулирующими устройствами ЕС (трансформаторов и автотрансформаторов с РПН и др.) и управляемыми электронно-вычислительными машинами (ЭВМ). А без таких устройств невозможно взаимодействие программных средств оптимального управления режимами электрических сетей и регулирующих устройств (РУ). Кроме того, автоматизированные системы, обеспечивающие локализацию отдельных функций централизованного управления, реализуя программное управление с местными параметрами и оперативную коррекцию наладочных параметров локальных систем автоматического управления (САУ), способны повысить надежность функционирования системы в целом и расширить ее функциональность в особых режимах работы.

Следовательно, вопросы совершенствования программно-аппаратного обеспечения АСДУ ЭС в направлении реализации оптимального управления их нормальными режимами за счет развития математических моделей и методов оптимизации параметров РУ, а также средств реализации таких параметров являются актуальными.

Обобщенные показатели неоднородности ЭС

Негативное влияние неоднородности электросетей на оптимальность распределения мощностей в ЭС может быть описано фиктивными уравнительными э. д. с. E_ур, которые приводят к появлению в замкнутых контурах уравнительных токов и, таким образом, к отклонению реального токораспределения I от экономического I_эк [2,3]. Для неоднородных электросетей, содержащих трансформаторные связи и длинные электропередачи, э. д. с. можно определить по выражению [6]:

E_ур = N_Ak Z_B (I − I_эк),(1)

где N_Ak – матрица связей веток ЭС в ее контурах, построенная с учетом трансформаторных связей и дальних электропередач [6]; Z_B – диагональная матрица сопротивлений ветвей схемы замещения [6], в которой ветки дальних передач представлены постоянными четырехполюсника В [5,6]; I_эк – вектор экономических токов в ветвях схемы замещения электросетей, определенный на основании расчета экономического режима электросетей с дальними ЛЭП; I – вектор токов в ветвях, что соответствует реальному токораспределению с учетом взаимовлияния электросетей различных классов напряжения, которые работают параллельно.

В [6] показано, что токораспределение с минимально возможными потерями мощности в ЭС с дальними ЛЭП, которое соответствует экономическому режиму работы электросетей [2], может быть рассчитано по r-схеме замещения ЭС (по аналогии с [3]) при таких условиях:

• в схеме замещения учтены активные сопротивления элементов с сосредоточенными параметрами (коротких ЛЭП, трансформаторов и т. п.) и действительные части постоянных четырехполюсников В (для дальних ЛЭП);
• коэффициенты трансформации в замкнутых контурах принимаются сбалансированными (отсутствуют э. д. с. небаланса);
• коэффициенты распространения волны γ₀ [5,7] и длины ЛЭП l соотносятся так, что в замкнутых контурах с дальними ЛЭП не возникает э. д. с. небаланса (постоянные четырехполюсника A_i = ch(γ_0il_i) = idem).

Исходя из приведенного, выражения для определения векторов I и I_эк как функций задающих токов J в узлах схемы замещения ЭС могут быть представлены так:

I = Z_B⁻¹M^T_Ak (M_AkZ_B⁻¹M^T_Ak)⁻¹ (J − Y_бU_б) + Z_B⁻¹M^T_бU_б;(2)

I_eк = R_B⁻¹M'^T_Ak (M'_AkR_B⁻¹M'^T_Ak)⁻¹ (J − Y'_RбU_б) + R_B⁻¹M'^T_бU_б,(3)

где M_Ak = M⁺ + M⁻A_дK – матрица связей веток электрической сети в ее узлах с учетом идеальных трансформаторов и дальних электропередач [3,6]; M^T_Ak = M^T+ + KA_дM^T− – транспонированная матрица связей веток электрической сети в ее узлах (символ «Т» здесь и далее обозначает операцию транспонирования матриц); M^T+, M^T− – матрицы, которые формируются заменой, соответственно, отрицательных или положительных элементов транспонированной матрицы соединений M^T [2] нулями; K, K, A_д – диагональные матрицы, соответственно, прямых и комплексно-сопряженных коэффициентов трансформации трансформаторных ветвей и постоянных четырехполюсника А для других веток схемы замещения электрической сети; Y_б, Y_Rб – столбцы матрицы узловых проводимостей, соответствующих базисному узлу электрической сети, определенные, соответственно, по полной схеме замещения и по r-схеме; U_б – напряжение базисного узла электрической сети; M^T_б – столбец матрицы соединений соответствует базисному узлу электрической сети; R_B – диагональная матрица сопротивлений ветвей, содержащая только активные составляющие сопротивлений веток Z_B; M'^T_Ak, M'_Ak, M'^T_б,Y'_Rб – матрицы связей и пассивных параметров схемы замещения ЭС, определенные с учетом условий расчета экономического режима, которые представлены выше.

Подставив в (1) выражения для I и I_эк, после преобразований и упрощений получим:

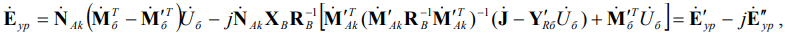
(4)

где X_B – диагональная матрица сопротивлений ветвей, содержащая только реактивные составляющие сопротивлений веток Z_B.

По определению, матрицы-столбцы M^T_б = M'^T_б, т. е. составляющая E' = 0. Следовательно, (4) можно представить в виде:

(5)

или в относительных единицах в приведении к напряжению базисного узла:

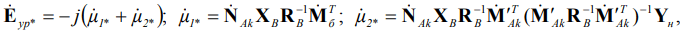
(6)

где Y_н = (JU_б⁻¹ − Y'_Rб) – вектор проводимостей нагрузок с учетом взаимных проводимостей базисного узла. Векторы μ_1*, μ_2* определяются соотношением реактивных и активных сопротивлений ветвей схемы замещения электрической сети, коэффициентами трансформации трансформаторов и постоянными четырехполюсника дальних ЛЭП А, то есть являются обобщенными показателями неоднородности электрической сети. Исходя из (6), отсутствие уравнительных э. д. с. в замкнутых контурах характерно только для электрических сетей, в которых все ветки соответствуют классическому условию однородности [2] x_i / r_i = idem (необходимое условие – μ_2* = 0), а коэффициенты трансформации в контурах сбалансированы и для дальних ЛЭП обеспечивается условие согласованности коэффициентов распространения волны 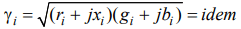[5] (достаточное условие – μ_1* = 0). Исходя из последнего, обеспечить однородность электросетей с дальними ЛЭП проектными мероприятиями практически невозможно, особенно учитывая существенную зависимость их поперечных проводимостей g_i, b_i от случайного воздействия окружающей среды. Для обеспечения режимов их работы, близких к экономическим, целесообразно применять меры по оптимальному управлению трансформаторами связи с продольно-поперечным регулированием.

Метод формирования законов оптимального управления потоками мощности в электрических системах на основании анализа их неоднородности

Как известно [3], компенсировать дополнительные потери мощности и электроэнергии в ЭС, обусловленные ее неоднородностью [2,3], можно путем регулирования напряжения в узлах ЭС или введением в контуры уравнительных э. д. с. При такой постановке задачи управляемыми переменными являются э. д. с, которые необходимо ввести в замкнутые контуры для реализации оптимального токораспределения [3] за счет изменения коэффициентов трансформации трансформаторов, входящих в эти контуры.

В [3] показано, что оптимальное значение потерь в ЭС достигается при относительных значениях э. д. с., которые рассчитывают по формулам:

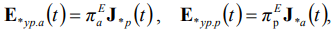
(7)

где E_*ур.a(t), E_*ур.р(t) – векторы активных и реактивных составляющих относительных значений уравнительных э. д. с.; J_*a(t), J_*р(t) – векторы активных и реактивных составляющих относительных значений токов в узлах ЕС; – вектор узловых токов ЕС (символ «^» здесь и далее обозначает комплексно-сопряженные значения комплексных величин); U_д(t), S(t) – диагональная матрица узловых напряжений и вектор узловых мощностей; π^E_а, π^E_p – матрицы критериев подобия.

В (7) все параметры поданы в относительных единицах. Как базисные принимаются параметры идеального режима, рассчитанного по r-схеме замещения ЭС.

Матрицы критериев подобия определяют по формулам [3]:

(8)

где – матрица системных показателей неоднородности ЭС; r_к, x_к – активная и реактивная составляющие матрицы контурных сопротивлений для системы базисных контуров; М_α, N_α – матрицы соединений веток дерева схемы замещения ЭС, соответственно, в узлах и контурах.

Соотношения (7) являются законами оптимального управления, в которых коэффициенты обратной связи по физическому смыслу – критерии подобия. Для реализации законов управления согласно (7) разработана система автоматического управления (САУ) нормальными режимами ЭС [3,4], основная функция которой заключается в том, чтобы поддерживать значение комплексного критерия оптимальности F^*, в котором учтены факторы надежности и экономичности транспортировки электроэнергии, а также ее качества [3,4], в пределах установленной зоны нечувствительности δF^* (управляющие воздействия регулирующими устройствами осуществляются после выхода критерия за ее пределы). Результатом действия системы является приближение текущей траектории изменения потерь мощности в ЭС к оптимальной по заданным эксплуатационным условиям [3]. Кроме того, как показано в [4], реализация управляющих воздействий, полученных на основании (7), обеспечивает оптимизацию взаимовлияния магистральных и распределительных электросетей по потерям и уровням напряжений.

Однако для получения (7) и (8) был использован ряд допущений. Приведение параметров электросетей с трансформаторными связями к одному классу напряжения и, соответственно, невозможность учета несбалансированных коэффициентов трансформации в контурах ЭС, расчет емкостного генерирования и потерь на корону для линий электропередачи (ЛЭП) с номинальными напряжениями, моделирование режимов дальних ЛЭП без учета их волновых свойств могут негативно влиять на адекватность воспроизведения оптимальных состояний ЭС и вызывать принятие и реализацию неэффективных решений.

Совершенствование метода формирования законов оптимального управления нормальными режимами электрических систем с дальними электропередачами

Для компенсации негативного влияния неоднородности параметров электросетей ЕС за счет управления РУ в контуры необходимо ввести э. д. с. небаланса E_нб → −E_ур, за счет чего токи небаланса I_нб частично или полностью компенсируют фиктивные уравнительные токи I_ур [3]. В общем случае для j-го контура, принадлежащего таким образом системе базисных контуров [2,3], э. д. с. небаланса определяют:

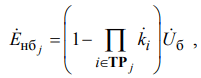
(9)

где k_i – коэффициент трансформации i-го трансформатора, принадлежащий множеству трансформаторов j-го контура ТР_j; U_б – напряжение базисного узла ЭС.

Фиктивные уравнительные э. д. с. в неоднородных электросетях, содержащие трансформаторные связи и дальние электропередачи как функции природного и экономического токораспределения, можно определить по выражению (1). Выражения для определения векторов (3) при наличии нескольких балансирующих узлов в электросетях могут быть представлены следующим образом [6]:

(10)

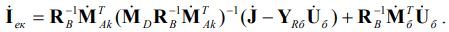
(11)

Подставив в выражение уравнительных э. д. с. (1) выражения для I и I_эк, после преобразований и упрощений получили:

E_зр = E_*нб.kU_б – j(E_*нб.γU_б + Z_ф.зрJ),(12)

где E_*нб.k = N_AkM^T_б – матрица относительных контурных э. д. с., которые определяются несбалансированными коэффициентами трансформации и коэффициентами распространения волны дальних ЛЭП (j-ый элемент E_*нб.j соответствует выражению (9)); – матрица относительных контурных э. д. с., которая определяется перетоками мощности между балансировочными источниками электроэнергии ЭС и зависит от неоднородности системы; – матрица фиктивных контурных сопротивлений определяет уравнительные э. д. с. как функцию неоднородности продольных и поперечных параметров ЭС.

Из (12) видно, что составляющие E_*нб.γ и Z_ф.ур определяются соотношением реактивных и активных сопротивлений ветвей схемы замещения ЭС, коэффициентами трансформации трансформаторов и коэффициентами распространения волны дальних передач (в виде постоянных четырехполюсника А). Следовательно, как показано выше, отсутствие уравнительных э. д. с. в замкнутых контурах характерно только для электросетей, в которых коэффициенты трансформации в контурах сбалансированы, все ветки соответствуют классическому условию однородности [2], а для дальних ЛЭП обеспечивается условие согласованности коэффициентов распространения волны. Исходя из последнего обеспечить однородность электросетей с дальними ЛЭП практически невозможно, а для обеспечения режимов их работы, близких к экономическим, необходимо оптимальное управление трансформаторами связи с продольно-поперечным регулированием.

Для случая ЭС с единым базовым узлом E_*нб.γ = 0, а э. д. с. небаланса определяют только несбалансированными коэффициентами трансформации. Оптимальное корректирование указанных параметров РУ обеспечивает выполнение условия экономичности токораспределения в ЭС и, соответственно, перетоков мощности и взаимовлияния электросетей различных классов напряжения (E_ур → 0).

Если ставится задача оптимизации потокораспределения ЭС с несколькими балансировочными источниками электроэнергии, то к э. д. с. небаланса добавляется составляющая, определяемая перетеканием мощности между источниками E_*нб.γ U_б. Следовательно, компенсировать уравнительные э. д. с. в таком случае можно, кроме указанного выше, регулированием напряжения в центрах питания (изменением генерирования реактивной и активной мощности в ЭС).

Условие обеспечения экономического токораспределения E_ур = 0, исходя из (12) может быть представлено таким образом:

(13)

где – вектор оптимальных контурных э. д. с. небаланса, которые по физической природе могут быть реализованы изменением параметров РУ. Оптимальное значение коэффициента трансформации регулировочного трансформатора k₀^opt для j-го базисного контура, которое начинается с i-го базисного узла, исходя из (9), учитывая влияние коэффициентов распространения волны дальних ЛЭП [6], может быть рассчитано по выражению:

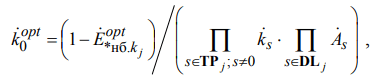
(14)

где A_s – постоянная четырехполюсника для s-й ЛЭП [6], что входит в множество дальних линий j-го контура DL_j.

Таким образом, используя выражения (13), (14), можно определить оптимальные коэффициенты трансформации регулирующих трансформаторов с учетом изменения нагрузки потребителей, планового генерирования источников электроэнергии, а также последствий первичного регулирования напряжения. В отличие от (7), в (13), (14) учитывается также влияние особенностей процесса транспортировки электроэнергии дальними ЛЭП, что повышает адекватность решений по оптимальному управлению нормальными режимами ЭС.

Особенности реализации системы автоматического управления потоками мощности в ЭС с децентрализацией функций управления в реальном времени

Для реализации системы автоматизированного управления потоками мощности и напряжением в электрических системах, которая обеспечивала бы возможности оперативного управления в соответствии с (13), (14), целесообразно использовать классическую двухконтурную схему [3,4] с децентрализацией функций управления в реальном времени. На первом этапе (в контуре централизованного управления) определяют причины неоптимального функционирования ЭС и перечень доступных регулирующих устройств. Для этого выполняют ретроспективный анализ результатов управления режимами на основании краткосрочного планирования, а также оценивают показатели неоднородности ЭС. Далее, используя полную информацию о параметрах ЭС, определяют и корректируют матрицы условно постоянных параметров, входящих в (13). С использованием разработанных [3,4] математических моделей осуществляют адаптацию законов управления в реальных условиях функционирования регулирующих устройств, выполняют ранжирование регулирующих устройств по приоритету управления с учетом надежности и ресурса устройств РПН. Определяют зоны нечувствительности локальных систем управления регулирующими устройствами, что позволяет установить рациональную интенсивность переключений для каждого трансформатора и скоординировать их работу во время оперативного управления таким образом, чтобы снижение потерь мощности достигалось при минимальном количестве переключений.

На втором этапе (в контуре локального управления) полученные математические модели (13) используют для определения расчетного значения управляющих воздействий (14) и принятия решения о целесообразности их реализации. Управление в темпе процесса осуществляют только в контуре оперативного управления. Во внешнем контуре, при необходимости, может осуществляться корректировка пассивных параметров ЭС для (13). Однако такое изменение чаще осуществляется на стадии краткосрочного планирования режимов после значительных изменений нагрузок или существенных отклонений параметров регулирующих устройств от плановых [4].

Подобная схема реализации системы управления позволяет обеспечить децентрализацию части информационных функций без потери принципов централизованного управления, поскольку в течение основного времени (режимы нормальной эксплуатации ЭС) регулирование параметров трансформаторов осуществляется на основании локальных параметров, обеспечивая условный оптимум общесистемного критерия оптимальности [3,8]. Отклонение пассивных параметров ЭС или параметров режима централизованно контролируют и при необходимости корректируют отдельные параметры моделей (13) и (14). Следовательно, по сути реализуется централизованное оперативное управление режимами ЭС с помощью децентрализированных подсистем – локальных регулирующих устройств на отдельных трансформаторных подстанциях (электростанциях).

Автоматическое управление РУ ЭС и согласование управляющих воздействий с оперативным управлением выполняют с использованием микропроцессорного устройства автоматического контроля и управления функционированием (АКУФ) РУ [8] (рис. 1). Устройство может работать в трех основных режимах:

1. получение закона с управляющей ЭВМ и управления согласно ему (при наличии в достаточном количестве достоверной информации о состоянии электрической сети);
2. введение из центральной системы управления номера отпайки и установки ее на регуляторе РПН трансформатора (при отсутствии должного информационного обеспечения или дистанционного управления диспетчером энергосистемы);
3. автономная работа устройства в режиме стабилизации вторичного напряжения трансформатора или автотрансформатора на заданном уровне с учетом введенной зоны нечувствительности, или автономная реализация встречного регулирования напряжения.

Рисунок 1 – Внешний вид устройства АКУФ РУ (вид спереди)

Для перевода АКУФ РУ из состояния ожидания в активное состояние средствами АСУ подстанции через блок связи передают код операции. После этого устройство проверяет параметры РПН для идентификации крайних положений: полученную информацию записывают в оперативное запоминающее устройство (ОЗУ). В зависимости от кода операции устройство переводят в соответствующий режим работы.

При необходимости установить определенную отпайку регулятора РПН сначала через блок связи осуществляют ввод ее номера от управляющей ЭВМ. В случае несовпадения номера новой отпайки с номером установленной, определяют знак управляющего сигнала (направление переключения РПН). Далее управляющие импульсы поступают в регистры блока контроля и управления РПН; соответствующие реле замыкаются – и начинается переключение. Устройство переходит в режим ожидания окончания переключения, контролируя соответствующие каналы блока контроля и управления РПН. После окончания переключения управляющие импульсы снимают, измеряют параметры объекта управления, проверяют соответствие их заданным ограничениям и снова сравнивают номера отпаек. Процесс повторяется, пока на регуляторе РПН не установится необходимая отпайка. Любые нарушения ограничений по параметрам (токи, напряжения), нарушения в работе устройства или регулирующего устройства в виде сообщений направляются в управляющую ЭВМ.

Оперативное управление режимами ЭС выполняют с помощью комплекса программ АЧП [3,8] и устройства АКУФ РУ. С целью адаптации законов управления и учета технических ограничений регулируемого трансформатора по уровням напряжений и коэффициентам трансформации вектор наблюдения уточняют путем измерения параметров режима (токов и напряжений) непосредственно на регулируемом трансформаторе. Такой подход позволяет повысить устойчивость управления к изменению внешних факторов и реализовать его автоматическим или автоматизированным способом в рамках существующей АСДУ [8].

Следовательно, в случае автоматического управления по закону (13), сначала выполняют проверку необходимости уточнения пассивных параметров ЭС. Если изменения зафиксированы, то осуществляют их обновление от центральной ЭВМ. Далее программой-драйвером генерируется запрос для АКУФ РУ на измерение местных параметров электрической сети, служащих для уточнения данных, полученных из базы данных оперативно-информационного комплекса ЭС. Используя указанную информацию, в соответствии с законом управления (13), определяют оптимальные значения коэффициента трансформации (14) и номер отпайки РУ, которую необходимо установить.

Применение АКУФ РУ позволяет ввести в систему управления нормальными режимами ЭС обратную связь, контролировать выполнение управляющих воздействий и оценивать эффективность управления как отдельными трансформаторами, так и энергосистемой в целом. Последнее дает возможность автоматизировать ряд функций оперативного управления и повысить эффективность использования РУ трансформаторов в задачах уменьшения потерь активной мощности в электрической системе.

Выводы

1. Электрические системы не являются оптимальными с учетом расхода электроэнергии при ее производстве, транспортировке и распределении. Одной из основных причин неоптимальности состояний ЭС является их неоднородность. В работе решена научная задача разработки метода определения обобщенного показателя неоднородности ЭС, содержащего дальние линии электропередачи. На основании приведенной математической модели неоднородности электрических сетей с учетом особенностей функционирования дальних линий электропередач показано, что для таких сетей из-за нестабильности продольных и поперечных параметров практически не может быть обеспечено их однородное состояние. Таким образом, обеспечение оптимальности их режимов требует применения соответствующих систем автоматического управления.
2. Для решения задачи определения законов оптимального управления РПН трансформаторов связи ЭС с учетом особенностей их влияния на процесс транспортировки и распределения электроэнергии в электросетях с дальними электропередачами была предложена математическая модель оптимальных э. д. с. небаланса, а также метод определения оптимальных коэффициентов трансформации РУ с учетом волновых свойств дальних ЛЭП, а также влияния несбалансированных коэффициентов трансформации трансформаторов связи и регулирования напряжений в центрах питания ЭС. Такое усовершенствование позволяет принимать более эффективные решения в задачах оптимального управления потоками мощности и напряжением в ЭС.
3. Применение устройства АКУФ РУ позволяет реализовать в автоматизированной системе оптимального управления нормальными режимами ЭС обратную связь по параметрам управления и обеспечивает возможность децентрализации отдельных задач оперативного управления таких, как адаптация параметров наблюдения, контроль за выполнением управляющих воздействий, оценки целесообразности управления отдельными трансформаторами и т. п. Последнее дает возможность повысить надежность и эффективность использования регулирующих устройств в ЭС.

Список литературы

1. Основні параметри енергозабезпечення національної економіки на період до 2020 року / [Стогній Б. С., Кириленко О. В., Праховник А. В., Денисюк С. П. та ін.]. – К.: Вид. Ін-ту електродинаміки НАН України, 2011. – 275 с. 2. Холмский В. Г. Оптимизация потокораспределения в замкнутых электрических сетях с высокой степенью неоднородности / В. Г. Холмский // Электричество. – 1965. – № 9. – С. 16 – 21.
3. Лежнюк П. Д. Моделирование компенсации влияния неоднородности электрических сетей на экономичность их режимов / П. Д. Лежнюк, В. В. Кулик, Д. І. Оболонський // Электричество. – 2007. – № 11. – С. 2 – 8.
4. Лежнюк П. Д. Оцінка взаємовпливу електричних мереж енергосистем з трансформаторними зв'язками / П. Д. Лежнюк, В. В. Кулик, О. Б. Бурикін // Технічна електродинаміка / Тематичний випуск: Проблеми сучасної електротехніки, ч. 7. – 2006. – С. 27 – 30.
5. Веников В. А. Дальние электропередачи переменного и постоянного тока / В. А. Веников, Ю. . Рыжов. – М.: Энергоатомиздат, 1985. – 272 с.
6. Комбіновані моделі нормальних режимів електричних систем з урахуванням особливостей довгих ліній електропередачі [Електронний ресурс] / В. В. Кулик, С. Я. Вишневський // Наукові праці ВНТУ. – 2012. – № 1.
7. Сулейманов В. М. Електричні мережі та системи / В. М. Сулейманов, Т. Л. Кацадзе. – К.: НТУУ «КПІ», 2008. – 456 с.
8. Лежнюк П. Д. Реалізація контролю і керування функціонуванням трансформаторів в електроенергетичних системах / П. Д. Лежнюк, К. І. Кравцов // Вісник Вінницького політехнічного інституту. – 2010. – № 6. – С. 84 – 86.