Аннотация
И.О. Лебедь, В.А. Панов Замена вычисления пространственной волны в приёмной камере газоструйного аппарата расчётом. Предлагается методика учёта пространственной волны в приёмной камере газоструйного аппарата, позволяющая применить теории распада произвольного разрыва для численного расчёта нестационарных граничных условий на стыке приёмной и рабочей камер. Интенсивность волны в приёмной камере находится из интегральных соотношений баланса массы и энергии. Получена формула изменения количества энергии в приёмной камере при нестационарном процессе.
При разработке математической модели нестационарного течения газа в проточной части газоструйного аппарата особое внимание уделяется заданию граничных условий. Одной из часто используемых для расчёта нестационарных граничных условий в пульсирующем газоструйном аппарате всё большее применение находит теория распада произвольного разрыва (РПР) [2], [3].
Суть этой теории заключается в следующем.
Если в некоторый начальный момент времени в потоке существует плоскость, на которой наблюдается разрыв функций параметров, то этот разрыв немедленно распадается на конфигурации устойчивых разрывов (ударная волна, волна разрежения и контактная поверхность) и зоны стационарного течения между ними. При этом автоматически удовлетворяется основные законы сохранения: массы, импульса и энергии.
Применение теории РПР для расчёта граничных условий на стыке двух одномерных состояний газа обычно не встречает затруднений. Однако расчёт РПР на границе одномерного течения в рабочей камере и трёхмерного течения в приёмной камере затруднён из–за пространственного характера волны в последней. Учитывая, что расчёт трёхмерного течения в приёмной камере нецелесообразен с точки зрения расчёта волновых процессов при одномерных течениях, важно разработать практически простой метод, который позволил бы на основе законов сохранения интегрально
учесть влияние волн в цилиндре. Так, в работе Рудого Б.П. [2] интенсивность пространственной волны находится из условия баланса энергии в проточной части на расчётном шаге.
Однако такое определение интенсивности волны страдает тем недостатком, что не учитывается изменение массы газа в возмущённой зоне. Кроме того, в данной методике излишне сложно определяется количество энергии, которым обмениваются приёмная и рабочая камеры в процессе нестационарного газообмена.
В настоящей работе предлагается метод учёта пространственной волны в приёмной камере на основе баланса энергии и массы газа в проточной части газоструйного аппарата.
Рассмотрим задачу о РПР при мгновенном попадании порции рабочего потока на стык камер (рис. 1).
По физике процесса давление в приёмной камере больше, чем в рабочей камере, поэтому конфигурация РПР включает в себя ударную волну и контактную поверхность, распространяющиеся в рабочей камере, и пространственную волну разрежения в приёмной камере.
Решить задачу о РПР – это значит, определить параметры потока в зонах 2 – 4 в зависимости от исходных параметров газа в зонах 5 и 1 и геометрии струйного аппарата. Методика расчёта конфигурации РПР подробно изложена в работе [3]. Расчёт ведётся в предположении, что течение в зонах 1 – 3 одномерное.
Основная трудность заключается в определении параметров газа в пространственной волне (зона 4).
Для определённости в начальный момент времени t газ в приёмной камере имел температуру и давление зоны 5. Через промежуток времени
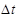волна распространилась по всему объёму приёмной камеры, и параметры газа за фронтом волны соответствуют параметрам зоны 4. Таким образом, зона 5 занимает весь объём приёмной камеры в момент t , а зона 4 – в момент 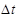. При этом величина расчётного шага 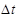связана с характерным размером приёмной камеры 
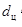и характерной скоростью распространения возмущений в ней 
соотношением:
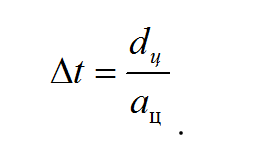
Изменение массы газа в приёмной камере за расчётный шаг составляет:
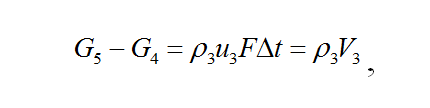
где
Определим изменение энергии газа в цилиндре за шаг.
Масса газа, занимавшая в начальный момент времени t объём приёмной камеры, расширилась и через 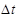заняла объём зоны 3. Работа расширения этой массы газа составляет 
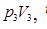, где 
– давление в зоне 3.
Полагая, что газ в приёмной камере в момент t покоился и её объём в течение расчётного шага не изменяется, тогда согласно первому закону термодинамики для адиабатного случая имеем:
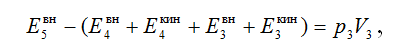
Это уравнение можно преобразовать так, что в одной части будет выражение, характеризующее уменьшение энергии газа в приёмной камере, а в другой – выражение для полной энтальпии газа в зоне 3:
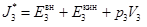
Тогда
Если предположить, что по завершении расчётного шага газ в приёмной камере успокоился, и его кинетическая энергия перешла в тепло, то уравнение баланса энергии (4) приобретает окончательный вид:
Уменьшение температуры и давления в зоне 4 обусловлено уменьшением в ней массы газа и энергии. Поэтому совместное решение уравнений баланса массы и энергии определит температуру и давление в зоне 4. При этом параметры газа в зоне 3 считаются известными из расчета РПР в первом приближении, проведенного при условии равенства параметров в зонах 4 и 5.
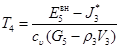
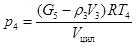
Таким образом, когда определены параметры в пространственной волне в цилиндре, можно рассчитать всю конфигурацию РПР и уточнить параметры вытекающего из цилиндра газа (зона 3).
Далее расчёт выпуска строится следующим образом.
Вычисляется объём цилиндра, соответствующий времени 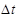, и с помощью метода объёмного баланса [1] определяется температура и давление газа в цилиндре к началу следующего шага. Затем происходит расчёт на следующем временном шаге.
Предложенная методика может быть использована в практических численных расчётах нестационарных граничных условий, обеспечивая выполнение законов сохранения без рассмотрения пространственной волновой картины в цилиндре.
Список использованной литературы
1. Глаголев Н. М. Рабочие процессы двигателей внутреннего сгорания. ГНТИ. М., 1950, 477 с.
2.Рудой Б. П. О законах сохранения при расчётах процессов наполнения и опорожнения рабочих объёмов двигателем со сгоранием 
.Труды УАИ, 1974, вып. 82, с. 3–11.
3. Рудой Б. П., Березин С. Р. Расчёт на ЭВМ газообмена ДВС. Учебное пособие, Уфа, 1979, 107 с.