Аннотация
А. Н. Козыряцкий, А. П. Кононенко, В. И. Мизерный На основании общей теории размерностей получены основные критерии подобия, необходимые для моделирования эрлифтов.
В гидравлике газожидкостных смесей, как и в ряде других наук, широкое применение имеет метод моделирования, когда исследуется не само явление или процесс, например, движущееся в газожидкостной смеси тело, поток водовоздушной смеси и т.д., а его модель обычно в уменьшенных размерах. Для возможности перенесения результатов эксперимента на модели в натуральный процесс необходимо, чтобы оба процесса были полностью подобны.
Различают три вида подобия, отличающихся степенью его полноты: геометрическое, кинематическое и динамическое. В настоящее время применение методов теории подобия к решению задач течения двухфазных потоков находится в стадии развития и поисков конкретных форм приложения.
Для упрощения зависимости и выявления главных параметров, определяющих движение в газожидкостной смеси, рассмотрим условия движения ее в трубе эрлифта. Для правильного моделирования эрлифта, а, следовательно, и расчета, крайне необходимо иметь кри- терии подобия. Несмотря на это, до сего времени нет достаточно обоснованных критериев подобия эрлифтов.
Как известно [ 1 ] полную определенность физического процесса, проходящего в трубе эрлифта можно считать установленной, когда известны следующие признаки явления: геометрические свойства системы; физические константы тел, образующих систем; начальное состояние системы; условия на внешних границах системы.
Предполагается протекание процессов в геометрически подобных системах.
Приняты следующие физические величины, влияющие на гидравлический режим потока водовоздушной смеси в трубе: средняя скорость водовоздушной смеси; плотности воды, воздуха и смеси, ускорения свободного падения; кинематическая вязкость воды, воздуха, смеси; время протекания процесса; удельные гидравлические потери; подача эрлифта; расход воздуха; диаметр, длина и шероховатость подъемной трубы.
Начальное состояние не влияет на движение водовоздушной смеси в трубе эрлифта в период нормальной его работы, а влияет лишь в период пуска. Условия на внешних границах определяется, в основном, давлением смесителя и на верхнем конце подъемной трубы эрлифта.
Итак, для построения модели эрлифтной установки, на которой могут быть поведены экспериментальные исследования, необходимо определить критерии подобия, составляющие основу моделирования. Их можно определить либо из условий тождественности уравнений, описывающих процессы, либо из анализа размерностей.
Найти указанные критерии непосредственно из уравнений физического процесса не представляется возможным. Это объясняется тем, что из–за сложности процесса в эрлифте практически невозможно получить дифференциальное уравнение движения газожидкостной смеси в трубе эрлифта, которое отвечало бы действительным процессам, происходящих в эрлифте.
Считая известными параметры, влияющие на исследуемый процесс, задачу по определению необходимых критериев подобия будем решать на основе теории размерностей.
Пусть исследуемый процесс в общем виде описывается уравнением
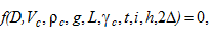
где D – диаметр подъемной трубы, м; Vc – средняя скорость водовоздушной смеси, м/с;
; g – ускорение свободного падения, м/с2;
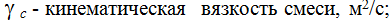; t – время, с; i – удельные гидравлические потери водовоздушного потока, Па/м; h – глубина погружения смесителя, м; 
трубы, м; H – высота подъема воды, м; 
– длина трубопровода, м;
Основные определяющие параметры, принятые в качестве независимых величин, находятся из условия неравенства нулю определителя матрицы, составленной из размерностей данных величин. В данном случае такие величины могут быть, например, D, Vc,
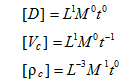
где L, M ,t – величины, принятые в системе СИ за основные [ L ] = м, [ M ] = кг, [t ] = сек.
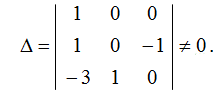
Запишем уравнение (3) в виде
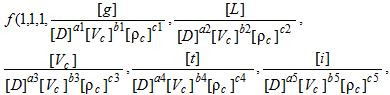
Определив показатели степеней при независимых переменных, найдем согласно второй П – теореме m–k критериев подобия. В нашем случае m = 10, k = 3
где m – число параметров, влияющих на исследуемый процесс и входящих в уравнение (1); k – число независимых величин, принятых за основные.
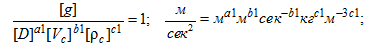
Аналогичным образом получаем остальные П – параметры, на основании которых критериальное уравнение процесса имеет вид
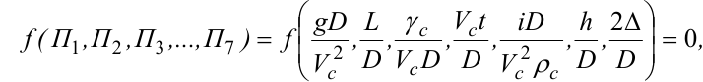
где Пi – безразмерный комплекс, критерий подобия.
Используя свойства П – параметров, умножим П2 на П5 находим критерий Эйлера
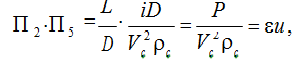
где P – потери на гидравлические сопротивление, Па;
Аналогично получаем
где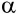 
– относительное погружение.
В результате критериальное уравнение (8) можно представить в виде
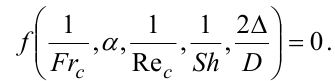
Согласно второй П – теореме, один из m–k найденных критериев является зависимым и при соблюдении остальных критериев выполняется автоматически. В нашем случае таким критерием будет u.
Для рассматриваемого случая при моделировании затруднительно принять П – теорему для установления качества критериев, обеспечивающих подобия. Но и в этом случае необходимо стремиться к постановке задачи в духе третьей теоремы подобия. Устанавливаем условие однозначности и критерии подобия путем логического анализа и контрольных экспериментов.
Окончательно с учетом критерия qn критериальное уравнение можно представить в виде
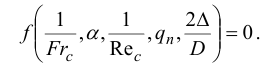
Согласно третьей П – теоремы, необходимым и достаточным условием подобия двух процессов ( модели и натуры ) является наличие пропорциональности между всеми сходственными параметрами, входящими в условия однозначности и равенство всех критериев подобия, т.е.
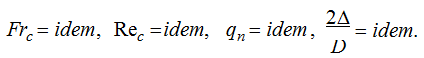
Добиться полного подобия процессов в модели и натуры нельзя, поэтому для выяснения возможности распространения результатов моделирования на натуру последние в дальнейшем сравниваются с исследованиями на натурных установках.
Список использованной литературы
1. Костанда В.С. Исследование и разработка эрлифтных и углесосноэрлифтных подъемов гидрошахт. Диссертационная работа на соискание ученой степени кандидата технических наук. Донецк, 1963.