Динамеческая модель фрезерования концевыми фрезами на станках с ЧПУ

Аннотация

В статье представлено динамические модели процесса резания при фрезеровании концевыми фрезами на станках с ЧПУ. Данные модели дают возможность использовать их во время моделирования процесса резания, для того чтобы исключить следы вибраций на обрабатываемых деталях.

Перед современным машиностроением стоит задача интенсификации технологических процессов с целью минимизации себестоимости изделия. При обработке деталей сложной пространственной формы нет альтернативы механической обработке – фрезерованием. Однако использование режимов резания, которые бы гарантировали высокую производительность обработки, ограничивается, в основном потерей динамической устойчивостью системы. Динамика процесса фрезерования является важным вопросом в повышении эффективности механической обработки.

Вибрации оказывают негативное воздействие на процесс резания, а именно: высокая шероховатость и низкая точность обработанной поверхности, чрезмерный шум в процессе резания, неравномерный износ режущего инструмента (режущих кромок), преждевременный выход из строя оснастки и оборудования [1].

Рис.1. Вибрации при фрезеровании

Во избежание вышеперечисленного практикой машиностроительного производства искусственно занижаются режимы резания, вследствие чего, увеличивается основное время обработки и повышается себестоимость детали, при этом конкурентоспособность продукции снижается в разы.

Таким образом, задача определения оптимальных режимов резания при фрезеровании сложных пространственных поверхностей является актуальной проблемой современного машиностроения.

Несмотря на обширные экспериментальные и теоретические исследования современные ученные и научные школы до сих пор не пришли к общему мнению по вопросу возникновения и развития автоколебаний при резании. Однако, все сходятся на том, что упругая система станок – приспособление – инструмент – деталь, а именно их жесткость и демпфирующие способности элементов технологической системы играют определяющую роль в динамике процесса резания.

Поскольку фрезерование сложных криволинейных 3-D поверхностей на станках с ЧПУ сопровождается неравномерностью распределения припуска на разных участках траектории с изменением в каждый момент времени объема срезаемого материала (MRR – Material Removal Rate), что приводит к изменению силы резания и ее составляющих, а движение инструмента выполняется по сложным траекториям формообразующих движений, то как следствие, возникают собственные затухающие колебания технологической системы.

Многие исследователи считают, что одной из основных причин возникновения самовозбуждающихся колебаний (автоколебания) в процессе резания являются динамические силы резания второго рода, связанные со срезанием следа с предыдущего оборота детали, являющиеся основным источником энергии, идущей на самовозбуждение и поддержание колебаний при резании «по следу» (впервые рассмотрено в [2]). В частности, они объяснили, что модуляция толщины срезаемого слоя, вызванная автоколебаниями, продуцирует колебательное поведение силы резания. Авторы предложили использовать теорию устойчивости дифференциально-разностных уравнений для исследования динамики вторичных колебаний. Исследование устойчивости дифференциальных уравнений с запаздывающим аргументом для анализа моделей фрезерования позволило получить уравнения для определения областей устойчивости, которые графически отображаются на диаграммах устойчивости. Такие диаграммы позволяют технологу подобрать корректные режимы обработки и обеспечить устойчивость резания.

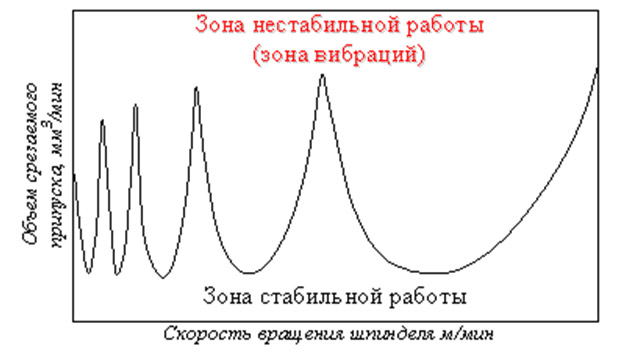
Рис.2. Пример диаграммы устойчивости режимов резания

Таким образом, для уменьшения влияния вибраций на обрабатываемую деталь необходимо управлять процессом фрезерования на станках с ЧПУ. При этом надо определить такой закон движения подачей формообразующего движения, который бы удовлетворял условие: наибольшее отклонение скорости снятия припуска вдоль обрабатываемой поверхности было минимальным. В результате квазистационарность процесса резания минимизируется и его можно отождествлять с обработкой поверхности постойной кривизны.

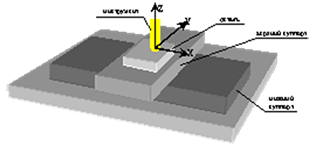
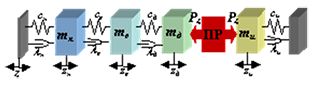
Анализ схемы формообразования при обработке сложных криволинейных поверхностей на станках с ЧПУ позволяет выделить основные динамические элементы упругой технологической системы и представить динамическую модель по каждой формообразующей координате, ограничившись четырьмя массами: нижний и верхний суппорта, деталь (приспособление) и инструмент [3]. По координате X масса m_в верхнего суппорта и m_д детали находятся под действием как кинематического, так и силового возбуждения, а массы m_н нижнего суппорта и m_и инструмента – под действием только силового возбуждения. По координате Y массыmв верхнего, m_н нижнего суппортов и m_д детали находятся под действием кинематического и силового возбуждения, а масса m_и инструмента – под действием силового возбуждения. По координате Z массы m_в верхнего, m_н нижнего суппортов и m_д детали находятся под действием кинематического и силового возбуждения, а масса m_и инструмента – под действием силового возбуждения.

а)	б)

Рис.3. Схема(а) и динамические модели 3-х координатного фрезерного станка с ЧПУ

Таким образом, математические модели упругой технологической системы, составленные в направлениях формообразующих координат, отличаются друг от друга. Математическая модель динамической системы в направлении координаты X:

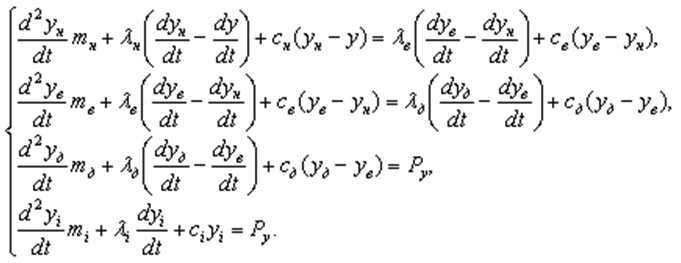
Динамическая погрешность формообразования по координате X:

Математическая модель динамической системы в направлении координаты Y:

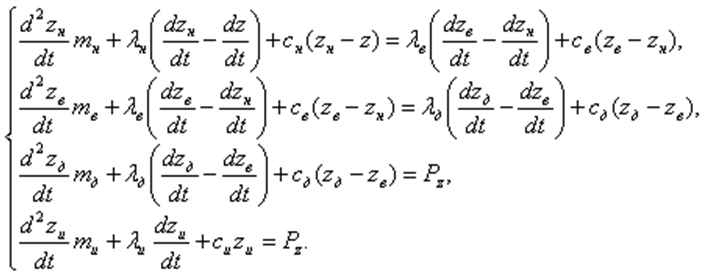
Динамическая погрешность формообразования по координате Y:

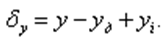
Математическая модель динамической системы в направлении координаты Z:

Динамическая погрешность формообразования по координате Z:

В математических моделях (10.24) и (10.26) приняты обозначения, которые соответствуют динамическим моделям (рис. 10.17, б, в), а именно: m – масса, c – жесткость, λ – коэффициент вязкого трения с соответствующими индексами. Учитывая значительные трудности при определении коэффициента вязкого трения, в дальнейших расчетах рекомендуется использовать коэффициент затухания колебаний ζ, связанный с λ зависимостью:

Список использованной литературы

1. F. W. Taylor, “On the art of cutting metals”, Transactions of the American Society of Mechanical Engineers, pp.31–35,1907.
2. Tobias S.A. The chatter of lathe tools under orthogonal cutting conditions / S.A. Tobias, W. Fishwick // Transactions of ASME. 1958. Vol. 80. Iss. 1. P. 1079–1088.
3. Петраков Ю.В. Автоматичне управління процесами обробки матеріалів різанням. –УкрНДІАТ, Київ, 2004.-384с.