
Автор: van Zyl J.E.
Университет Кейптауна, факультет гражданского строительства, Кейптаун, Южная Африка
Источник (англ.): van Zyl J.E. Theoretical Modeling of Pressure and Leakage in Water Distribution Systems / J.E. van Zyl // Procedia Engineering, Vol. 89, 2014, pp. 273-277
Перевод с англ.: Р.И. Горбунов
Цель этой статьи — обобщить последние теоретические разработки о соотношении давления и утечки в системах водоснабжения. Понятно, что высокие показатели утечек, часто встречающиеся в полевых исследованиях, в основном обусловлены областями утечки связанными с давлением в системе, которое приводит к упругой деформации. Кратко обсуждаются другие факторы, которые включают в себя гидравлические факторы утечек, гидравлику грунта и то, как отдельно распределенные утечки в зоне управления давлением, влияют на общий показатель утечек
Ключевые слова: давление, утечка, показатель утечки, количество утечек, водопроводная система, теория, модели
В последние годы произошли существенные изменения в понимании соотношения между давлением и утечкой на основе результатов теоретических, численных, экспериментальных и полевых исследований. В 2007 году van Zyl и Clayton [1] предложили четыре фактора, которые могут отвечать за наблюдаемую высокую чувствительность утечек к давлению, а именно: гидравлические факторы утечек, поведение материала трубы (изменение площади зоны утечки в зависимости от давления), гидравлика грунта и потребление воды. Впоследствии был добавлен пятый фактор — то, как отдельно распределенные утечки в зоне управления давлением, влияют на общий показатель утечек [2].
Цель этой статьи — обобщить теорию воздействия давления на утечки для каждого из вышеприведенных факторов. Влияние потребления воды не исследуется, поскольку оно не является прямым составляющим утечек.
Утечка может рассматриваться с точки зрения отверстия в трубе распределительной системы. Гидравлисеская сеть с отверстиями достаточно изучена, зависимость скорости потока воды Q через отверстие от площади отверстия A и давления h в трубопроводе описывается уравнением:

где Cd — коэффициент разряда, учитывающий потери энергии и сжатие струи, а g — ускорение свободного падения.
Однако, в теории утечек используется более общая форма уравнения для описания взаимосвязи между давлением и утечками [3]:

uде Q — расход утечки, C — коэффициент утечки, h — среднее давление на участке(СДУ) и N1 — показатель утечки. В то время как уравнение отверстия (1) предсказывает, что показатель утечки составляет 0,5, в исследования на местах дают значения до 2,9, хотя подавляющее большинство показателей утечки составляет от 0,5 до 1,5
В то время как расчетная величина показателя утечки воды через отверстие в трубопроводе должна составлять 0,5 для отверстия с фиксированной площадью, это справедливо только для турбулентного потока. Для ламинарного потока соотношение между скоростью потока и давлением становится линейным, и, следовательно, ламинарный поток может объяснить величину показателя утечки — 1. Режим потока определяется числом Рейнольдса (Re), и поток через отверстия обычно является ламинарным при Re ниже 10 и турбулентным при Re выше 4000–5000 [5].
При фиксированном числе Рейнольдса максимальная скорость, при которой поток струи будет ламинарным или переходным, определяется функцией периметра отверстия и, в меньшей степени, вязкости воды, которая в основном зависит от температуры [1].
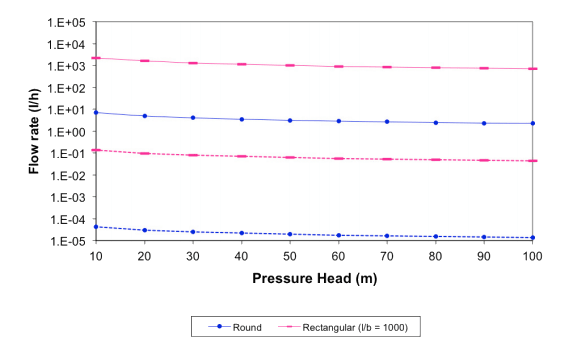
Рисунок 1 — Максимальный ламинарный (пунктирная линия) и переходный (сплошнай линия) поток для круглых отверстий и трещин с отношением длины к ширине 1000
На рисунке 1 показаны максимальные значения ламинарных и переходный потоков, возможные для круглого отверстия и трещины с отношением длины к ширине 1000. Под давлением 50 м, трещина способна обеспечить максимальную пропускную скорость для ламинарного 0,06 л/ч и переходного 1000 л/ч потоков.
Основываясь на полученных результатах, маловероятно, что значительная часть утечки в распределительной системе может быть ламинарного типа. Переходный поток может быть намного больше, но чем больше скорость потока, тем ближе эффективный показатель утечки будет стремиться к значению 0,5 на границе переходного потока. Таким образом, также маловероятно, что переходный поток будет иметь большое влияние на показатель утечки системы.
May[6] в 1994 году представил концепцию FAVAD (Fixed and Variable Area Discharges) — жесткой и изменяющейся площади выходного отверстия, предположив, что некоторые отверстия неизменны, в то время как другие будут расширяться с увеличением давления. Он предположил, что площадь утечки изменяется линейно с давлением, и это было позже подтверждено Cassa и др. [7] в исследовании на конечных элементах поведения отверстий и трещин в различных материалах труб (uPVC (непластифицированный поливинилхлорид), чугун, сталь и асбестоцемент) в двых состояниях нагрузки. Это исследование показало, что в условиях упругости области утечек изменяются линейно с давлением, и поэтому отношение площади отверстия может быть описано начальной площадью A0 и коэффициентом отклонения в виде:

Коэффициент отклонения поверхности отверстия зависит от свойств утечки, а также от свойств материала и сечения трубы. Для круглых отверстий m очень мало, а для продольных, спиральных и круговых трещин были предложены формулы для m на основе исследований CFD [8]. Предположение о упругой деформации, присущей уравнению 3 считается разумным для общего анализа, хотя известно, что утечки в пластиковой трубе также подвержены гистерезису и пластической деформации [9].
Подставляя уравнение 3 в уравнение 1, получим уравнение FAVAD:

Van Zyl и Cassa [10] определили безразмерное число утечек LN, как отношение между расширяющимися и фиксированными порывами в уравнении 4, как:
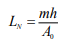
Они обнаружили взаимно однозначное соотношение между порядком утечки и показателем утечки, как показано на рисунке 2, которое описываются следующим уравнением:

Это соотношение в сочетании с уравнениями для прогнозирования деформации поверхности отверстия (см. [8]) может быть использовано для прогнозирования деформации отдельных участков и прогнозирования изменений показателя утечек при разных давлениях.

Рисунок 2 — Связь между порядком и показателем утечки.
Гидравлика почвы характеризуется линейной зависимостью между давлением и утечкой, как описано законом Дарси. Однако почвы, как правило, не способны обрабатывать высокие потоки энергии
водяных струй от утечек в водораспределительных трубах, и поток не описывающийся законом Дарси, вероятно, будет близок к утечкам, возможно, в виде гидравлического разрыва.
В экспериментальных исследованиях, основанных на идеализированной почве, наблюдалась подвешенная зона
взаимодействия утечек с почвой, и есть признаки того, что подвешенная зона
действует как механизм рассеивания энергии [11].
В то время как почвы, прилегающие к месту утечки, могут иметь некоторое влияние на соотношение давления и утечки, маловероятно, чтобы какая-либо почва могла содержать давление, которое обычно встречается в системах водоснабжения, и, таким образом, воздействие почв на реакцию давления утечка, вероятно, будет невысоким.
Для результирующих последствий множества утечек Schwaller и van Zyl [2] показали, что модель FAVAD также может использоваться для описания поведения участков контроля давления с множеством утечек и что параметры модели FAVAD существенно связаны с итоговым количеством всех отдельных отверстий и отклонений их поверхности.
В этой статье собрана основная теория факторов, влияющих на соотношение давления и утечек в системах водораспределения. Поведение материала труб (т.е. расширение зон утечки с увеличением давления) является основным фактором, определяющим высокие показатели утечек, наблюдаемые в исследованиях на местах. Однако на показатель утечки также могут влиять гидравлические факторы утечек, гидравлика почвы, потребление воды и суммарный результат множества утечек на участках изменения и контроля давления.
1. J.E. Van Zyl, C.R.I. Clayton, The effect of pressure on leakage in water distribution systems. Water management, 160 (20149 109-114
2. J. Schwaller, J.E. van Zyl, Implications of the Known Pressure-response of Individual Leaks for Whole Distribution Systems. Procedia Engineering, 70 (2014) 1513-1517
3. A. Lambert, T. Brown, M. Takizawa, D. Weimer, A review of performance indicators for real losses from water supply systems. Aqua, 48 (1999) 227-237
4. M. Farley, S. Trow, Losses in Water Distribution Networks, IWA Publishing, London, 2003
5. I. Idelchick. Handbook of Hydraulic Resistance, Begell House, 1994.
6. J. May. Pressure dependent leakage. World Water and Environmental Engineering, 1994.
7. A.M. Cassa, J.E. van Zyl, R. Laubscher, A numerical investigation into the effect of pressure on holes and cracks in water supply pipes. Urban Water Journal, 7 (2010)109-120
8. A.M. Cassa, J.E. van Zyl, Predicting the pressure-leakage slope of cracks in pipes subject to elastic deformations. Journal of Water Supply: Research and Technology — AQUA, 62 (2013) 214-223.
9. M. Ferrante, C. Massari, B. Brunone, S. Meniconi, Experimental Evidence of Hysteresis in the Head-Discharge Relationship for a Leak in a Polyethylene Pipe, Journal of Hydraulic Engineering, 137 (2011) 775-780.
10. J.E. van Zyl, A.M. Cassa, Modeling Elastically Deforming Leaks in Water Distribution Pipes, Journal of Hydraulic Engineering, 140 (2014) 182-189.
11. J.E. van Zyl, M.O.A. Alsaydalani, C.R.I. Clayton, T. Bird, A. Dennis, Soil fluidisation outside leaks in water distribution pipes — preliminary observations. Proceedings of the Institution of Civil Engineers: Water Management, 166 (2013) 546–555.