
Рис. 1 – Схематичное изображение ректификационной колонны
Авторы: M. Sharmila, Ms. V. Mangaiyarkarasi
Автор перевода: Пасько Е. С.
Источник (англ.): Modeling and Control of Binary Distillation Column
Ректификация – непрерывный процесс, широко применяющийся в нефтяной и химической промышленностях. Значительная часть энергии, использующейся в этих отраслях, идет на поддержание этого процесса, т.к. между тарелками колонны происходит обмен большим количеством тепла. Из этого следует, что чтобы процесс был эффективным с энергетической точки зрения, необходимо заняться его проектированием и управлением, чтобы получить конечные и промежуточные продукты желаемого качества и чтобы процесс в целом был более экономичным.
В настоящей работе для разработки математической модели ректификационной колонны и системы управления составом выходного пара было использовано графическое программирование в среде LabVIEW. Результаты моделирования можно применить в качестве данных первого приближения для разработки колонн или технико-экономического обоснования проектов.
Ректификационная колонна играет важную роль в газо- и нефтехимической промышленности. Ректификация – это процесс, в течение которого жидкая или газообразная смесь двух или более веществ разделяется на фракции желаемой концентрации с помощью подвода или отвода тепла. Бинарная ректификационная колонна используется для разделения двух компонентов. Примером бинарной смеси может служить смесь метанола и воды. На рис. 1 схематично изображена ректификационная колонна. Обычно в состав колонны входит несколько тарелок – тарельчатые колонны являются наиболее эффективными. Ректификационная колонна состоит из нескольки тарелок, конденсатора (дефлегматора), кипятильника (дистилляционного куба) и вертикальной колонны, внутри которой и происходит разделение. В этой работе ректификация рассматривается как непрерывный процесс. Это означает, что исходный продукт подается непрерывно. Здесь исходное вещество является входным воздействием для колонны. Колонна разделяется на две части – на отпарную секцию и секцию ректификации. Тарелки, расположенные выше тарелки питания, называются отпарной секцией.
Питающая бинарная смесь подается на тарелку питания с раходом Ff и молярной долей компотента А Cf. Отбираемый с верха колонны пар полностью конденсируется в дефлегматоре и стекает в ёмкость сбора оросительной фракции. Часть жидкости из этой ёмкости подается орошением обратно на верхнюю тарелку колонны с расходом FR, и часть удаляется из ёмкости в качестве результирующего выходного продукта с расходом FD. Примем, что количество жидкости, оставшееся в ёмкости орошения, равно MRD, и молярная доля компонента А в ней равна XD. Расход жидкости, выходящей из низа колонны, равен FB, а концентрация компонента А – XB. Часть этой жидкости, называемой кубовым остатком, подогревается в кипятильнике и подается обратно в колонну с расходом v. Пусть количество жидкости, находящейся в кипятильнике, равно MB. Колонна содержит N тарелок, которые пронумерованы снизу вверх.

Рис. 1 – Схематичное изображение ректификационной колонны
Ректификационная колонна, как было сказано выше, состоит из нескольких компонентов, в которых протекают массо- и энергообменные процессы, которые можно приближенно описать нижеследующими тезисами:

Принимая во внимание вышеперечисленные допущения, уравнения, описывающие систему, могут быть выписаны в следующем виде:
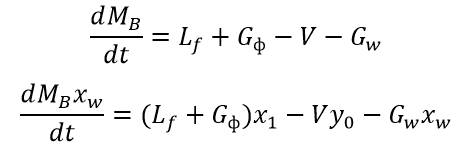
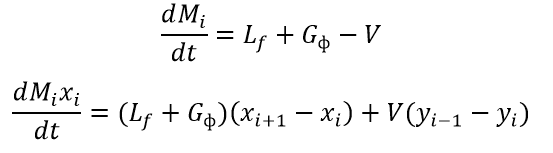

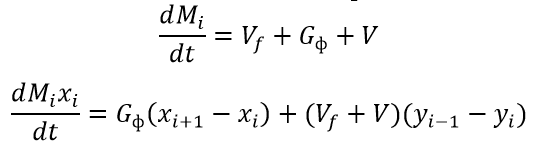

На основе вышеприведенных равенств была разработана модель ректификационной колонны в LabVIEW. Выходными, т.е. управляемыми, величинами являются концентрации дистиллята и кубового остатка, а управляющими воздействиями являются расход орошения (L) и расход пара (V).
Контроллер генерирует управляющий сигнал, основываясь на выбранном законе управления и на значении входной переменной. Входной переменной для контроллера служит ошибка рассогласования, т.е. разница между заданным входом и выходом. Чтобы достичь желаемого качества выходных продуктов, в данной работе был выбран закон управления по обратной связи – П, ПИ, ПИД.
Ниже перечислены различные подсистемы колонны и схемы их моделирования:
Подсистема i-той тарелки имеет два входа – xi+1 и xi-1 (концентрации жидких фаз соседних тарелок), и один выход – xi (концентрация жидкости на i-той тарелке). Также с помощью уравнения парожидкостного баланса вычисляется yi – концентрация газовой фазы. На рис. 4.1 показана схема моделирования i-той тарелки.

Рис. 4.1 – Схема моделирования i-той тарелки
Подсистема тарелки питания имеет 4 входа – xi+1, xi-1, xf, zf (концентрации жидкостей соседних тарелок и питающей смеси и концентрация газовой фазы питания) и один выход. На рис. 4.2. показана схема моделирования.
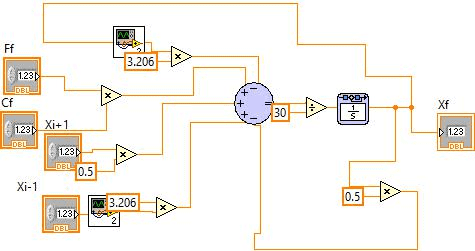
Рис. 4.2 – Схема моделирования тарелки питания
Уравнение для конденсатора и флегмовой ёмкости не является итеративным. Схема моделирования приведена на рис. 4.3.
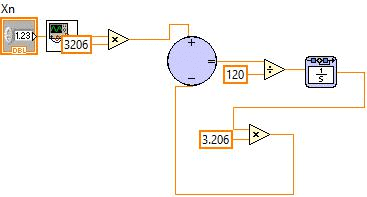
Рис. 4.3 – Схема моделирования конденсатора и флегмовой емкости
Модель колонны была линеаризована в окрестности точки [99.25%, .10%], т.е. концентрации дистиллята и кубового остатка. На вход системы было подано шаговое изменение концентрации в 5%, после чего было проанализированы изменения уровня концентраций дистиллята и кубового остатка. Чтобы пронаблюдать изменения концентраций выходных продуктов, были использованы различные значения коэффициентов ПИД-регулятора Kp, TI, TD. Результаты наблюдений приведены на рис. 5.1-5.3.
1 вариант: Пропорциональный регулятор:
KP1 = 49.095,KP2 = 32.183

Рис. 5.1 – Изменение концентрации дистиллята во времени (П-регулятор)
2 вариант: Пропорционально-интегральный регулятор:
KP1 = 24.7486 Ti 1 = 9.24609,KP2 = 28.1027 Ti 2 = 7.3494

Рис. 5.2 – Изменение концентрации дистиллята во времени (ПИ-регулятор)
3 вариант: Пропорционально-интегрально-дифференциальный регулятор:
KP1 = 15.3594 Ti 1 = 6.54891 Td 1 = .1891

Рис. 5.3 – Изменение концентрации дистиллята во времени (ПИД-регулятор)
Вариант I: В случае выбора П-закона наблюдается значительная статическая ошибка, так что такой регулятор является неприемлемым.
Вариант II: В случае выбора ПИ-регулятора статическая ошибка исчезает из-за ввода интегральной составляющей, однако длительность переходного процесса и перерегулирование слишком велики, так что ПИ-регулятор с заявленными коэффициентами также является неприемлемым.
Вариант III: В случае выбора ПИД-закона с хорошо подобранными коэффициентами с помощью интегральной составляющей была устранена статическая ошибка, а дифференциальная составляющая ускорила переходный процесс и уменьшила перерегулирование. Переходная характеристика является менее колебательной. Подобный регулятор можно счесть приемлемым.
В ходе работы была разработана математическая модель ректификационной колонны, основанная на уравнениях энергетического баланса. После сравнения результатов моделирования системы с различными регуляторами наиболее приемлемым оказался регулятор с ПИД-законом управления, т.к. при его применении статическая ошибка устраняется интегральной составляющей, а длительность переходного процесса уменьшается дифференциальной составляющей. Таким образом, ПИД-регулятор является наиболее предпочтительным способом получить выходной продукт желаемого качества.