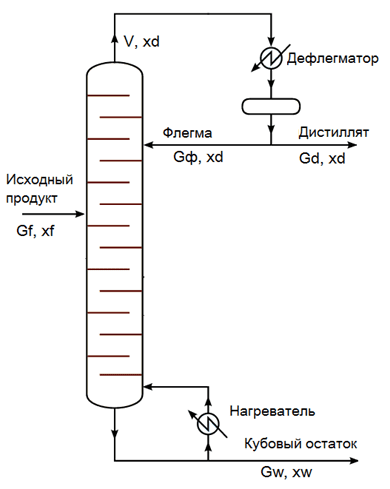
Рисунок 1 – Вид колонны и изображение основных переменных процесса
Авторы: Пасько Е. С., студент, Жукова Н. В., доц., к.т.н
Источник: Автоматизация технологических объектов и процессов. Поиск молодых
/ Сборник научных работ ХV научно-технической конференции аспирантов и студентов в г. Донецке 26-27 мая 2016 г. – Донецк, ДонНТУ, 2016. – 330 с.
Ректификация с помощью ректификационных колонн – эффективный и широко применяющийся метод разделения жидких смесей, состоящих из двух или большего количества компонентов с разными температурами кипения. В данной работе рассматривается случай разделения смеси на две фракции. Общий вид подобной колонны показан на рис. 1. Gf, xf – расход и концентрация исходной смеси, xd, xw – концентрации дистиллята и кубового остатка соответственно, V – расход пара, выходящий из верха колонны, Gd, Gф, Gw – расходы дистиллята, флегмы и кубового остатка соответственно[1].

Рисунок 1 – Вид колонны и изображение основных переменных процесса
Показателем эффективности технологического процесса принимается концентрация легкокипящей фракции в дистилляте, состав же кубового остатка может меняться в произвольных пределах. Возмущающими воздействиями являются расход исходной смеси и ее состав. Управляющие воздействия – расход флегмы (рефлюкса), подаваемой в колонну орошением и расход пара, подаваемого в кипятильник[2].
Представив объект в виде «черного ящика», можно получить следующую схему анализа технологического процесса ректификации с точки зрения основных материальных потоков и их информационных переменных (рис. 2).
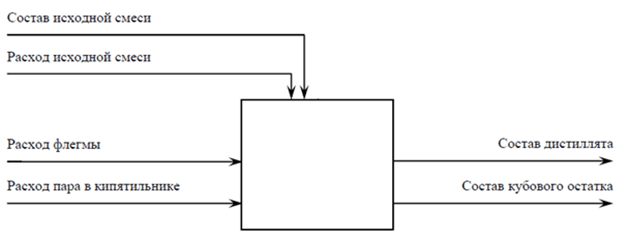
Рисунок 2 – Схема анализа ТП ректификации с точки зрения основных информационных потоков
Ректификационная колонна является сложным объектом со значительным запаздыванием[3-5]. Так как время между подачей воздействия и реакцией объекта относительно велико, необходимо применить вычислительное устройство, которое, используя математическую модель объекта, будет определять значения управляющих воздействий, обеспечивающие требуемое значение выходной величины.
Чтобы промоделировать массообменные процессы в колонне, можно исследовать происходящее на каждой тарелке колонны. Распределение параметров процесса по тарелкам изображено на рис. 3. N – количество тарелок, f – номер тарелки питания, Vi – поток пара через i-тую тарелку, Li – поток жидкости, стекающей через i-тую тарелку, xi и yi – содержания низкокипящей фракции в жидкой и паровой фазе соответственно.
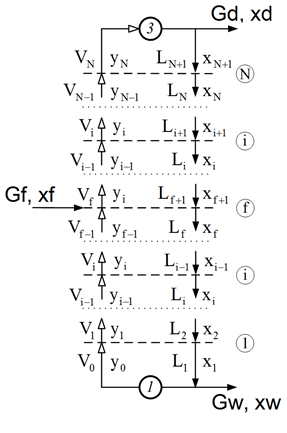
Рисунок 3 – Распределение параметров процесса по тарелкам колонны
Основные уравнения материального баланса в колонне:

Для построения математической модели примем следующие допущения:
С учетом вышеизложенных допущений уравнения, описывающие работу колонны, приведены в следующих формулах (M – количество вещества на i-той тарелке, кмоль)[3].
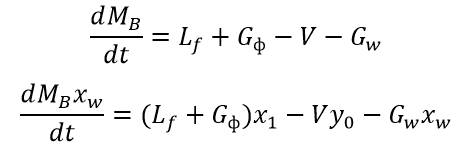
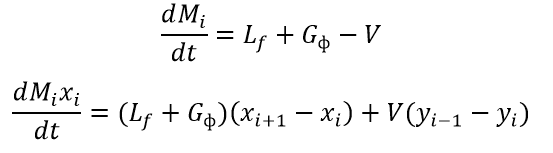

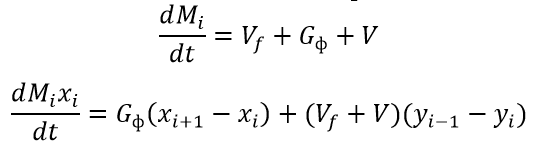

Систему автоматизации следует строить таким образом, чтобы обеспечивалась компенсация возмущений, таких как колебания расхода исходной смеси. Имеет смысл применение регулятора соотношения расходов, который бы заранее корректировал подачу флегмы в колонну в ответ на изменение расхода исходной смеси. Возможная реализация подобной системы изображена на рис. 4.
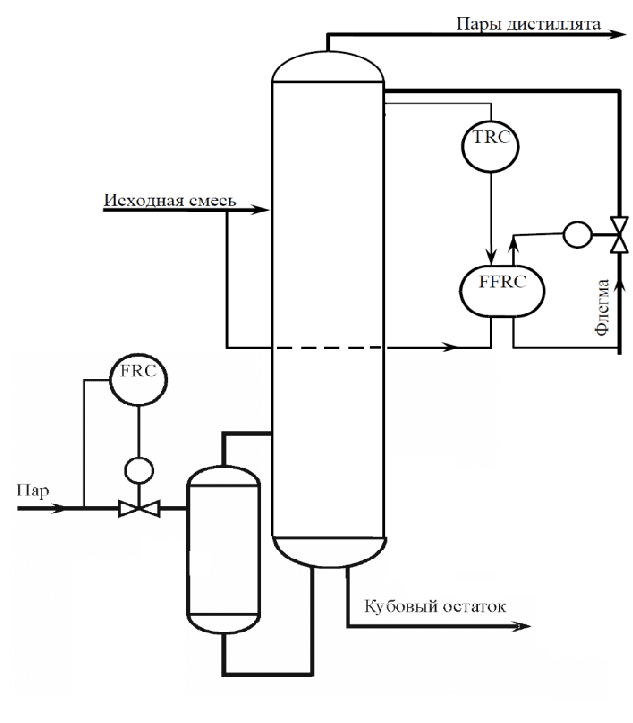
Рисунок 4 – Схема автоматизации колонны с использованием регулятора соотношения расходов
На рисунке показана двухконтурная система регулирования температуры. При увеличении подачи в колонну исходной смеси регулятор увеличивает подачу флегмы, и наоборот. Само же соотношение расходов определяется регулятором температуры.
Изменение расхода пара, подаваемого в колонну, оказывает относительно малое влияние на состав дистиллята, так что для регулирования подачи пара достаточно простой одноконтурной системы с обратной связью.
Исходя из вышесказанного, формула, описывающая расход флегмы в колонну, имеет вид:
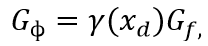
где γ(xd) – требуемое соотношение расходов, определяемое регулятором температуры.
Из вышеприведенных формул получим:

где V – суммарный поток пара, выходящий из верха колонны.
Это уравнение можно считать основным для последующего расчета зависимостей концентрации дистиллята. Таким образом, задача состоит в разработке конкретной численной зависимости gamma(xd).