Моделирование переходных процессов в асинхронных двигателях тяговых электромеханических комплексов двоосных электровозов

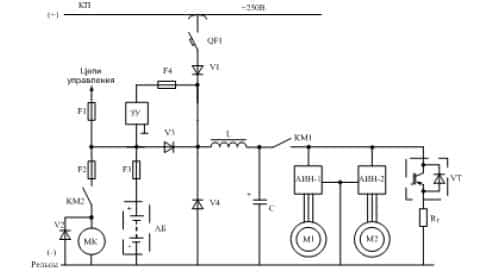
Рисунок 1 – Упрощенная электрическая схема двухосного рудничного контактно–аккумуляторного электровоза с тяговым асинхронным двигателем где: QF1 – вводной автоматический выключатель; V1 – заградительный диод; ЗУ – зарядное устройство; АБ – аккумуляторная батарея; КМ1, КМ2 – линейные контакторы; L, C – соответственно дроссель и конденсатор фильтра; АИН1, АИН2 – автономные инверторы; V3 – шунтирующий диод; V4 – запирающий диод; VT, Rт – соответственно тормозной чоппер и тормозной резистор; М1, М2 – тяговые асинхронные двигатели; МК – электрический двигатель компрессора; V2 – шунтирующий диод электрического двигателя компрессора; F1, F2, F3, F4 – предохранители

В силу изложенного, естественно, что эффективность функционирования тягового комплекса в целом будет определяться синхронностью работы каждого из двух его слагаемых модулей, в т.ч. близостью или идентичностью его электрических параметров и, прежде всего, тяговых электрических двигателей. Разница электрических параметров тягових модулей электровоза может быть также следствием буксования или юза одной из двух колесных пар. К сожалению, рекомендуемая разница до 2% разброса этих показателей ТЭД на практике является редким исключением. Как показали исследования [5], на практике разница электрических параметров ТЭД рудничных электровозов лежит в пределах 7 – 18%. Безусловно, такой разброс приводит к разности частот вращения ТЭД с вытекающими отсюда последствиями перегрузки одного и недогрузки другого двигателя по току, т.е., очевидно, что для требуемого уровня функционирования тягового комплекса двоосного электровоза, необходим постоянный мониторинг состояния текущих электрических параметров тяговых двигателей и адекватная реакция со стороны СУ ТЭП по минимизации образовавшейся разницы.

Реальным вариантом решения этой проблемы будет создание и реализация СУ соответствующего алгоритма управления. Последний, в свою очередь, не может быть реализован без предварительных исследований реальных режимов поведения тягового комплекса, т.е. моделирования этого процесса. Прежде всего, это относится к моделированию процессов в ТАД.

Изложение материала и результаты. В течение цикла технологического функционирования в подземных выработках железорудных шахт электровоз превращается в чрезвычайно сложный динамический объект, который с большим трудом поддается математическому описанию, то есть математическому моделированию. Меж тем, задание авторов – это получение для исследований модель, которая позволит проверить изменения процессов в ТАД с минимально возможными погрешностями.

Точность определения параметров ТАД в настоящее время достигается, как правило, применением известных методов оптимизации: множителей Лагранжа, вариационного исчисления, динамического программирования, принципа максимума, линейного программирования, симплексного метода, нелинейного программирования, геометрического программирования, метода наименьших квадратов, оптимальных наблюдателей [7]. Недостатком перечисленных методов является необходимость применения функциональных зависимостей, которые должны быть заранее известны. Выполнение большого числа математических действий при реализации перечисленных ранее методов – решении системы линейных или дифференциальных уравнений высокого порядка повышает требования к функциональным возможностям микропроцессорной вычислительной системы и усложнению программного обеспечения.

Для практической реализации системы идентификации и диагностики электрических параметров ТАД в реальном времени – слагаемых двухмодульных тяговых электромеханических систем рудничных электровозов целесообразна разработка методов с использованием нахождения минимального числа параметров по измеренным данным и оптимизацией их значений легко алгоритмически реализуемыми простыми способами, например, методом дихотомии.

С этой целью авторами разработан метод, который заключается в сравнении переходных процессов, полученных по измеренным координатам и рассчитанных на достаточно простой математической модели для условий рабочих режимов работы тягового электропривода электровоза [7].

Непрерывная математическая модель ТАД представляет собой многосвязанную систему, которая содержит внутренние нелинейные обратные связи. Поэтому при синтезе с целью упрощения непрерывной системы используется математическая модель ТАД во вращающейся системе координат.

Для синтеза автоматических регуляторов и анализа динамических режимов замкнутых ТЭМК с асинхронными двигателями, синтезированными для векторного управления, используются двухфазные математические модели, которые адекватно отображают процессы, которые протекают в реальной машине [7].

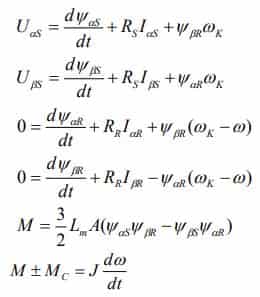
где R_S , R_R – активные, приведенные к статору сопротивления статора и ротора; L_S , L_R – активные, приведенные к статору сопротивления статора и ротора; L_m – главная магнитная взаимная индуктивность статора и ротора;

Дифференциальным уравнениям и уравнениям связей соответствует структурная схема ТЭМК с ориентацией по току и потокосцеплению статора приведенная на рис. 2. Структура представляет собой нелинейную многосвязанную систему.

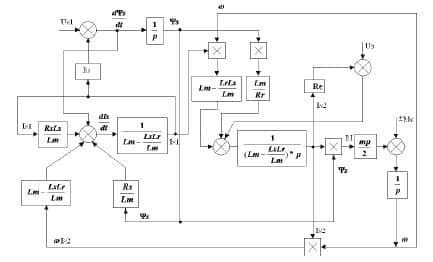
Рисунок 2 – Структурная схема тягового асинхронного двигателя с ориентацией по току статора

Уравнения возбуждения статора постоянным напряжением U_п

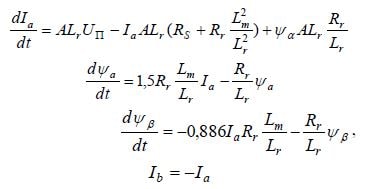
Решение системы дифференциальных уравнений позволяет получить информацию о токе и потокосцеплении статора в переходном процессе при двухфазном возбуждении постоянным током ТАД представлен на (рис. 3).

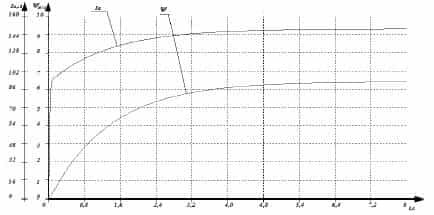
Рисунок 3 – Графики переходных процессов по току статора и потокосцеплению тягового асинхронного двигателя

Выводы и направление дальнейших исследований. По результатам исследования можна сделать следующие выводы:

Разработанная математическая модель тягового асинхронного двигателя в комплексе тягового электромеханического комплекса – тягового электропривода по мгновенным и средним значениям, описываемая рекуррентными соотношениями позволяет рассчитать мгновенные и средние значения координат, соответствующие координатам, измеренным датчиками СУ ТАП.

Применение математической модели предлагаемой структуры и создание системы по средним значениям текущих электротехнических параметров тяговых асинхронных двигателей позволит избавиться от помех, влияющих на точность исследований, и повысить адекватность результата вычислений, а значит построить адекватный алгоритм работы СУ ТЭМК.

Перечень ссылок

1. Дебелый В.Л. Основные направления развития шахтного локомотивного транспорта / В.Л. Дебелый, Л.Л. Дебелый, С.А Мельников // Уголь Украины. – 2006. – №6. – С.30–31.
2. Синчук О.Н. Перспективы развития шахтных (рудничных) электровозов с энергосберегающими видами тяговых электроприводов / О.Н. Синчук, С.В. Лебедкин, И.О. Синчук, О.О. Удовенко, О.В. Пасько // Вісник Східноукраїнського національного університету імені Володимира Даля. – Луганськ: СНУ ім. В. Даля. – 2006. – № 8 (102). – С. 83–92
3. Синчук О.Н., Устенко А.В., Сменова Л.В. Тяговый электромеханический комплекс шахтного двуосного электровоза с микропроцессорной системой диагностирования. Международный информационный научнотехнический журнал Локомотив–информ – № 07 (85), 2013.
4. Кордаков В.Н., Анискин Б.Г., Лакота О.Б., Коржев А.А. Электровозный транспорт на горных предприятиях: Проблемы и их решения, Горные машины и автоматика, вып. 5, М.:Издательство Новые технологии,2003,с.13– 15.
5. Пасько О.В. Комбинаторика схем тягового электропривода переменного тока. //Вестник национального технического университета Харьковский политехнический институт. Серия Электротехника, электроника и электропривод. Выпуск 43.–Харьков.НТУ ХПИ.–2004.с.121–125.
6. Bertil Oderg. Computer–controlled ore transportation at the LKAB mane inRurina–Sweden Information of ASEA.1997/–212p.
7. Lane Whale. New haulage level at Kurina, Sweden, has massive capacity. – Mining Journal, Jule, 1985.– vol.№6– 122p.