Разделение трафика в сетях MPLS – иерархический подход с несколькими критериями
Авторы: Jose M. F. Craveirinha, Joao C. N. Climaco, Marta M. B. Pascoal, Lucia M. R. A. Martins
Автор перевода: В. А. Жильцов
Источник: Journal of Telecommunications and Information Technology, 4, 3-10. http://www.researchgate.net/...
Аннотация – В данной работе рассматривается новая иерархическая многокритериальная модель маршрутизации, связанная с двухпутным методом разделения трафика в сетях MPLS, при котором пропускная способность, требуемая данным потоком трафика от узла к узлу, делится на два непересекающихся пути. Модель имеет два уровня целевых функций и ряд ограничений. Представлен алгоритмический подход к расчету недоминируемых решений и выбору оптимальных компромиссных решений этой задачи. Также представлен ряд вычислительных экспериментов.
Ключевые слова – многокритериальная оптимизация, многокритериальные наикратчайшие пути, маршрутизация телекоммуникационных сетей, Интернет/MPLS.
1. Введение
Проблемы маршрутизации в современных мультисервисных сетях связи включают в себя расчет путей, удовлетворяющих различным техническим ограничениям (обычно связанным с качеством обслуживания (QoS)) и стремящихся одновременно оптимизировать
соответствующие метрики. Множественность метрик QoS и функций стоимости, которые могут быть вовлечены в модели, и потенциальные конфликты между такими метриками / функциями делают, что существуют потенциальные преимущества в развитии моделей многокритериальной маршрутизации в этой области, которые зависят от особенностей функциональных возможностей сети и принятой структуры маршрутизации. Обзор применения инструментов многокритериального анализа решений (MCDA) к важным проблемам планирования и согласования телекоммуникационных сетей можно увидеть в [7]. В работе [1] представлен обзор современного состояния приложений MCDA для планирования телекоммуникационных сетей и решения проблем, в том числе раздел, посвященный моделям маршрутизации, а в [2] – обзор и тематическое исследование моделей многокритериальной маршрутизации в телекоммуникационных сетях.
В частности, платформа многопротокольной коммутации по меткам (MPLS) для IP-сетей позволяет реализовать расширенные схемы маршрутизации, а именно явные маршруты, удовлетворяющие требованиям QoS, и подготовлена для работы с многопутевой маршрутизацией, включая разделение трафика. MPLS является недавней мультисервисной интернет-технологией, основанной на передаче пакетов с помощью определенного метода коммутации меток пакетов. Среди других усовершенствованных механизмов маршрутизации использование явных маршрутов характеризуется тем, что путь, обозначенный как путь коммутации меток (LSP), за которым следует каждый поток пакетов от узла к узлу определенного типа, полностью определяется входящим маршрутизатором (соответствующим исходящему узлу). Эта технологическая платформа готова иметь дело с многопутевой маршрутизацией, используя понятие разделения трафика, которое состоит из разделения потока пакетов каждого потока, вдоль двух или более непересекающихся путей так, чтобы сумма полос пропускания, доступных в тех путях, удовлетворяла требованию пропускной способности каждого типа потока, в зависимости от класса обслуживания.
В этой работе мы рассматриваем новую иерархическую модель многокритериальной маршрутизации, связанную с методом двухпутной маршрутизации разделения трафика в сетях MPLS, в соответствии с которым пропускная способность, требуемая данным потоком трафика от узла к узлу, делится на два непересекающихся пути.
Представлен алгоритмический подход к расчету недоминируемых решений и выбору оптимальных компромиссных решений этой задачи с учетом двух уровней оптимизации. Разрешающий подход начинается с расчета недоминируемых решений относительно целевых функций первого уровня с использованием нового алгоритма [4] и включает определение пороговых значений предпочтений для этих функций с целью установления гибкой системы предпочтений на первом уровне. Затем целевые функции второго уровня просто используются для получения границ для фильтрации
определенного числа наиболее предпочтительных недоминируемых решений первого уровня. Также был проведен ряд вычислительных экспериментов с прикладной моделью, ориентированной на применение маршрутизации видеотрафика, чтобы показать эффективность предложенного алгоритма. Прикладная платформа использовала GT-ITM Georgia Tech Internet-work Topology Models
software1, которая позволила генерировать и анализировать значительное разнообразие случайно генерируемых топологий интернет-сетей, следуя определенным вероятностным законам.
Эта статья организована следующим образом. В разделе 2 подробно описывается предлагаемая многокритериальная модель маршрутизации для двухпутного разделения трафика и соответствующая математическая формулировка. В разделе 3 представлен разработанный подход к разрешению, включающий краткое описание алгоритма, разработанного для нахождения недоминируемых пар разобщенных замкнутых путей, а также модель системы предпочтений. Модель приложения для маршрутизации трафика в случайно генерируемых топологиях интернета и некоторые результаты вычислений приведены в разделе 4. Наконец, в разделе 5 мы приводим некоторые выводы и намечаем дальнейшую работу над этой моделью.
2. Иерархическая многокритериальная модель маршрутизации с разделением трафика
Это область, где существуют потенциальные преимущества во введении подходов маршрутизации с несколькими критериями, принимая во внимание сетевые основные функциональные особенности и природу множественных метрик QoS. Здесь мы начнем с описания природы и цели конкретных целевых функций, участвующих в этой новой иерархической модели многокритериальной маршрутизации для сетей MPLS с двухпутным механизмом разделения трафика.
Первая целевая функция, рассматриваемая на первом уровне оптимизации, – это функция стоимости балансировки нагрузки
, которая представляет собой сумму затрат, связанных с двумя путями, где стоимость балансировки нагрузки дуги является кусочно-линейной функцией пропускной способности, используемой в дуге. Это функция, которая использовалась в предыдущих моделях многокритериальной маршрутизации, а именно в [8] и в модели три критерия для сетей MPLS в [6].
Минимизация этой функции направлена на минимизацию негативного влияния на остальные сетевые потоки в результате использования заданного пути рассматриваемым потоком узел-узел
. Эта функция формализуется следующим образом, для любой пары непересекающихся простых путей, q и q′:
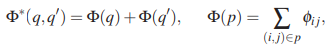
где φij – стоимость балансировки нагрузки, связанная с дугой (i, j), задаваемая
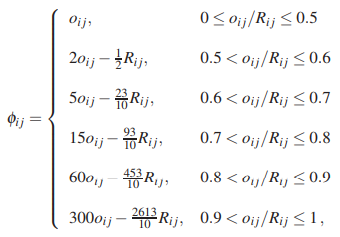
где oij = Rij-bij – полоса пропускания, занимаемая в arc (i,j), а bij – это доступная полоса пропускания в arc (i, j) с емкостью Rij .
Что касается второй целевой функции на первом уровне, то это просто сумма числа дуг в двух путях:
h*(q, q′) = h(q) + h(q′), |
где h(p) обозначает количество дуг пути p. Цель этой функции состоит в том, чтобы искать минимизацию ресурсов, используемых данным потоком трафика, следовательно благоприятствуя пропускной способности сетевого трафика (особенно для высоких нагрузок), а также надежность пути (при отказе ссылок или дуг).
Оптимизация этих двух функций направлена, в приближенном порядке, на минимизацию негативного влияния использования двух путей в остальных потоках трафика в сети. Далее мы рассмотрим две функции для второго уровня приоритета, которые стремятся оптимизировать связанные с передачей параметры QoS для определенного потока от узла к узлу, который маршрутизируется через эти два пути. Первая из этих функций – это минимальная из доступных полос пропускания в соединениях двух путей (узкое место пропускной способности, b), которая должна быть максимизирована:

Эта функция направлена на распределение нагрузки потока через пути с наименее занятыми ссылками.
Вторая функция, рассматриваемая на этом уровне, – это максимальная средняя задержка, наблюдаемая по двум путям, которая должна быть минимизирована:

где dij – средняя задержка пакетов на канале (i, j). Эта функция ищет пары путей с минимальной средней задержкой пакетов.
Что касается ограничений, первый соответствует требованию разделения трафика с использованием двух путей, т. е. сумма полос пропускания узкого места в двух непересекающихся путях не может быть меньше полосы пропускания, требуемой микропотоками (т. е. сквозные соединения с заданными требованиями QoS) рассматриваемого потока от узла к узлу, ∆bandwidth:
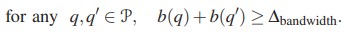
Второе ограничение, которое может быть рассмотрено в модели, является связанным с jitter
ограничением, которое может быть преобразовано для некоторых дисциплин массового обслуживания (а именно для взвешенной дисциплины справедливого массового обслуживания) в ограничение на максимальное число дуг на путь, ∆jitter:
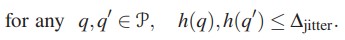
Это ограничение важно для определенных типов потоков трафика QoS (т. е. с гарантированным уровнем качества обслуживания), как в случае видеотрафика, рассматриваемого в модели приложения, и может быть устранено для потоков трафика максимального усилия, для которых нет такой гарантии QoS. Затем может быть сформулирована рассмотренная иерархическая задача маршрутизации с несколькими критериями, обозначающая P множество допустимых путей:
- 1-й уровень
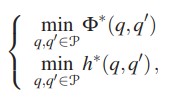
- 2-й уровень
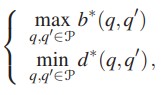
Адресованная иерархическая многокритериальная задача маршрутизации состоит в нахождении удовлетворительных
компромиссных решений (q,q′), q,q′ ∈ P, где q и q′ – непересекающиеся циклические пути с учетом иерархии оптимизации.
3. Подход к решению
В общем случае задача (3) не имеет оптимального решения (пары непересекающихся путей) из-за возможного конфликта между рассматриваемыми функциями первого уровня. Таким образом, необходимо будет рассмотреть множество недоминированных
решений, т. е. решений, таких, что нет другого возможного решения, которое улучшает одну целевую функцию, не ухудшая вторую целевую функцию. Вспоминается определение доминирования в терминах двух функций c и h (которые должны быть минимизированы:
Определение 1: при заданных решениях a и b a доминирует над b (aDb) тогда и только тогда, когда C(a) ≤ c(b), h(a) ≤ h(b) и по крайней мере одно из неравенств строго. Решение b доминирует тогда и только тогда, когда есть другое решение, скажем, такое, что aDb. PN будет обозначать набор недоминируемых решений.
Тогда шаги модификации топологии сети следующие:
- Дублирование узлов: N′ = N∪ {i′:i ∈ N}.
- Дублировать дуги и добавить новую дугу, связывающую t и новую дугу s′: A′ = A∪ {(i′ , j′) : (i, j) ∈ A} ∪ {(t,s′)}.
- Поддержание начального узла: s.
Каждый простой путь p от s до t′ в (N′ ,A′) соответствует паре путей от s до t в (N, A), т. е. существует q ∈ Pst и q′ ∈ P′ s′ t′, такие что
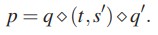
Таким образом, если q∩q′ = /0, то q,q′ соответствуют паре непересекающихся простых путей в (N, A). На рис. 1 в упрощенном виде показано построение модифицированной сети.
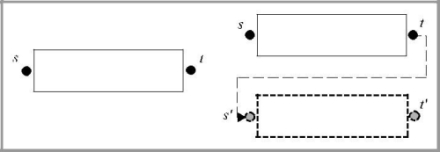
Рис. 1. Оригинальные и соответствующие дополненные сети
Также предполагается, что каждому каналу (i, j) назначается пропускная способность Rij ∈ IR+ (обычно выражаемая в битах/с) и доступная пропускная способность bij.
Первым этапом подхода является решение бикритериальной задачи первого уровня путем вычисления недоминированных решений, заданных адаптацией алгоритма в [3] на основе метода простого ранжирования путей с помощью [9].
Для определения системы предпочтений недоминируемых решений первого уровня следующим этапом алгоритмического подхода является расчет порогов предпочтений, соответствующих требуемым (уровень аспирации) и приемлемым (уровень резервирования) значениям для целевых функций Φ* и h*. Эти пороги используются для определения областей в целевом функциональном пространстве первого уровня с различными требованиями к приоритету , которые позволяют упорядочить кандидатные решения в P′N, наборе недоминируемых путей в (N′, A′). Важно отметить, что рассмотрение этих порогов предпочтения является простым и эффективным способом включения автоматизированного процесса принятия решений, как требуется в этом методе многокритериальной маршрутизации.
Пороговые значения предпочтений можно легко рассчитать в модифицированной сети следующим образом:
- Обязательные (уровень аспирации) и приемлемые (уровень резервирования) значения h, hreq и hacc, соответственно:
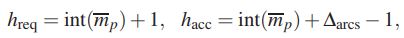
(∆arcs > 2), где int(x) – наименьшее целое число, большее или равное x, а m p-среднее значение допустимых кратчайших длин путей для всех пар узлов в модифицированной сети.
- Необходимые и приемлемые значения Φ, Φreq и Φacc, соответственно:

Поэтому регион с наивысшим приоритетом (регион A, как показано на рис. 2) может определяться точками, для которых удовлетворяются как требуемые значения Φreq, так и hreq. Регионы второго приоритета (B1 и B2 на рис. 2) также могут быть определены точки, для которых удовлетворено только одно из запрошенных значений, при этом не превышен уровень резервирования для другой функции. Также может быть рассчитан регион с третьим приоритетом (C), таким образом, что удовлетворяются только уровни резервирования для обеих функций, в то время как уровни устремления превышаются.
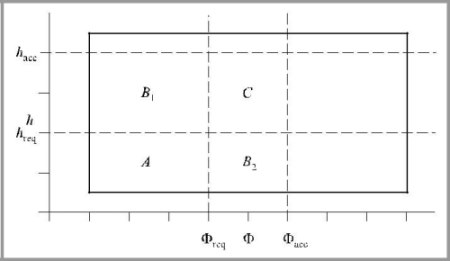
Рис. 2. Приоритетные районы
Наконец, в качестве компромиссного решения проблемы будут выбраны решения первого уровня с более высоким приоритетом, удовлетворяющие этим границам.
Следует отметить, что анализ исключительно недоминируемых решений первого уровня можно считать ограничительным с учетом того, что существует второй уровень оценки критериев. Кроме того, в некоторых случаях может оказаться целесообразным расширить набор возможных компромиссных решений, которые должны быть отфильтрованы на заключительном этапе подхода, основанного на резолюции. Таким образом, аналогично подходу в [2] мы можем рассматривать ε-недоминированные решения на первом уровне, причем значение ε настраивается в соответствии с конкретной средой применения. Кроме того, рассмотрение ε-недоминируемых решений на верхнем уровне оптимизации повышает гибкость модели. Фактически расширение набора анализируемых решений может сопровождаться ужесточением границ, полученных со второго уровня, или наоборот. Таким образом, сочетание вариации ε и границ второго уровня позволяет представить относительную важность обоих уровней на этапе выбора решения. Таким образом, гибкая природа нашей многокритериальной модели может быть усилена.
4. Применение модели и результаты вычислений
Для тестирования иерархической многокритериальной модели маршрутизации и метода разрешения, описанного в предыдущих разделах, была написана программа на языке С, реализующая такой подход, и проведены вычислительные эксперименты для конкретной прикладной задачи.
Представленная модель была применена к проблеме маршрутизации видеотрафика в сети типа MPLS. Топологии сети, используемые для этой цели, где генерируется с помощью программного обеспечения gt-ITM Georgia Tech Internetwork Topology Models
. Это программное обеспечение позволяет вычислять случайно сгенерированные интернет-топологии с различными архитектурами и использовать различные типы законов для определения вероятности появления ребра между любыми двумя заданными узлами, как правило, в виде экспоненциальной функции евклидова расстояния между узлами и некоторыми калибрующими параметрами. Эти модели призваны лучше отражать структуру сетей реального типа интернета. Поскольку мы хотели иметь контроль над средней степенью узла, мы использовали в качестве более адекватного распределения вероятностей ребер модель Доара-Лесли [5]. Это было откалибровано для каждого заданного числа узлов, чтобы получить приблизительно желаемую среднюю степень узла. Рассматриваемой сети 30, 50, 100, 150, 200 узлов, а средняя степень узла 4. Для каждого числа узлов было сгенерировано 10 топологий сети и для каждой сети рассмотрено 20 пар узлов источник-назначение.
В задаче маршрутизации видеотрафика предполагается, что каждый узел моделируется как система очередей с использованием служебной дисциплины взвешенная Справедливая организация очередей (WFQ), что позволяет представить привязку к дрожанию через ограничение на количество дрожаний дуг . Каждую дугу (I, J) был назначен на доступную полосу пропускания bij и средней задержки пакетов dij. Значения bij ∈ {0.52, . . . , 150.52} (в Мбит/с) были случайным по данным эмпирического статистического распределения:

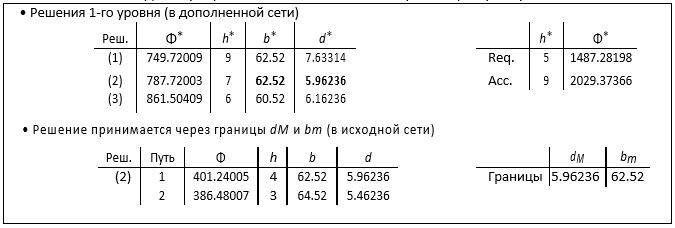
В первом примере сети из 100 узлов (рис. 3a) все решения, найденные на 1-м уровне, (1), (2) и (3), принимаются через границы 2-го уровня. Поэтому выбирается решение (2) в области с более высоким приоритетом.
На примере рис. 3b (в сети с n = 100) было принято только Решение (1), в то время как (2) было отклонено. Обратите внимание, что в этом случае оба решения имеют одинаковое D*, и мы выбрали в качестве связанного bm наиболее требовательное значение b* (62.52). В примере таблицы 3 из 3 решений только решение (2) было принято через границы, полученные на 2-м уровне, так как мы рассмотрели (аналогично предыдущему примеру) наиболее требовательное значение D* как связанное для двух решений (1) и (2) с равным максимальным b*.
Наконец, обратите внимание, что, когда решения с одинаковым значением одной из метрик появляются в списке выбранных путей, при необходимости они могут быть переупорядочены в соответствии с метрикой, которая различает эти решения.

Рис. 3. Решение первого уровня для: (a) первой и (b) второй пары источник-назначение сети из 100 узлов; (c) сети из 200 узлов
Таблица 1 – Решения для первой пары узлов источник-назначение (n = 100), случай рис. 3a
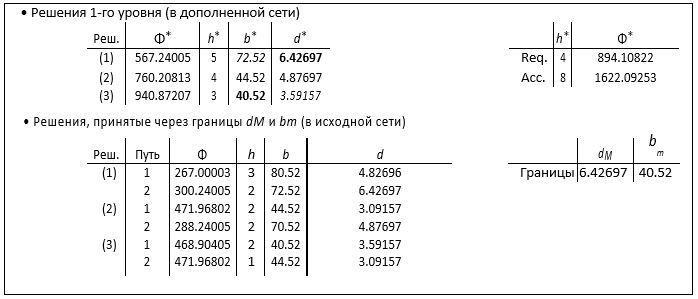
Таблица 2 – Решения для второй пары узлов источник-назначение (n = 100), случай рис. 3b
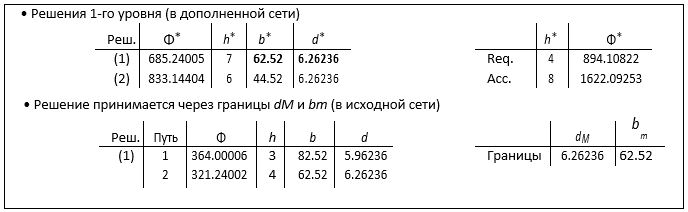
Таблица 3 – Решения для пары узлов источник-назначение (n = 200), случай рис. 3c
5. Заключение
Была представлена новая иерархическая модель многокритериальной маршрутизации, связанная с двухпутным методом разделения трафика в сетях MPLS, в соответствии с которым пропускная способность, требуемая данным потоком трафика от узла к узлу, делится на два непересекающихся пути. Предложен алгоритмический подход к расчету недоминированных решений (или ε недоминированных) на первом уровне и выбору хороших компромиссных решений этой задачи с учетом целевых функций второго уровня. Разрешающий подход начинается с расчета недоминируемых решений по целевым функциям первого уровня с использованием нового алгоритма [4] и включает определение пороговых значений предпочтений для этих функций с целью установления гибкой системы предпочтений на первом уровне. Затем целевые функции второго уровня просто используются для получения границ для фильтрации
определенного числа наиболее предпочтительных недоминируемых решений первого уровня. Этот подход представляется весьма адекватным автоматизированному процессу принятия решений, как того требует система маршрутизации сетей связи, учитывая ее эффективность и гибкость.
Представлены некоторые вычислительные эксперименты с моделью приложения, фокусирующейся на задаче маршрутизации видеотрафика в случайно генерируемых топологиях Интернет-типа, чтобы показать эффективность предлагаемого подхода. Расчет ε недоминируемых решений на первом уровне в сочетании с переменными фильтрующими
границами, определенными на втором уровне, может быть использован в контексте разработанной процедуры с целью повышения гибкости подхода.
1 Доступный в http://www.cc.gatech.edu/...
Ссылки
- J. Climaco and J. Craveirinha,
Multiple criteria decision analy-sis – state of the art surveys
, in International Series in Operations Research and Management Science, J. Figueira, S. Greco, and M. Erghott, Eds. New York: Springer, 2005, pp. 899–951. - J. Climaco, J. Craveirinha, and M. Pascoal, Multicriteria Routing Models in Telecommunication Networks – Overview and a Case Study. Amsterdam: IOS Press, 2007, chapt. 1, pp. 17–46.
- J. Climaco and E. Martins,
A bicriterion shortest path algorithm
, Eur. J. Oper. Res., vol. 11, pp. 399–404, 1982. - J. C. N. Climaco and M. M. B. Pascoal,
Finding non-dominated shortest pairs of disjoint simple paths
, Technical Report, no. 3, INESC-Coimbra, 2007. - M. Doar and I. M. Leslie,
How bad is naive multicast routing?
, in INFOCOM (1), San Francisco, USA, 1993, pp. 82–89. - S. C. Erbas and C. Erbas,
A multiobjective o?-line routing model for MPLS networks
, in Proc. 18th Int. Teletraf. Congr., Berlin, Germany, 2003. - J. Granat and A. P. Wierzbicki,
Multicriteria analysis in telecommu-nications
, in Proc. 37th Ann. Hawaii Int. Conf. Syst. Sci., Hawaii, USA, 2004. - J. Knowles, M. Oates, and D. Corne,
Advanced multi-objecive evolutionary algorithms applied to two problems in telecommuni-cations
, British Telecom Technol. J., vol. 18, no. 4, pp. 51–65, 2000. - E. Martins, M. Pascoal, and J. Santos, Deviation algorithms for ranking shortest paths, Int. J. Foundat. Comput. Sci., vol. 10, no. 3, pp. 247–263, 1999.
- C. Pornavalai, G. Chakraborty, and N. Shiratori,
Routing with multiple QoS requirements for supporting multimedia applications
, Telecommun. Syst., vol. 9, pp. 357–373, 1998.