В настоящее время на рынке транспортных услуг конкуренция приобретает качественно новые черты: на фоне повышения затрат на перевозку, ужесточения требований к автотранспортным средствам повысились требования к качеству перевозочного процесса. В таких условиях функционирование предприятия невозможно без наличия эффективной системы управления.

Создание маршрутов позволяет точно определить объем перевозок грузов, количество автомобилей, осуществляющих эти перевозки, способствует сокращению простоя автомобилей под загрузкой и разгрузкой, эффективному использованию подвижного состава и высвобождению из сфер обращения значительных материальных ресурсов потребителей. Если созданы оптимальные маршруты и соблюдаются сроки поставки, то производственные запасы потребителей могут сокращаться в 1.5-2 раза, снижая тем самым затраты на складирование. Необходимость маршрутизации перевозок грузов обосновывается еще и тем, что маршруты дают возможность составления проектов текущих планов и оперативных заявок на транспорт, исходящих из действительных объемов перевозок. Таким образом, разработка обоснованных маршрутов и проектов планов перевозок способствует своевременному и бесперебойному выполнению поставок продукции и эффективному взаимодействию организаций-поставщиков, организацийполучателей и автотранспортных организаций.

Подводя итог вышесказанному можно с уверенностью сказать, что задача оптимизации маршрутизации транспортных средств становится особо актуальной в условиях данной экономической ситуации.

В данный момент многие ведущие фирмы, организации работают в области транспортной логистики, пытаясь усовершенствовать существующие системы, что позволит получить еще большую производительность алгоритмов. Для решения данной задачи был разработан ряд методов, алгоритмов и подходов. Среди них можно выделить метод Кларка-Райта [1], эвристические методы вставок, табу-поиск [1], метод ветвей и границ, метод ветвей с отсечениями, муравьиные [2] и генетические алгоритмы. Однако они обладают некоторыми недостатками. Учитывая жадный характер алгоритма Кларка-Райта, полученные решения имеют часто недостаточное качество относительно более сложных подходов. Не следует также ожидать, что эвристические алгоритмы вставки для любых исходных данных найдут решения в равной степени близкие к оптимальному. Механизм табу-поиска, заключающийся во введении штрафов за нарушение всех видов ограничений в целевую функцию, не дает гарантий нахождения допустимых решений. Метод ветвей и границ и метод с отсечениями не эффективны по времени выполнения и во многом зависят от начальных установок, а также не применимы к задачам большой размерности.

Задача маршрутизации транспортных средств (ЗМТ) является сложной комбинаторной задачей оптимизации. Данную задачу с ограничением по времени и грузоподъемности можно описать следующим образом [3].

Имеется один центральный склад , который использует некоторое количество независимых транспортных средств поставки с идентичной грузоподъемностью для обслуживания спросов от клиентов, . Для каждого транспортного средства требуется составить маршрут, по которому оно может обслуживать ряд клиентов, при чем каждый клиент должен быть обязательно обслужен только одной машиной. Имеется матрица расстояний между клиентами и складом и рассчитанная себестоимость одного километра пути с учетом расходов на топливо, техническое

обслуживание машин, зарплаты водителям и др. На основании этих данных рассчитывается матрица стоимости расстояний между клиентами и складом. Транспортные средства должны выполнить поставки с минимальной полной стоимостью длины всех маршрутов S, Стоимость расстояний между клиентами симметрична, то есть, cij-cji (cii = 0), где cij является стоимостью расстояния от клиента i до клиента j, где i,j ? [0..N]. Решение для ЗМТ может быть представлено в виде разделения N спросов в K маршрутах {R1,...,Rk}, K?min, причем каждый маршрут начинается и заканчивается на складе. Тогда задача оптимизации грузовых перевозок может быть сформулирована как минимизация общей стоимости всех маршрутов с учетом выполнения ограничений:

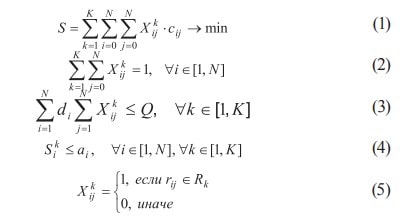
где rij – подмаршрут от клиента i к клиенту j, верхним индексом k обозначаться соответствующий маршрут, где k ? [1..K], K – количество маршрутов.

Ограничение (2) полагает, что каждый клиент обслуживается только одним транспортным средством и только один раз. Ограничение (3) определяет, что транспортное средство не может обслужить больше клиентов, чем позволяет его грузоподъемность. di – спрос соответствующего клиента, N – количество клиентов. Ограничение (4) – это ограничение по времени; прибытие машины к клиенту не должно быть позднее установленного срока.Sik – это время прибытия соответствующей машины k к клиенту i, ai – крайний срок времени обслуживания клиента i.

В качестве алгоритма решения задачи оптимизации грузовых перевозок было предложено использовать новый усовершенствованный эвристическими методами генетический алгоритм с модифицированными проблемно-ориентированными операторами. Учитывая характер задачи генетический материал особи должен содержать несколько маршрутов, каждый из которых составлен из упорядоченного подмножества клиентов. Как пример, хромосома на рис. 1 кодирует решение, представленное на рис. 2.

Начальная популяция формируется эвристическим методом Кларка-Райта и ?-перестановками, позволяющими получить окрестность решения. Для оценки качества полученных решений (хромосом) будем использовать следующую фитнес-функцию:

где ?i – штраф, связанный с нарушением временных ограничений для клиента i. Если поставка запланирована в срок, то штраф равен нулю, иначе он растет с увеличением задержки времени обслуживания.

Оператор селекции основывается на методе ранжирования, в котором вероятность отбора для каждой особи зависит только от её позиции (номера) в упорядоченном по значению целевой функции множестве особей, а не от самого значения фитнес-функции.

Рисунок 1 - Пример кодирования решения в хромосоме

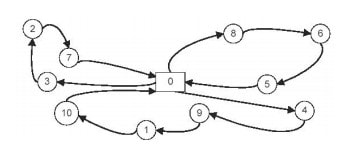
Рисунок 2 - Пример решения ЗМТ

Для создания потомков бы разработан модифицированный оператор кроссинговера, учитывающий специфику исследуемой задачи. Количество родителей, участвующих в скрещивании обозначается параметром M. увеличение данного параметра позволяет более эффективно передавать свойства (маршруты) родителей потомкам, сходимость алгоритма увеличивается, но это грозит опасностью попадания в локальный минимум. При уменьшении M растет разнообразие в популяции. Оптимальное значение параметра варьируется в пределах от 2 до 4. Оператор кроссинговера заключается в следующем:

1. Маршруты из выбранных особей объединяем в одно решение. Данное решение назовем объединенным.
2. Пока в объединенном решении есть маршруты, делаем следующее: выбираем маршрут и вставляем его в новое решение, для этого берем случайное число в пределах от 0 до количества маршрутов в объединенном решении, данное число и будет указывать номер маршрута в объединенном решении; удаляем выбранный маршрут в объединенном решении; удаляем в объединенном решении все маршруты, в которых есть клиенты из выбранного решения.
3. Вставляем не обслуженных клиентов в новое решение с использованием метода самого дешевого включения с учетом грузоподъемности. Если вставка не возможна – создается новый маршрут.

На основании анализа современных исследований ведущих ученых в области вопроса об оптимальной маршрутизации транспортных средств и особенностей данной задачи был предложен ряд операторов мутации, которые применяются с соответствующими вероятностями.

1. обмена: в хромосоме выбирают двух клиентов и меняют их. Выбранные узлы могут принадлежать одному и тому же или различным маршрутам. Вероятность данного оператора – 2%;
2. инверсии: выбирают подмаршрут и реверсируют порядок принадлежащих ему клиентов. Вероятность данного оператора – 2%;
3. перемещения: выбирают подмаршрут и вставляют его в другое место. Этот оператор может выполнить внутреннее или внешнее перемещение. Вероятность данного оператора – 2%;
4. вторичной вставки клиентов: из решения удаляются отдельные клиенты, и затем заново вставляются в маршрут. Вероятность данного оператора – 15%;
5. вторичная вставка маршрутов: из решения удаляются маршруты целиком, затем клиенты с удаленных маршрутов заново вставляются в решение. Вероятность данного оператора – 15%;
6. переупорядочивание клиентов: - процедура интенсификации, которая пытается уменьшить полное расстояние допустимых решений, переупорядочивая клиентов в пределах маршрута с помощью усовершенствованного эвристического метода Вероятность данного оператора – 15%.

Оператор корректировки направлен на исправление нарушений ограничений для недопустимых решений. Он удаляет из маршрутов клиентов, которые нарушают ограничения, и пытается повторно вставить их в другой маршрут так, чтобы сформировать допустимое решение. В случае, если это невозможно – создается новый маршрут.

Оператор редукции отбирает в новую популяцию 15% элитных хромосом, затем методом рулетки формируем недостающее количество особей.

В качестве критерия останова используется отсутствие улучшения значения фитнес-функции на протяжении пяти итераций.

Программная реализация усовершенствованного генетического алгоритма для оптимизации грузовых перевозок была выполнена на языке высокого уровня в среде С++ Builder 6.0 [5]. В результате проведенных экспериментальных исследований с использованием реальных данных с помощью предложенного подхода получен набор оптимальных маршрутов, которые представляются в виде маршрутных листов с указанием необходимых данных о заказах и клиентах.

Для оптимизации значений параметров предложенного алгоритма было проведено экспериментальное тестирование программы на наборе реальных данных, который включает 100 клиентов, расположенных на территории Украины. По результатам исследований были составлены графики (рис. 3 и 4).

Графики свидетельствуют о том, что рациональная мощность популяции находится в интервале от 60 до 80, а вероятность кроссинговера – в интервале от 0.6 до 0.8.

Была выполнена программная реализация предложенного алгоритма и проверена адекватность эволюционной модели. Завершающим этапом стало проведение экспериментальных исследований с целью выявления рациональных значений параметров генетического алгоритма и оценки эффективности оптимизации грузовых перевозок. Проведенные исследования показали целесообразность и эффективность применения данного подхода в оптимизации грузовых перевозок. Были предоставлены практические рекомендации по формированию маршрутов для работы транспортного предприятия.

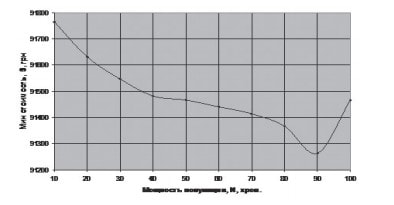
Рисунок 3 – График зависимости минимальной стоимости маршрутов от мощности популяции

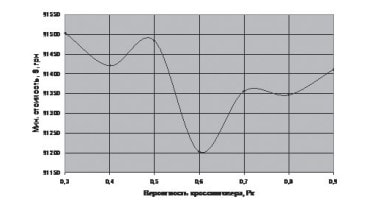
Рисунок 4 – График зависимости минимальной стоимости маршрутов от вероятности кроссинговера

Литература

1. Clarke G. Scheduling of vehicles from a central depot to a number of delivery points / G. Clarke, J.W. Wright // Journal of Operations Research Society. - 1964. – Vol.12, № 4. – pp. 568–581.
2. Макконелл Дж. Основы современных алгоритмов: учебное пособие / Дж. Макконелл; пер. с англ. С.К. Ландо. – [3-е изд.]. - М.: Техносфера, 2004. — 368 c.
3. Смехов А.А. Основы транспортной логистики. / А.А. Смехов. - М.: Транспорт, 1995. - 197 с.
4. Рутковская Д. Нейронные сети, генетические алгоритмы и нечеткие системы / Д. Рутковская, М. Пилиньский, Л. Рутковский; пер. с польск. И.Д. Рудинский – М.: Горячая линия-Телеком, 2006. – 452 с.
5. Архангельский А.Я. Программирование в C++Builder 6 / А.Я. Архангельский. – М.: БИНОМ, 2003. – 1152 с.