Аннотация

Эта работа представляет собой вклад в сравнение двух метаэвристических алгоиртмов, основанных на природных принципах для решения задачи коммивояжера. Мы запускаем муравьиный алгоритм (МА) и генетический алгоритм (ГА) на трех контрольных экземплярах с различным размером и сложностью, в дополнение к одному реальному приложению в сфере городского транспорта и логистики. В первой главе представлены алгоритмические подходы. Глава результатов и обсуждения описывает вычислительное поведение алгоритмов на протяжении всего решения задачи. Заключение закрывает обсуждение с рекомендациями и будущими областями применения.

Ключевые слова

Задача коммивояжера, Генетические алгоритмы, Муравьиные алгоритмы

1. Введение

Подавляющее большинство инженерных проблем может быть выражено в общей форме задачи оптимизации, в которой целевая функция или функция стоимости определены, то есть минимизированы по отношению ко всем вовлеченным ограничениям. Например, широко изученная задача коммивояжера, где целью является минимизация общего расстояния в одном замкнутом туре, посещая каждый город один раз. K. Менгер [1] был одним из первых исследователей, которые обратились к задаче коммивояжера и изучитли ее подробно. Евклидова задача коммивояжера является частным случаем задачи, в которой города имеют координаты в евклидовом плане [2].

Было доказано, что эта задача является NP-трудной [3], решение ее потребует использования очень эффективных алгоритмов, поэтому мы выбираем использование двух известных алгоритмических подходов: муравьиные и генетические алгоритмы. Задача коммивояжера в реальном мире – более общий случай, когда города представлены в системе географических координат.

Эти два подхода называются метаэвристикой. В общем-то, метаэвристика широко применяется ко всем аспектам комбинаторной оптимизации. В этом подвиде алгоритмов также есть такие подходы, как Табу-поиск, метод моделирования отжига [4], алгоритм роевой оптимизации и эволюционное программирование. Все они стремятся обеспечить достаточно хорошие решения сложных задач проблемы [5] [6].

Эта работа направлена на сравнение МА и ГА при решении различных экземпляров знаменитой задачи коммивояжера (ЗК) [7] [8], для этого мы используем один асимметричную задачу коммивояжера для реального мира из комплекса городских среда города Касабланка и три тестера производительности Евклидовой симметричной ЗК с возрастающей сложностью. Эта работа структурирована следующим образом: вторая глава описывает современное состояние реализованных методов, третья глава представляет результаты различных симуляций и последняя глава содержит выводы по этой работе.

2. Современное состояние проблемы

2.1 Генетический алгоритм

Концепция ГА была впервые представлена Холлендом и его коллегами в конце 1960-х годов [8]. ГА вдохновлены эволюционной теорией.

В природе непригодные и слабые виды в окружающей среде сталкивается с исчезновением посредством естественного отбора. Самые сильные виды имеют больше возможностей для передачи их генов для будущих поколений путем воспроизводства; Этот процесс занимает много времени. В долгосрочной перспективе виды, несущие правильную комбинацию генов, становятся все более доминирующими [9].

Иногда, во время этого медленного процесса эволюции, случайные изменения могут происходить с генами. Эти непреднамеренные изменения могут предложить дополнительные преимущества для процесса естественного отбора через диверсификацию. В этом бесконечном испытании выживания, новые виды развиваются из старых, неудачные изменения и комбинации автоматически исключаются естественным отбором [10] [11].

В терминологии ГА вектор решения называется особь или хромосома. Эти хромосомы сделаны из дискретных единиц, называемых генами. Каждый ген контролирует один или несколько элементов хромосомы. Оригинальная реализация ГА от Holland имела двоичные цифры в качестве ген [8]. Самая последняя реализация принесла большее разнообразие представления и кодировки генов.Обычно хромосома является уникальным решением в пространстве решений. ГА работает с набором хромосом, называемых популяцией. Популяция обычно инициализируется случайным образом.Поскольку алгоритм работает, он постепенно находит особей с более высокой приспособленностью; у каждого кандидата есть набор свойств(генотип), который может быть видоизменен, что повышает вероятность поиска лучших решений [12]. Алгоритм завершается, когда критерий был выполнен (максимальное количество итераций или достигнут удовлетворительный уровень фитнесс-функции). На рисунке приведен псевдокод ГА:

2.2 Муравьиный алгоритм

Алгоритм оптимизации колонии муравьев основан на метаэвристических агентах, которые используются для поиска решений различных проблем оптимизации. Агенты называются искусственными муравьями. Эти алгоритмы были вдохновлены поведением муравьев и составляют с другими вдохновленными роем алгоритмами большое семейство оптимизационной метаэвристики [13].

Алгоритм является результатом тщательного наблюдения за поведение социальных насекомых вообще и муравьев в частности. Муравьи являются социальными насекомыми, и они ведут себя коллективно направлены на благо колонии. Каждый муравей независимый и общается с другими муравьями через летучие химические вещества под названием феромон [14].

Муравьи очень чувствительны к этим веществам и используют их чтобы обозначить их путь, чтобы быть обнаруженным их товарищами по гнезду. Наиболее распространенным примером является путешествие от гнезда до еды источники, при обнаружении источника; это откладывает феромоны на земле через его брюшные железы. Каждый новый муравей может легко следовать по этому пахучему следу, который приведет его к источнику еды, а затем в гнездо. Таким образом, каждый муравей косвенно и коллективно помогает сообществу [15].

Доступно несколько вариантов МА. Первый МА назывался муравьиной системой (МС) от Dorigo et al. [16]. Формально, муравей к расположенный в городе я в момент времени t выберет следующий город j в зависимости от видимости ? этого города и количества нанесенный феромон ? на дугу, соединяющую эти два города, другие алгоритмические варианты используют другие практики распределения феромона [7] [15]. Выбор следующего города сделан стохастически, с вероятностью выбора города j в качестве следующего :

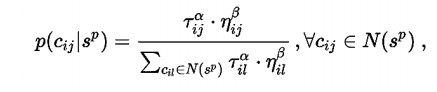
На рисунке приведен псевдокод МА:

2.3 Задача коммивояжера

Задача коммивояжера является одной из наиболее изученных задач вычислительной математики. Это NP-сложная задача и из-за ее простой формализации, она часто используется в качестве эталонного теста для многих методов оптимизации [17].Задача заключается в следующем: учитывая набор городов и расстояния между ними, найти кратчайший путь, который проходит через каждый город ровно один раз и возвращается в исходный город (привести суммарное расстояние).

Задача может быть представлена в виде взвешенного графа, где ребра - города, а дуги - расстояния между ними. Задача может быть симметричной, это общий вид этой задачи, где расстояние от города i до города j такое же, как и от j к i. В этом случае взвешенный граф называется ненаправленным. Другой формой задачи коммивояжера является асимметричная или направленный взвешенный граф, где дуги могут не существовать или иметь разные весы в противоположных направлениях. Асимметричную ЗК можно найти в нескольких реальных приложениях в основном в области логистики, планирования и секвентирования ДНК [2] [17] [18].

Чтобы проверить алгоритмические подходы, мы решили запустить несколько экспериментов, варьирующих сложность и тип ЗК. Два алгоритма проверены на трех тестовых экземплярах и одной реальное мировой асимметричной задаче. Большинство из задач для тестов можно найти в TSPLIB:http://www.iwr.uni-heidelberg.de/iwr/comopt/soft/TSPLIB95 / TSPLIB.html. Проверочными для ЗК являются Berlin52, Eil76 и A280. Приложение реального мира - Casablanca40[19] [20].

TSPLIB предлагает координаты для задачи, лучший тур и оптимальные решения для трех тестовых задач [19].Casablanca40 отличается; проблема асимметрична и учитывает географическую конфигурацию и архитектуру города [20].Город является экономически и демографически самым крупным в Марокко и характеризуется большими транспортными потоками и очевидными проблемами с маршрутизацией транспортных средств.

3.Эксперимент и анализ результатов

Все моделирования были выполнены на персональном компьютере с 64 разрядной ОС Windows с процессором i5-3470 с тактовой частотой 3,20 ГГц и 4 ГБ оперативной памяти. Генетический алгоритм был разработан на C++ с использованием GAlib [21]. Муравьиный алгоритм оптимизации был написан на C#.

3.1 Генетический алгоритм

3.1.1 Berlin52

Первый экземпляр для тестирования ГА - Berlin52 с 52 локациямив Берлине (Groetschel) [19]. Генетический алгоритм находит оптимальный тур за 3,485 секунды. На рис. 1 представлена эволюция целевой функции (здесь расстояние) с течением времени. Рис 8 (а)показывает найденный тур, совпадающий с оптимальным туром экземпляра, оба тура 7542.

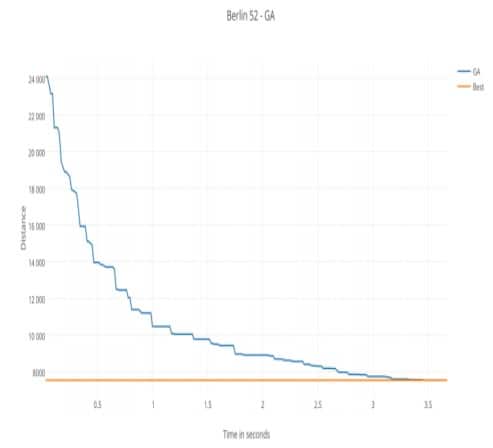
Рис.1 - Эволюция результатов ГА с течением времени на данных Berlin52

3.1.2 Eil76

Второй экземпляр - Eil76 с 76 городами. это считается ЗК большой размерности[19]. ГА дает удовлетворительные результаты, но не находит оптимального решения. Рис 8 (б) иллюстрирует различия между оптимальным туром 538 и туром ГА.Время сходимости значительно меньше. ГА возвращает лучший тур из 570 за 13,441 секунды. С приблизительной ошибкой 5,9479%.

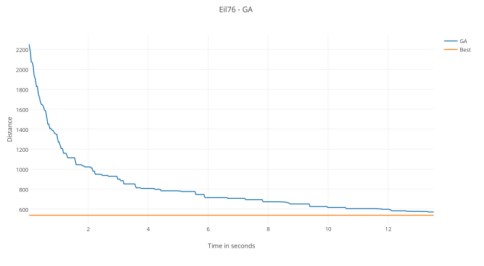
Рис. 2. Эволюция результатов ГА с течением времени в Eil76.

3.1.3 A280

Самый большой пример в этой статье имеет 280 городов, его оптимальный тур 2579 [19]. Из-за своей сложности этот экземпляр требует больше вычислительного времени и точной настройки. ГА обрабатывает этот случай с постоянным фактором улучшения как видно на рис 3 и возвращает лучший тур 3218 в 517,965 секунд. С ошибкой 24,777%.

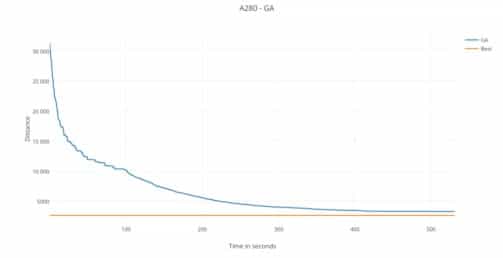
Рис. 3. Эволюция результатов ГА с течением времени в A280.

3.1.4 Casablanca40

Этот случай является частным случаем ЗК применительно к логистике, более конкретно к городской транспортировке [20]. Маршруты представлены в виде ориентированного взвешенного дизъюнктивного графа; результатом будет один тур, который пройдет по всем 40 пунктам задачи. У дизъюнктивного графа 1560 дуг, соединяющих 40 вершин. Общее накопленное расстояние дуг составляет 16273,18 километров. Пространство решений содержит теоретически 2.04E + 46 возможных решений. GA возвращает лучший тур 125,974 километров менее чем за 24,759 секунд. Возвращенный Тур иллюстрируется на рис. 5.

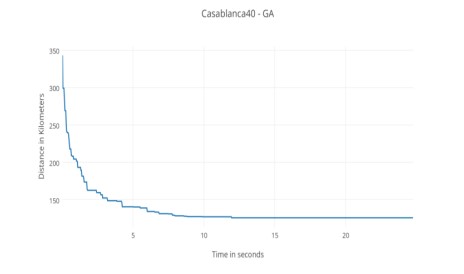
Рис. 4. Эволюция результатов ГА с течением времени в Casablanca40.

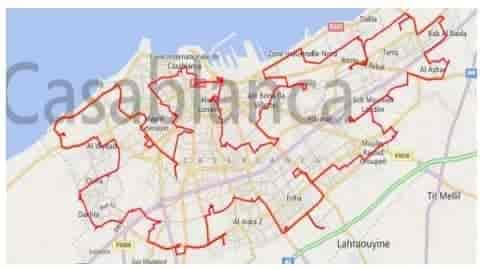
Рис5 - Карта визуализации тура, возвращенного ГА

3.2 The Ant Colony Optimization

3.2.1 Berlin52

Муравьиный алгоритм сходится быстро, но не находит оптимальный тур.Он находит тур длиной 7575 в 17.727 с погрешностью 0,4375% от оптимального тура. Рис 6 показывает эволюцию целевой функции с течением времени. Эволюция может быть разделена на две основные фазы: первая фаза, где алгоритм быстро сходится и находит решение расстояния 7680 менее чем за 3,568 секунды, это поведение близко к таковому в ГА. Второй этап, где нет улучшения до секунд 16,619 и 17,727 с соответственно минорными улучшения на 0,2218% и 1,1617%.

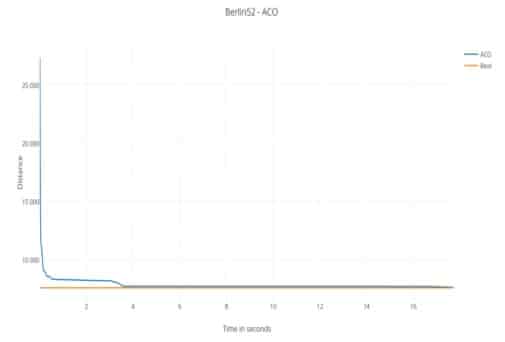
Рис.6 - Эволюция результатов МА с течением времени на данных Berlin52

Этот второй этап обусловлен высоким содержанием феромонов на маршрутах, которые приводят к ранней сходимости, сопровождаемой фазой застоя. Поздние незначительные улучшения могут быть объяснены испарением феромона, которое привело к позднему расхождению обнаруженных путей.

3.2.2 Eil76

Для Eil76 оптимальный тур 538. МА поддерживает те же две фазы поведения; он быстро сходится к туру 588 в 4.886 секунд. С ошибкой 9,2936%. Затем возвращает общий лучший тур 551 после 73,906 секунд с погрешностью 2,4163%. Рис 8 (б) иллюстрирует производительность МА в предоставлении почти оптимального тура.

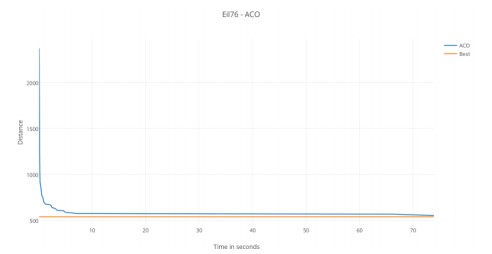
Рис. 7. Эволюция результатов МА с течением времени в Eil76.

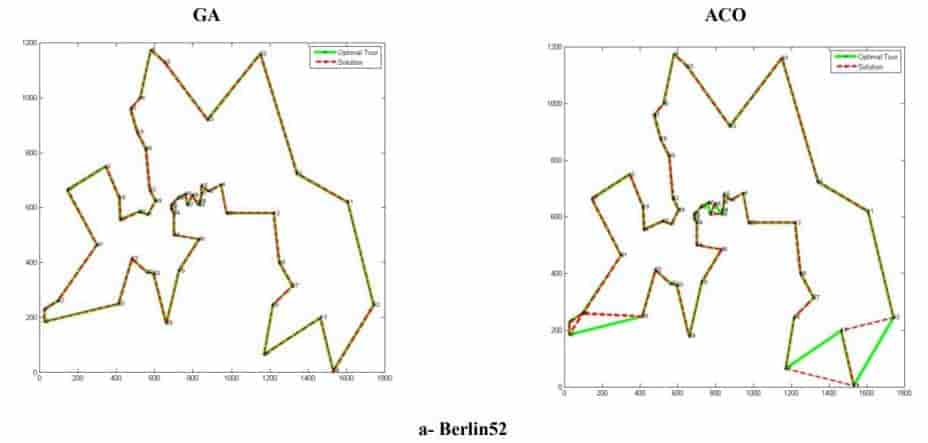
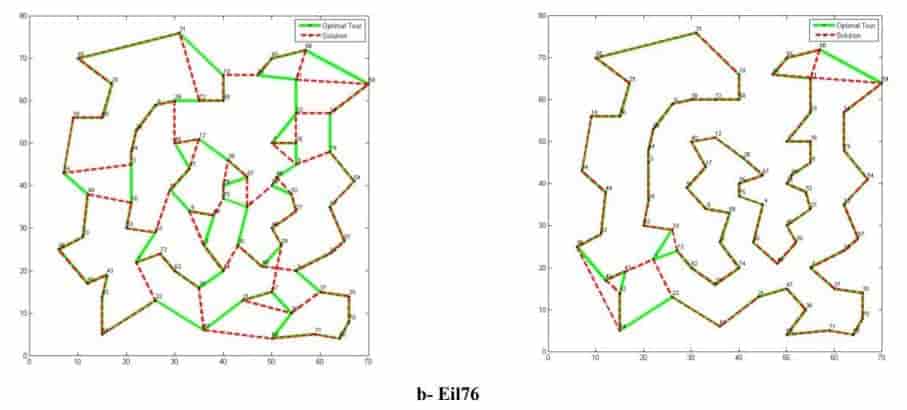
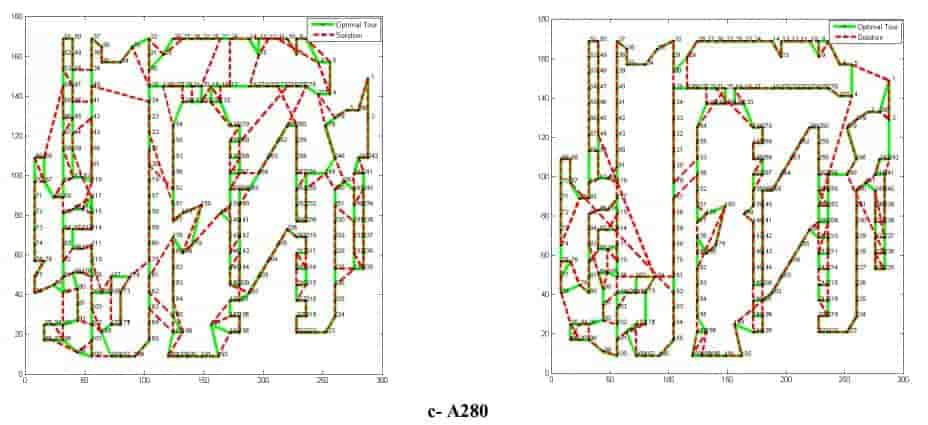
Рис. 8. Результаты ГА и МА по сравнению с оптимальными турами

3.2.3 A280

Этот экземпляр большой и поведение МА немного изменилось. Средняя фаза может наблюдаться между секундами 45,717 и 323,242. Эта фаза характеризуется медленным, но устойчивым коэффициентом улучшения и отсутствием какого-либо застойного поведения. В конце выполнения возвращено лучшее значение тура 3092 за 767,711 секунд с частотой ошибок 19,8914%.

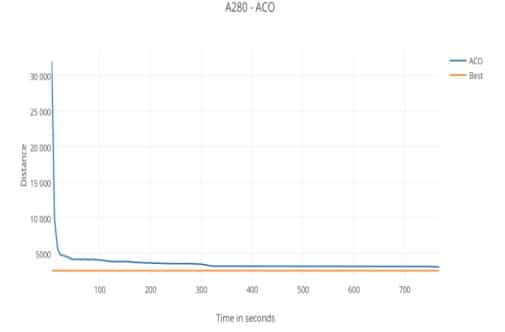
Рис. 9. Эволюция результатов МА с течением времени в A280.

3.2.4 Casablanca40

Последний пример тестирования МА - это Casablanca40 [20].Там нет математически доказанного оптимального тура этой задачи реального мира, лучший тур у нас является результитом, найденным ГА ранее. МА заканчивается очень быстро и достигает лучшего решения расстояния 125,216 за 20,618 секунд. МА качественно лучше на 0,6053%, и вычисляет на 20,0843% быстрее. Актуальный лучший тур по Casablanca40 показан на рис.11.

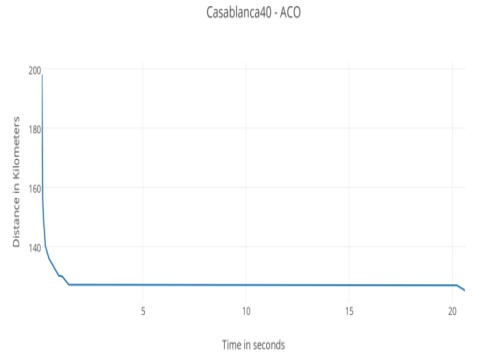
Рис. 4. Эволюция результатов МА с течением времени в Casablanca40.

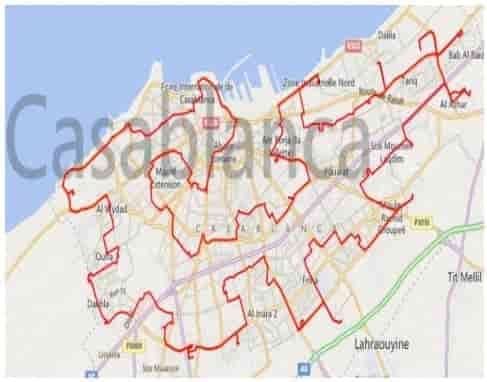
Рис5 - Карта визуализации тура, возвращенного ГА

Таблица 1. Результаты моделирования

Пример		ГА			МА
Название	Лучше решение	Тур	Погрешность, %	Время, с	Тур	Погрешность, %	Время, с
Berlin52	7542	7542	0.0	3.673	7575	0.4375	17.727
Eil76	538	570	5.9479	13.519	551	2.4163	73.906
A280	2579	3218	24.7770	531.087	3092	19.8914	767.711
Название		Тур		Время, с	Тур		Время, с
Casablanca40		125.974		24.759	125.216		20.618

3.3 Сравнение результатов

Качественные и количественные сравнения были сделан, чтобы сравнить эти два алгоритмических подхода. Оба алгоритма дают хорошие результаты в обработке этой NP-сложной задачи оптимизации. Они оба эффективны в решении всех случаев ЗК. Где пространство поиска большое, сложное, плохо изученное и не было проведено никакого предварительного математического анализа. Таблица 1 показывает результаты расчетов.

Оба алгоритма обеспечивают удовлетворительные результаты на четырех тестах; они показывают адекватную производительность на небольших тестах и устойчивость на средних и больших.

GA отлично подходит для малых и средних экземпляров;без каких-либо предварительных знаний о пространстве решения или помощи любой локальной процедуры поиска, она обеспечивает быструю сходимость и поиск оптимальных решений. Во всех случаях алгоритм является надежным и поддерживает постоянное улучшение поведение, он всегда дает решения и решения становятся лучше с течением времени.

МА дает лучшие результаты в больших случаях. Даже со своим значительная производительность по сравнению с GA. Склонен к схождению в локальном оптимуме, потому что он обновляет феромон в соответствии с текущим лучшим путем [13]. Но, учитывая достаточно времени для испарения феромонов, как видно на рис. 13, МА обеспечивает поиск лучших результатов, чем ГА. И скорость сходимости выше на ранних итерациях.

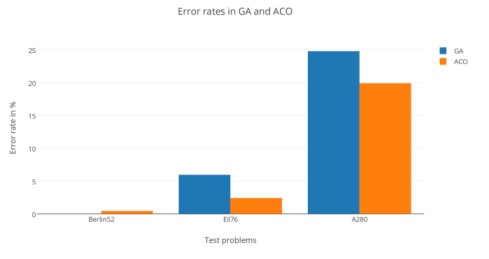
Рис12 - Погрешности в ГА и МА

Когда дело доходит до вычислительных затрат, тщательное сравнение показывает, что МА сходится раньше и поддерживает исследовательское поведение в течение всего доступного времени выполнения. ГА гарантирует устойчивое улучшение поведения и как только он застаивается, он перестает загружать процессор. Во время выполнения, МА более жадный из-за его приспособленности для распределенной обработки [16].

На рис.13 показана погрешность алгоритмов, результаты теста Casablanca40 были опущены, потому что логистическая задача в реальном мире не имеет математически проверенного оптимального тура, и два подхода вернули почти одинаковые туры.

Понятно, что частота ошибок увеличивается со сложностью задачи.Когда количество городов меньше, ГА дает лучшие результаты,когда число городов и пространство решения больше МА превосходит ГА по качеству результатов. Разница в частотах ошибок между двумя алгоритмами выше с увеличением размерности задачи, таким образом, преимущество у МА.

4. Заключение и планы на будущее

В этом документе представлено сравнение качественных и временных характеристик двух известных метаэвристик: ГА и МА. Хотя оба алгоритма обеспечили удовлетворительные результаты по всем тестовым задачам, несколько замечаний приведены ниже.

ГА является быстрым, простым в реализации и экономически эффективным с точки зрения вычислительных ресурсов. МА жаднее, но обеспечивает лучшие результаты, особенно на задачах большой размерности.

На основании результатов нашего моделирования мы рекомендуем:

• ГА для малых вычислительных ресурсов и / или задач малого и среднего размера. Подходит для быстрого нахождения оптимальных решений. Его легко разрабатывать и реализовывать.
• МА для больших вычислительных ресурсов и / или задач большой размерности. Подходит для поиска качественных решений в заметном времени выполнения. Является распределенным, легко приспосабливается к другим алгоритмам.

Два алгоритмических подхода имеют большой потенциал врешение многих реальных приложений на основе ЗК, начиная от логистика для производства и заканчивая робототехникой. Будущие исследования будут сосредоточены на поиске более эффективных производных и комбинации этих алгоритмов.

Алгоритмы очень чувствительны к изменению параметров. В данной работе, мы основывались на опыте авторов в настройке алгоритмов чтобы обеспечить наилучшие результаты. Будущая работа может быть ориентирована на автоматическую адаптацию параметров подпрограммы, основанных на типе задачи и других доступных данных.

5. Список использованных источников

1. K. Menger, Ergebnisse eines mathematischen Kolloquiums: Deuticke, 1932.
2. A. Punnen, "The Traveling Salesman Problem: Applications, Formulations and Variations," in The Traveling Salesman Problem and Its Variations. vol. 12, G. Gutin and A. Punnen, Eds., ed: Springer US, 2007, pp. 1-28.
3. C. H. Papadimitriou, "The Euclidean travelling salesman problem is NP-complete," Theoretical Computer Science, vol. 4, pp. 237-244, 1977.
4. P. Siarry, "La m?thode du recuit simul?: th?orie et applications," Automatique-productique informatique industrielle, vol. 29, pp. 535-561, 1995.
5. H. El Hassani, J. Benhra, and S. Benkachcha, "Utilisation des algorithmes g?n?tiques (AG) dans l’Optimisation multi-objectif en logistique avec prise en compte de l’aspect environnemental (?missions du CO2)," in Colloque international LOGISTIQUA, RABAT, 2012.
6. TALBI, El-Ghazali. Metaheuristics: from design to implementation. John Wiley & Sons, 2009.
7. M. Dorigo and L. M. Gambardella, "Ant colony system: a cooperative learning approach to the traveling salesman problem," IEEE Transactions on Evolutionary Computation, vol. 1, pp. 53-66, 1997.
8. J. H. Holland, "Adaption in Natural and Artificial Systems," The University of Michigan Press, 1975.
9. L. J. Fogel, A. J. Owens, and M. J. Walsh, Artificial Intelligence Through Simulated Evolution: John Wiley & Sons, 1966
10. D. B. Fogel, "The evolution of intelligent decision making in gaming," Cybernetics and Systems, vol. 22, pp. 223-236, 1991.
11. L. D. Davis, Handbook Of Genetic Algorithms, 1 ed.: Van Nostrand Reinhold;, 1991.
12. M. Vazquez and L. D. Whitley, "A Hybrid Genetic Algorithm for the Quadratic Assignment Problem," in GECCO, 2000, pp. 135-142.
13. M. Dorigo, V. Maniezzo, and A. Colorni, "Ant system: optimization by a colony of cooperating agents," Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, vol. 26, pp. 29-41, 1996.
14. T. St?tzle and H. H. Hoos, "MAX–MIN ant system," Future generation computer systems, vol. 16, pp. 889- 914, 2000.
15. A. Colorni, M. Dorigo, and V. Maniezzo, "Distributed optimization by ant colonies," in Proceedings of the first European conference on artificial life, 1991, pp. 134-142.
16. G. Gutin and A. P. Punnen, The traveling salesman problem and its variations vol. 12: Springer Science & Business Media, 2002.
17. ] SHIN, Soo-Yong, LEE, In-Hee, KIM, Dongmin, et al. Multiobjective evolutionary optimization of DNA sequences for reliable DNA computing. Evolutionary Computation, IEEE Transactions on, 2005, vol. 9, no 2, p. 143-158.
18. G. Reinelt, "TSPLIB—A Traveling Salesman Problem Library," ORSA Journal of Computing, vol. 3, pp. 376- 384, 1991.
19. A. H. Sabry, A. Bacha, and J. Benhra, "A contribution to solving the traveling salesman problem using ant colony optimization and web mapping platforms Application to logistics in a urban context," in Codit'14, Metz, France, 2014.
20. WALL, Matthew. GAlib: A C++ library of genetic algorithm components. Mechanical Engineering Department, Massachusetts Institute of Technology, 1996, vol. 87, p. 54.