Аннотация
Довидович В.С. В.В., Мартыненко Т.В. Анализ методов моделирования автомобильного трафика. В статье рассмотрена проблема загруженности автомобильных дорог. Проведена классификация и анализ существующих методов моделирования транспортного потока. Определен подходящий метод моделирования транспортного потока на перекрестке для дальнейшей его оптимизации.
Ключевые слова:
транспортный поток, светофор, моделирование, автомобильный трафик.
Введение
В современном обществе многим людям невозможно представить жизнь без дорожного сообщения. Автомобильные дорогие обеспечивают необходимые связи внутри городов и между ними. Ежедневно люди пользуются транспортными средствами, личными или общественными.
За последние 20 лет уровень автомобилизации (исходит из количества транспортных средств на 1000 человек) увеличился в три раза. График роста автомобилизации изображен на рисунке 1.
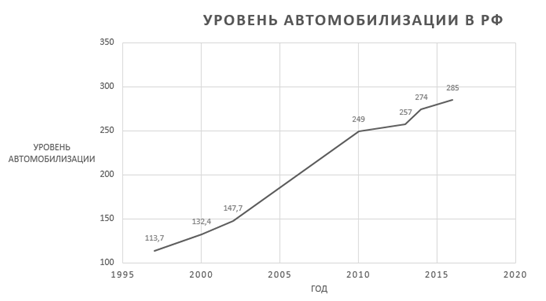
Рисунок 1 – График роста уровня автомобилизации в РФ.
Многие города, а точнее автомобильные дороги в них, не были готовы к такому росту числа автомобилей. Вследствие чего увеличилось количество заторов на дорогах. В основном заторы возникают на перекрестках, так как их пропускной способности часто не хватает. Автомобили скапливаются перед красным сигналом светофора и образуется чередь, которая может тянуться до предыдущего перекрестка. В такой очереди водителям приходиться довольно часто передвигаться короткими дистанциями стартуя и сразу же останавливая автомобиль. Это наносит сильный удар по нервам, но и не менее сильный по экологии, ведь за расстояние, которое автомобиль проезжает режиме очереди он выделяет намного больше выхлопных газов, чем за такое же расстояние, преодоленное на нормальной скорости.
У этой проблемы есть несколько решений. Либо полная перепроектировка большого участка дороги, либо внедрение информационной системы управления транспортным потоком, при помощи которой можно будет повысить пропускную способность перекрестка и уменьшить время простоя автомобилей.
Перепроектировка довольно затратный процесс и не всегда возможен. Более целесообразное решение – это информационная система. С её помощью можно будет управлять работой светофоров на перекрестке так, что менять длительность фаз светофора в зависимости от загруженности улиц. К примеру, если на одной из улиц перекрестка слабый поток автомобилей, а ну другой наоборот, то для второй улицы зеленый сигнал будет длиться дольше. Аналогичные системы уже существуют, но в основном они работают только на конкретных участках дорог. Поэтому возникает необходимость создания собственной системы для оптимизации автомобильного трафика на перекрестках.
Постановка задачи
Рассмотрим задачу создания системы оптимизации автомобильного трафика на перекрестках. Критерием оптимизации транспортного потока на перекрестке является сведение к минимуму общей задержки транспортных средств на перекрестке.

где T – промежуток времени, на котором будет проводиться оптимизация, N – количество машин, которые пересекают перекресток, на промежутке времени Т, Di – время простоя автомобиля перед светофором, – средняя задержка на перекрестке, на промежутке времени T.
Перед тем как разрабатывать информационную систему с каким-либо методом оптимизации, нужно убедиться в адекватности метода перед внедрением. Для этого нужно использовать имитационную модель, в ходе работы которой можно будет увидеть влияние метода оптимизации на транспортный поток.
Имитационное моделирование как метод исследования подобных объектов представляется обещающим подходом к решению этой проблемы. Оно позволяет быстро и с хорошей точностью прогнозировать характеристики сложных систем подобной природы и оптимизировать существенные параметры, выбирая соответствующие параметры оптимизации. К сожалению, адекватность таких моделей сложно оценить, так как это требует больших ресурсов, чтобы сопоставить результаты роботы модели и реальное поведение транспортного потока. Очень сложно идеально повторить все входящие параметры модели в реальных условиях.
Для разработки требуемой системы проведем анализ существующих методов моделирования автомобильного трафика и выделим наиболее подходящий для моделирования работы перекрестка.
Анализ существующих методов моделирования транспортных потоков
Модели, применяемые для анализа транспортного потока довольно разнообразны, но при этом на данный момент не существует их исчерпывающей классификации. Можно попробовать разделить в зависимости от решаемых задач. Например, от метода решения – на аналитические и имитационные [1,2] по методам представления данных – на динамические (в реальном времени) и статические, в которых параметры задаются на определенный интервал времени [4]. Так же по временной шкале – дискретные и непрерывные [5]. В зависимости от типа представления процесса модели – стохастические и детерминированные [3]. Основываясь на функциональной роли модели, можно выделить в основном три типа [5]:
- Прогнозныее модели
- Оптимизационные модели
- Имитационные модели
Но наиболее популярной является классификация по уровню детализации транспортного потока [6]. В ней выделяют макроскопические, мезоскопические, микроскопически и субмикроскопические модели. Однако, такая классификация не дает представления ни о методе моделирования, ни об области применения.
Рассмотрим классификацию по уровню детализации и методу моделирования, которая приведена ниже в таблице.
Таблица 1. Классификация моделей по уровню детализации и методу моделирования

Макроскопический уровень детализации рассматривает транспортный поток как жидкость. При таком моделировании можно изучить усредненные характеристики потока. Например, плотность, среднюю скорость, интенсивность, но транспортные средства как отдельные единицы не рассматриваются. Такие модели могут быть непрерывными, описанными дифференциальными уравнениями в частных производных, либо дискретными.
Модель Лайтхилла-Уизема-Ричардса(LWR) [7] отражает основные характеристики макроскопического подхода. Данная модель относиться к моделям-аналогам, основана на уравнениях гидродинамики и выполнении закона сохранения массы, под массой подразумевается количество автомобилей. Но эта модель не работает при очень низких и очень высоких плотностях транспортного потока, неадекватна вблизи «узких мест» и перекрестков со светофорами, поэтому такая модель не подходит для нашей задачи.
Макроскопические модели обычно применяются для определения времени движения, средней скорости, уровня нагрузки сети, интенсивности движения. Однако полученные результаты являются статичными и недостаточно точными.
Мезомоделирование описывает транспортные средства достаточно точно, но рассматривает их поведение и взаимодействие так же, как и на макроуровне.
Гравитационная модель отображает взаимодействие нескольких районов, которые порождают транспортные потоки (корреспонденции). В её основе лежит закон всемирного тяготения. В модели равновесного распределения предполагается, что участники движения выбирают свой путь опираясь на минимальную цену поездки. В результате процесса «проб и ошибок» в системе устанавливается равновесие, обладающее свойствами, известными как требования Вардрупа [9].
Основным достоинством данных моделей является их компактность. Однако, эти модели охватывают лишь ограниченный набор параметров, слабо учитывают динамику транспортного потока
В микроскопических моделях детально рассматривается каждая машина. Микромодели обрели популярность после появления мощных вычислительных компьютеров, так как они требуют большого количества расчетов. Такая степень детализации хорошо подходит для представления движения по дороге с несколькими полосами, потому что могут описать реалистичные правила движения для каждого автомобиля.
Одной из первых таких моделей, была модель «следования за лидером» [10]. Основная идея заключена во влияние ведущего автомобиля на следующие за ним машины. Данная теория довольно долго разрабатывалась и подвергалась изменениям, в частности стали учитывать время реакции водителей, изучали устойчивость, исследовали движение на многополосных дорогах. Со временем была выдвинута более продвинутая модель «разумного водителя» [8]. В этой модели движение описывается как сочетания двух стратегий: торможения и ускорения. В зависимости от расстояния до впереди идущего автомобиля выбиралась одна из стратегий. Такая модель учитывает психофизические параметры людей, что помогает более реалистично моделировать транспортные потоки.
Модели, основанные на следовании за лидером, некорректно описывают динамику отдельного транспортного средства, что позволяет отнести их к мезоскопическим моделям. Так же в них есть парадокс – если нету лидера, то ускорение становиться равным нулю.
Более подходящими аппаратом для реализации микроскопических моделей являются клеточные автоматы [11]. В таких моделях дорога разбивается на клетки, время считается дискретным. У каждой ячейки может быть состояние, которое определяется набором правил, зависящих от состояния соседних ячеек. В статье [12] была описана такая модель, и на её основании были найдены такие сочетания фаз светофоров, при которых задержки транспорта были минимальными. Результаты данных исследований приведены ниже.
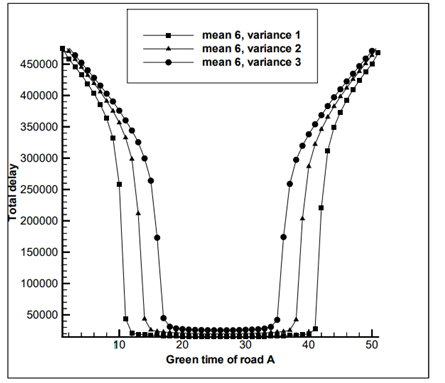
Рисунок 2 – Результаты работы модели на клеточных автоматах, для расчета задержки автомобилей при различных фазах светофора
Такая модель является лучшим выбором, для решения поставленной задачи, так как с её помощью можно с высокой степенью детализации смоделировать поведение транспортных средств на регулируемом перекрестке и отработать на неё оптимизационный метод. Достоинством такой модели является высокая эффективность при компьютерном моделировании.
Основным преимуществом микроскопических моделей является возможность получения оценок с высокой точностью. Однако требуется много ресурсов для сбора исходных данных, необходима калибровка параметров, высокая чувствительность к ошибкам в исходных данных. Как правило, результатами работы микроскопических моделей являются такие данные, как длина очереди, время задержки транспортных средств, средняя скорость, максимальная или минимальная скорость, время движения автомобилей. Эти данные соответствуют нашей поставленной задаче.
Заключение
Были проведены анализ и классификация существующих моделей имитации транспортных потоков. Выбран метод моделирования на основе клеточных автоматов с микроскопическим уровнем детализации. В дальнейшем будет разработана собственная система оптимизации автомобильного трафика, основана на выбранном методе моделирования.
Список источников
- Гасанов, Г.М. Управление транспортно-эксплуатационным состоянием автомобильных дорог. – М.: МАДИ (ГТУ), 2004. – 172 с
- Кисляков В.М. Математическое моделирование и оценка условий движения автомобилей и пешеходов / В.М. Кисляков, В.В. Филиппов, И.А. Школяренко. – М.: Транспорт, 1979. – 200 с.
- Семенов В.В. Математическое моделирование транспортных потоков мегаполиса. M.: препринт № 34 Инст. Прикл. математики им. М.В. Келдыша РАН, 2004. – 44 c
- Швецов В.И. Математическое моделирование транспортных потоков // Автоматика и Телемеханика. – 2003. – № 11. – С. 3–46
- Gazis D.C., Herman R., Potts R. B. Car-Following Theory of Steady-State Traffic Flow // Operations Research. – 1959. – Vol. 7, № 4. – P. 499–505
- Savrasov M. Development of new approach for simulation and analysis of traffic flows on mesoscopic level: doctoral thesis. – Riga, 2013. – 161 p.
- Ligthill M.J., Whitham F.R.S. On kinetic waves II. A theory of traffi c fl ow on crowded roads // Proc.of the Royal Society Ser.A. – 1995. – Vol. 229. – № 1178. – P. 317–345.
- Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Н.Б. Введение в математическое моделирование транспортных потоков: учеб. пособие / ред. Гасникова А.В. – М.: МФТИ, 2010. – 362 с
- Wardrop J.G. Some theoretical aspects of road traffic research // Proc. Institution of Civil Engineers II. – 1952. – Vol. 1. – P. 325–378
- Буслаев А.П., Новиков А.В., Приходько В.М., Таташев А.Г., Яшина М.В. Вероятностные и имитационные подходы к оптимизации автодорожного движения. – М.: Мир, 2003. – 368 с
- Куржанский А.А., Куржанский А.Б., Варайя П. Роль макромоделирования в активном управлении транспортной сетью // Труды МФТИ.– 2010. – № 4. – С. 100–118
- M. Ebrahim Fouladvand, Nima Hamedani Radja Optimized Traffic Flow at a Single Urban Crossroads : Dynamical Symmetry Breaking //arxiv.org/abs/cond-mat/0108149