Аннотация
Рассматривается вопрос определения управляющих парамет-ров модели управления транспортными потоками на улично-дорожной сети города.
Ключевые слова:
система управления дорожным движением, улично-дорожная сеть, магистраль, транспортный поток, имитационная модель, оптимизация.
Введение
Высокая степень автомобилизации и возрастающая роль дорожного движения делают проблемы управления особенно актуальными.
Возрастающие скопления транспортных средств на улично-дорожной сети городов не только повышают затраты за счет непродуктивных потерь времени, но также увеличивают вероятность происшествий и оказывают негативное влияние на окружающую среду и качество жизни людей.
Решение подобных проблем невозможно без математического моделирования, главной задачей которого является определение параметров функционирования транспортных сетей – скорости движения транспортных средств, величины транспортной задержки, потери времени участников транспортного процесса в пути следования и оценки пропускной способности улично-дорожной сети.
Цель и постановка задачи
Основываясь на функциональном назначении моделей, можно условно выделить три основных класса моделей [1]:
- прогнозные модели;
- имитационные модели;
- оптимизационные модели.
При этом основными требованиями являются эффективность их применения и точность математического описания объекта.
С помощью моделей прогноза можно оценить предполагаемые изменения параметров транспортного потока и транспортной сети.
В отличие от них имитационное моделирование позволяет воспроизводить особенности движения как индивидуальных транспортных средств, так и транспортного потока в целом. Одним из требований к имитационным моделям является скорость выполнения моделирования. Поэтому при выборе стратегии локального управления транспортным потоком (ТП) преимущество имеют более точные, но «медленные» модели, в то время как для системного управления ТП в реальном времени быстродействие модели является одним из важнейших параметров системы управления.
В настоящее время актуальной задачей является разработка систем управления дорожным движением, работающих в режиме реального времени [1].
Такие системы предполагают применение информации от первичных измерительных устройств (детекторов транспорта) в сочетании с динамическим имитационным моделированием. Такой класс моделей предполагает решение оптимизационных задач функционирования транспортных сетей, при этом выбор методов оптимизации представляет собой определенную область исследований.
Таким образом, целью статьи является разработка имитационной модели управления транспортными потоками на уличнодорожной сети города.
Проведенные исследования транспортной системы методами системного анализа позволили выявить, что одной из наиболее значимых задач при достижении генеральной цели – повышение безопасности участников транспортного процесса – является усовершенствование методов управления транспортными потоками.
Для этого нами была использована SADT (Structured Analysis and Design Technique) – методология структурного анализа и проектирования, что позволяет описывать системы, обладающие повышенной сложностью. Известны локальные, системные и магистральные методы управления дорожным движением.
Объектом исследования данной статьи является магистральный метод управления дорожным движением, который относится к наиболее перспективным методам управления ТП в городах.
Решение задачи
При магистральном управлении движением рассчитывают сдвиги фаз светофорного регулирования на пересечении магистрали (?), а также ширину ленты времени, которая называется временем безостановочного движения (tл).
Разработанная имитационная модель координации светофорного регулирования на уличнодорожной сети (УДС) города предназначена для воспроизведения динамики дорожного движения по транспортной сети города с целью выравнивания скоростью движения транспортного потока по прямолинейным участкам [2]. Фрагмент транспортной сети, для описания которой предложена имитационная модель, приведен на рис. 1.
Задачей управления дорожным движением в этом случае является выравнивание скорости по пересекающимся элементам УДС с расчетом управляющих параметров светофорного регулирования на всех перекрестках транспортной сети.
Блок-схема имитационной модели приведена на рис. 2.
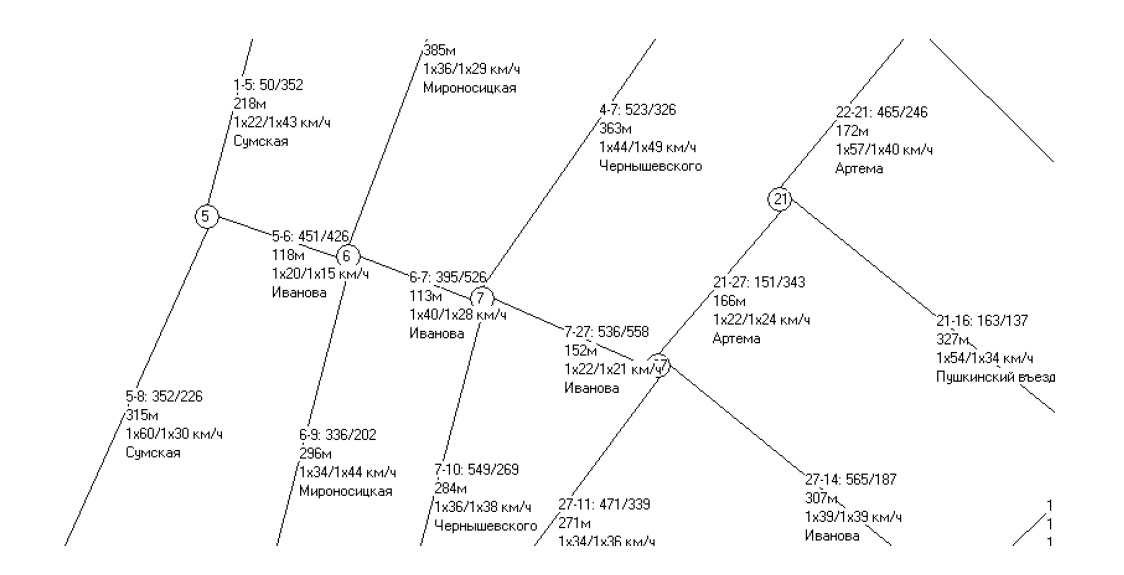
Рис. 1. Схема транспортной сети
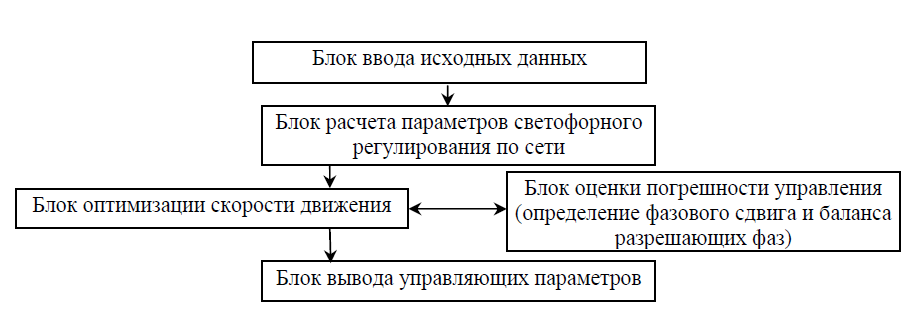
Рис. 2. Блок-схема имитационной модели управления транспортными потоками
Исходные данные представлены в следующем виде:
n– количество перекрестков; m – количество перегонов; Xk, Yk – координаты k-го перекрестка на плоскости, k=1...n; LEWk, LNSk – линейные размеры перекрестка по горизонтали (с востока на запад) и вертикали (с севера на юг); N– интенсивность транспортных потоков на подходах к перекрестку; CHj, CKj – индекс начала и окончания j-го перегона, j=1...n; ? – коэффициент кривизны перегона; LCH-CK, LCK-CH – количество полос движения на перегоне в обоих направлениях; Vb CH-CK, Vb CK-CH – базовые скорости движения транспортных средств на перегоне.
Матрица распределения интенсивности ТП для перекрестков
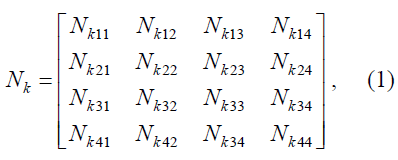
где Nkij – интенсивность потока, движущегося на k-м перекрестке от въезда i к въезду j; k=1...n, i, j=1...4.
Критерием оптимизации является минимизация суммы квадратов отклонений текущей расчетной скорости от эталонного значения (в начале) или от скорости движения на смежном перегоне


где a1 – признак наличия условия равенства скорости в направлении CH-CK – заданной величины; a2 – признак наличия условия равенства скорости в направлении CK-CH – заданной величины; a3 – признак наличия условия равенства скоростей с другим перегоном.
Размерность задачи оптимизации

где gmax – количество перекрестков, минимальный цикл которых равен общему для всех перекрестков.
При решении оптимизационной задачи нами был реализован метод комплекса. Для сложных «овражных» функций из всей череды известных методов оптимизации ни один, основанный на исследовании ближайших к исходной точек и постепенном перемещении в сторону увеличения критерия или уменьшения значения функции (методы прямого поиска – Нелдера-Мида, Хука-Дживса, Спендли-Хекста-Химсворта, Розенброка, Пауэлла, первого порядка – градиентный, метод Коши, второго порядка – Ньютона), не подходит. Метод постепенно приближается к ближайшему локальному экстремуму функции и не покидает этот участок, хотя в отдаленном месте может быть более выгодное положение. Для перехода на более выгодный участок необходимо более обширное исследование области достигнутого локального экстремума, что не присуще перечисленным известным методам оптимизации.
Единственным методом, исследующим обширную область точек, является так называемый «метод комплекса» [3]. Вывод результатов расчета производится в следующем формате (рис. 3).

Рис. 3. Структура выходных параметров модели
Адекватность модели была проверена на участке транспортной сети центральной части города Харькова и дала положительные результаты.
Выводы
Предложенная имитационная модель управления транспортными потоками в городах реализует усовершенствованный метод координированного управления транспортными потоками на отдельных магистралях города. При этом предложено введение нового управляющего параметра – баланс разрешающих фаз светофорного регулирования, под которым мы понимаем разницу между значениями максимального цикла светофорного регулирования по сети и циклом светофорного регулирования в локальном режиме на определенном перекрестке.
Список источников
- Григоров М.А. и др. Проблеми моделювання і управління рухом транспортних потоків у великих містах: Монографія. – Одеса: Астропринт, 2004. – 272 с.
- Абрамова Л.С., Чернобаев Н.С. Постановка задачи оптимизации адаптивного управления дорожным движением // Ві-сник ДІАТ. – Донецьк: Вид-во ПП Рекламно-виробнича фірма «Молнія» – 2009. – №1. – С. 7 – 12.
- Методы робастного, нейро-нечеткого и адаптивного управления: Учебник / Под ред. Егупова Н.Д. – М.: МГТУ им. Н.Э. Бау-мана, 2002. – 744 с.