Аннотация
Освещается опыт применения метода обобщенных переменных и теории размерностей в количественной оценке различных условий движения транспортных потоков с учетом уровня загрузки дороги.
Ключевые слова:
количественные соотношения, комплексные и параметрические критерии, матрицы, скорость, плотность, интенсивность, динамический габарит.
Введение
Эффективное применение положений теории состояний транспортного потока в практических целях становится возможным только в том случае, когда теоретические представления приобретают конкретный и точный характер в количественной форме. При этом полнота количественной информации, достаточной для технических приложений, будет достигнута, когда каждая из величин, существенных для транспортного процесса, будет определена как функция аргументов, характеризующих движение транспортного потока. В подавляющем большинстве случаев попытка на практике найти аналитическое решение в задачах организации движения и проектирования дорог и улиц наталкивается на значительные, а иногда и непреодолимые трудности, вызванные сложностью транспортного процесса и громоздкостью математического аппарата. Поэтому нередко получаются результаты, которые в лучшем случае имеют характер приближенной оценки, в худшем – неправильны по существу и поэтому являются причиной глубоких заблуждений. Разрозненные частные экспериментальные зависимости, связывающие друг с другом отдельные переменные, не объединены общим уравнением и не могут привести к полной и отчетливой картине.
Анализ публикаций
Опыт применения данного метода для оценки состояний транспортного потока в публикациях не отражен.
Цель и постановка задачи
Численные методы могут быть существенно усилены с помощью других средств исследования, основанных на анализе физического механизма транспортного потока и приводящих к важным соотношениям, которые не удается получить другими способами. Как показывает опыт, синтез этих соотношений и данных численного решения или эксперимента оказывается чрезвычайно плодотворным [1–3]. Для определения количественных соотношений заменим обычные переменные транспортного потока величинами комплексного типа, которые составлены из тех же переменных, но в определенных сочетаниях, зависящих от природы транспортного потока. Комплексные переменные, согласно [1–2], являются обобщенными переменными и определяются на основе теории размерностей или метода обобщенного анализа.
Решение задачи
Критерии параметрического типа представляют собой простые отношения одноименных параметров; критерии комплексного типа объединяют в себе разнородные параметры. Относительные переменные представляют собой частные от деления переменных на постоянные параметры. На указанной основе определим обобщенные критерии Пн , которые в дальнейшем используем и в качестве параметров, и в качестве переменных транспортного потока, представив их произведением различных степеней безразмерных величин. При этом в качестве основных единиц измерения транспортного потока примем фундаментальные измерители:
- автомобиль [А], чем обобщаются его геомет-рические и динамические параметры;
- протяженность [L] (м, км) дороги, автомоби-ля, динамического габарита, поперечного сечения дороги и т.д.;
- время [T], (с, ч).
Размерность любой величины выразится через основные единицы измерения, т.е.
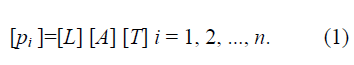
Чем меньше число параметров, определяющих изучаемую величину в транспортном потоке, тем больше ограничена форма функциональной зависимости и, следовательно, тем проще будет вести исследование.
Рассмотрен ряд задач транспортного потока в целях установления обобщенных критериев, характеризующих состояние транспортного процесса. Как указывалось выше, для решения транспортных задач в количественной форме необходимо последовательное применение безразмерных величин, т.е. критериев подобия и относительных переменных. При этом «решение задачи представляется в форме уравнений в безразмерных величинах, которыми искомые относительные переменные определяются как однозначные функции независимых относительных переменных и критериев подобия, играющих роль постоянных параметров» [1, с. 54]. Следовательно, общий тип уравнения будет иметь вид
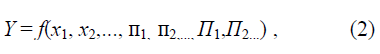
где Y – искомая переменная транспортного потока; х – независимая переменная; п – критерии комплексного типа; П – критерии параметрического типа.
Вид функции (2) в конечном выражении не определяется. Наибольшая полнота знаний о процессе движения транспортного потока при количественном исследовании будет достигнута, когда будут найдены распределения переменных в пространстве и во времени. Совокупность мгновенных значений, непрерывно распределенных в пространстве, в физике принято называть полем [1].
Рассмотрим ряд последовательно усложняющихся задач процесса движения автомобилей в транспортном потоке и самого потока. Выявим вначале процесс изменения динамического габарита (соответственно и дистанции) автомобиля в транспортном потоке из-за близости автомобилей на пространственной оси проезжей части. Размеры динамического габарита S определим следующими величинами: V – скоростью автомобиля, км/ч; м/сек; Q – плотностью потока, авт/км; авт/м; х – протяженностью участка полосы движения, км; м; а – ускорением автомобиля, км/ч; м/сек ; N – интенсивностью потока, авт/ч; авт/сек, или
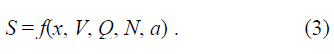
Вполне понятно, что аналитически получение вида зависимости (3) затруднительно, экспериментальное определение чрезвычайно трудоемко, т.к. требуется определить связь между шестью величинами. Однако, перейдя к критериям, вместо к = 6 величин получим n – m = 6 – 3 = 3 критерия. Найти связь между тремя величинами значительно легче. Примем в качестве основных независимых переменных x, V, а. Найдем искомые критерии:
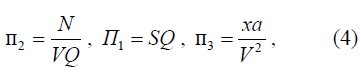
откуда для динамического габарита можно записать
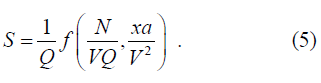
Проанализируем полученные критерии (5) при условии, когда они постоянны.
Из первого критерия П1 видно, что динамический габарит автомобилей в потоке зависит обратно пропорционально только от плотности транспортного потока Q (S = Q-1). Это критерий параметрического типа, он широко применяется в прикладных расчетах. Второй критерий – п2 указывает, что увеличить размеры интенсивности N транспортного потока на участке полосы движения возможно только или с уменьшением скорости потока V, или с уменьшением расстояния между автомобилями, т.е. увеличив плотность потока. Критерий п2 характеризует меру отношения между интенсивностью потока и пропускной возможностью участка. В практических расчетах этот критерий как отношение N/Nmax применяется для оценки уровня загрузки дороги и уровня удобства движения. Поэтому критерий п2 является обобщенным критерием для оценки транспортного процесса и учитывает влияние состояния дорог на уменьшение скорости движения. В транспортной теории соотношение п2 известно как уравнение состояния потока. Критерий п3 характеризует относительную (в сопоставлении с инерционными) величину динамических возможностей автомобиля, и поэтому он является существенным, когда автомобиль двигается в потоке с частыми обгонами и резкими ускорениями. Им учитывается шум ускорений.
Из требования постоянства критерия п3 следует, что скоростные возможности автомобиля xa должны быть больше скорости транспортного потока Vі . Критерий п3 учитывает влияние транс-портного потока на скорость движения автомобиля в потоке и, кроме того, он указывает, что количественное значение скорости транспортного потока существенно зависит от длины участка, на котором эта скорость определяется, что не всегда учитывается в экспериментальных наблюдениях.
Рассмотрим теперь процесс движения транспортного потока через сечение дороги и линию «стоп». Параметрами и переменными транспортного потока при движении через сечение дороги будут следующие: N – интенсивность, авт/час; B – ширина проезжей части в сечении, м; b – ширина полосы движения, м; Q – плотность потока, авт/км; V – скорость движения, км/ч.
Изменение интенсивности транспортного потока есть функция

Примем за основные единицы B, V, Q, где критерии

В рассматриваемом случае критерий подобия п1 определен нами ранее. О его общности также упоминалось. Критерий подобия П4 характеризует использование проезжей части транспортным потоком по ширине дороги и является, при по-тоянных размерах полосы движения и ширины проезжей части, параметрическим числом. Для полосы движения шириной 3,5 м П4 находится в пределах 0,714–0,73, для полосы в 3,75 м – 0,68–0,594.
Для более полной характеристики состояния движения транспортного потока определим возможные критерии при оценке условий движения в пространстве и во времени. Будем характеризовать транспортный поток всеми полученными выше параметрами и переменными. Такой подход позволит получить наибольшую разновидность количественных соотношений. Учтем:
- протяженность полосы движения x, км; [L];
- время движения Т, час; [Т];
- скорость потока V км/ч; [L][T]-1;
- плотность потока Q, авт/км; [A][L]-1;
- количество потока q , авт; [А];
- интенсивность N , авт/ч; [А][T]-1,
- мощность потока М, авт.км/ч; [А][T-2][L];
- количество движения Д, авт.км; [А][L];
- работу потока Н, авт.км/ч; [А][L][Т]-1;
- динамический габарит S, км/авт, [L][А]-1;
- инерционность потока J, авт.ч/км, [A][T]]L]-1;
- напряженность движения С, км.ч/авт, [L][Т][А]-1;
- габаритная длина автомобиля la, м [L];
- ускорение автомобиля а м/с, [L][Т]-2.
Теперь интенсивность транспортного потока на одной полосе определим как функцию указанных выше величин:

Из указанных 14 величин получим n – m различных критериев. Так как m = 3, то критериев будет 14 – 3 = 11. B качестве основных единиц принимаем протяженность x, скорость V и количество потока q. Обобщая, найдем интенсивность в пространственном представлении:

Во временном представлении вместо базового параметра x необходимо принять время Т, поэтому ряд критериев изменится. Тогда

Как видно из уравнений (9) и (10), все отношения, стоящие в правой части, представляют собой комплексные и параметрические критерии.
Выводы
Несомненный научный и практический интерес имеет сам анализ полученных количественных соотношений, т.к. появляется возможность рассматривать с количественной стороны условия движения транспортного потока на различных участках улиц и дорог с учетом одновременного влияния многих факторов.
Полученные количественные соотношения более полно, чем коэффициенты загрузки, ускорения и замедления движения, определяемые как отношения текущих значений интенсивности, скорости и плотности к их максимальным значениям [4], позволяют оценить качество и состояние условий движения в транспортном потоке, т.е. уровни удобств движения и управлять его качеством в автоматизированных системах типа АСУД.
Список источников
- Веников В.Л. Теория подобия и моделирование (применительно к задачам электроэнергети-ки): Учеб. пособ. для вузов. – М.: Высшая школа, 1976. – 479 с.
- Седов Л.И. Методы подобия и размерности в механике. – М.: Наука, 1972. – 440 с.
- Гук В.И. Элементы теории транспортных пото-ков и проектирования городских улиц и до-рог: Учеб. пособие. – К.: УМК ВО, 1991. –256 с.
- Highway capacity manual. Trb. HCM, 2000.