Аннотация
Дашкевич Д.О., Секирин А.И. – Моделирование системы массового обслуживания перевозки пассажиров Рассмотрены различные методы моделирования систем массового обслуживания с учетом особенностей поставленной задачи. Проанализированы реализации данных методов. Определены средства для создания модели.
Актуальность проблемы
За последнее время в самых разных областях практики возникла необходимость в решении различных вероятностных задач, связанных с работой так называемых систем массового обслуживания (СМО). Примерами таких систем могут служить: перевозка пассажиров, ремонтные мастерские, билетные кассы, стоянки такси, парикмахерские и т.п.
В связи с большим пассажиропотоком появляется проблема расчета оптимального расписания движения транспорта по маршруту, чтобы ее устранить предлагается смоделировать перевозку пассажиров.
Анализ существующих методов моделирования СМО
В теории массового обслуживания изучаются системы, на вход которых поступает случайный поток заявок (требований), приходящихся в общем случае на случайные моменты времени. Поступившая заявка обслуживается в системе путем предоставления ей некоторых ресурсов на какое-то время и, будучи в той или иной мере обслуженной, покидает систему. Наиболее характерный момент функционирования систем массового обслуживания – это наличие очередей, в которых заявки ждут момента освобождения ресурсов, занятых обслуживанием других заявок. В простейшем случае система массового обслуживания определяется потоком заявок, длиной очереди и дисциплиной обслуживания (порядком выбора заявок из очереди), числом каналов (приборов) обслуживания, распределением длительности обслуживания. В более сложных случаях рассматривается надежность приборов обслуживания.
Существующие методы моделирования СМО можно разделить по нескольким критериям:
- по структуре:
-
одноканальные
Одноканальной называется система, у которой одна очередь, а так же канал для обслуживания только один, следовательно подходит, только если для перевозки пассажиров используется одна единица транспорта.
-
многоканальные
Многоканальной называется система, у которой одна общая очередь, а каналов для обслуживания несколько, следовательно данный тип модели наиболее подходящий для реализации, т к единиц техники обслуживающих пассажиров в большинстве случаев больше одной. Если будет использоваться только одна единица транспорта, то достаточно задать нужные параметры модели.
-
многофазные
Cистема, в которой каналы обслуживания расположены последовательно и выполняют различные операции обслуживания. Не подходит для реализации модели, т к заявки обрабатываются только один раз на одном из каналов.
-
однофазные
Однородные системы, которые выполняют одну и ту же операцию обслуживания, данный тип наиболее подходит для реализации СМО, т к модель выполняет одну и ту же операции, т е перевозку пассажиров.
-
замкнутые.
Система массового обслуживания, в которой обслуженные требования могут возвращаться в систему и вновь поступать на обслуживание.
-
разомкнутые;
СМО в которых характеристики потока заявок не зависят от того, в каком состоянии сама СМО.
-
одноканальные
- по допустимому времени ожидания заявок в очереди:
- система без отказов;
- система с ограниченным ожиданием;
- система без ожидания.
Допускается использование всех типов заявок в очереди, но следует реализовать передачу параметров модели, чтобы указать, какие типы заявок можно использовать, а какие нет.
- по дисциплине выбора очереди:
- заявки выбираются из очереди в порядке поступления;
Параметры заявок, стоящих в очереди сдвигаются следующим образом:
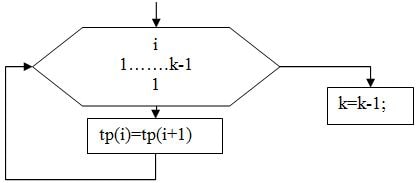
Рисунок 1. Выбор заявки в порядке поступления.
-
заявки выбираются из очереди в случайном порядке;
Если все заявки равноправны, то вероятность выбора любой из них будет равна 1/к. Сам выбор – это моделирование полной группы событий.
Удаление параметров заявки из очереди может осуществляться как во втором случае, а может как в основном алгоритме.
-
заявки выбираются по минимальному времени ожидания;
Необходимо при постановке заявки в очередь запомнить момент возможного отказа, а при выборе заявки из очереди найти соответствующий момент с минимальным значением. Удаление заявки и сдвиг параметров осуществляется аналогично предыдущему пункту, но цикл начинается с номера выбранной заявки.
-
выбор по приоритету.
При постановке заявки в очередь необходимо по заданному в условии правилу сформировать приоритет поступившей заявки и запомнить его. При выборе заявки просматривается массив приоритетов и выбирается заявка с наибольшим приоритетом. Удаление параметров заявки из очереди осуществляется как во втором случае.
Допускается использование всех методов выбора заявки из очереди, но реализовать передачу модели параметров, с указанием какой тип выбора можно использовать, а какой нет, т к в некоторых ситуациях можно использовать только один тип, но иногда несколько, т е комбинировать их.
- заявки выбираются из очереди в порядке поступления;
- по способу выбора канала:
- по минимальному времени освобождения;
- в случайном порядке;
- по приоритету.
Для реализации модели СМО перевозки пассажиров больше всего подходит способ выбора канала по приоритету.
Математическая постановка задачи
Таблица 1. Описание СМО
| СМО | Заявки | Каналы |
| Перевозка пассажиров | Пассажиры | Транспорт (автобусы) |
При моделировании СМО перевозки пассажиров можно организовать алгоритм, укрупнённый вид которого представлен ниже.
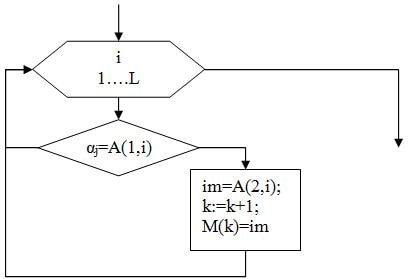
Рисунок 2. Блок-схема алгоритма.
Модель должна принимать такие параметры:
- типы заявок в очереди, которые можно использовать и их параметры.
- дисциплины выбора заявок из очереди, которые можно использовать и их параметры.
- максимальное кол-во транспорта, которое может двигаться по заданному маршруту.
- пассажиропоток на данном маршруте.
Модель СМО разрабатывается и реализуется с целью оценить определенные показатели качества, они являются выходными значениями модели.
Выходные значения модели следующие:
- общее количество обслуженных заявок, за какой-либо промежуток времени;
- пропускная способность – среднее число заявок, обслуженных в единицу времени;
- доля обслуженных заявок;
- доля заявок, получивших отказ, в случае, если данный тип заявок использовался;
- время пребывания заявки в системе (от момента поступления заявки в систему до момента завершения ее обслуживания);
- среднее время обслуживания (функция распределения времени обслуживания);
- средняя длина очереди;
- среднее время ожидания;
- загрузка каналов или коэффициент использования каналов.
Системы массового обслуживания с неоднородными потоками и специализированными каналами
Неоднородный поток в общем смысле характеризуется тем, что имеет совместную, т. е. многошаговую функцию распределения плотности вероятности. Промоделировать такой поток достаточно сложно, поэтому находят способы упрощения описания такого потока. Например, рассматривают моменты поступления заявок, как однородный поток, а после получения момента поступления заявку относят к тому или иному классу и определяют его параметры. Возможен другой подход: разные типы заявок рассматривают как отдельные независимые потоки. Для каждого из типов определяется очерёдной момент поступления заявки, а в системе отправляется на обследование та заявка, у которой минимальный момент поступления.
Для моделирования неоднородных потоков системы можно разделить на три класса.
- Cистема имеет один или несколько каналов, и на всех каналах можно обследовать любой тип заявки. Моделирование таких систем не вызывает трудностей и выполняется как одно или многоканальной системы с учётом разных параметров обслуживаемой заявки;
- У системы для каждого типа заявки имеется отдельный канал (один или несколько). Моделирование таких систем выполняется так же, как и для однородных потоков, но во-первых, необходимо предусмотреть разделитель заявок в соответствии с типами и предусмотреть то, что эти заявки могут обследоваться как каждая в своём канале;
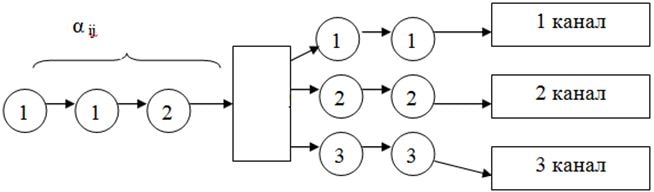
Рисунок 3. У каждой заявки отдельный канал.
- Системы, в которых типы заявок и номера каналов переплелись.
При моделировании таких систем необходимо предусмотреть распределение потоков заявок по соответствующим каналам.
Один из вариантов распределения этих потоков предусматривает создание массива соответствующих параметров.

Рисунок 4. Типы заявок и номера каналов переплелись.
При реализации СМО перевозки пассажиров наиболее подходящим классом является второй, т е когда для каждого типа заявки имеется отдельный канал.
Экспериментальные исследования
Модель была протестирована с использованием наиболее простых параметров и показала хороший результат с достаточно долей соответствия реальным данным о перевозке пассажиров. При моделировании более сложных ситуаций возникают проблемы с подбором параметров модели.
Заключение
Был проведен обзор различных типов СМО. Основными недостатками большинства типов является:
- Ограничение алгоритма модели приводившее к неполному моделированию перевозки пассажиров.
- Невозможность моделировать поставленную задачу.
Алгоритм с неоднородными потоками и специализированными каналами лишен этих недостатков, но обладает трудностью подбора параметров, чтобы модель соответствовала реальным данным.
Для решения данной проблемы возможно использование генетических алгоритмов при подборе параметров модели, но это увеличивает затрачиваемые ресурсы при моделировании, т. к. подбор параметров напрямую зависит от мощности аппаратной части и оптимизации алгоритма, то это может занять длительный промежуток времени.
В настоящее время имеется несколько реализаций этого метода, однако, программное обеспечение включает в себя множество методов моделирования из-за чего возрастает стоимость, либо программное обеспечение невозможно приспособить к решению данной задачи.
Программа реализована на языке C#. При проведении экспериментов программа показала допустимое отклонение от реальных данных, достаточное для решения поставленной задачи.
Литература
- Светличная В.А. Моделирование систем. [Текст] В.А. Светличная 2009. – 36 c.
- Stratum. Моделируй свою реальность. – 1998–2011. – [Электронный ресурс]. &ndash Режим доступа: http://stratum.ac.ru/textbooks/modelir/lection30.html.
- Элементы теории массового обслуживания. – 1998–2011. [Электронный ресурс]. &ndash Режим доступа: http://edu.dvgups.ru/METDOC/EKMEN/ETR/WEBUMK/frame/4.htm.
- Советов Б.Я.. Яковлев С.А. «Моделирование систем». [Текст] Б.Я. Советов, С.А. Яковлев. Учебное пособие 3-е юд., перераб. и доп. 2001.
- Бусленко Н. П.. Моделирование сложных систем. [Текст] М.: Наука, 1978, 400 с.
- Лоу Аверил М., Кельтн В. Девид «Имитационное моделирование». [Текст] М. Лоу Аверил, В. Девид Кельтн. Питер, Издат.группа BHV 2004 – 848 с.
- Поляк, Ю. Г. Вероятностное моделирование на ЭВМ. [Текст] / Ю.Г. Поляк. – М. : Сов. Радио, 1971. – 400 с.
- Лекции по моделированию систем. – 2009–2011. [Электронный ресурс]. &ndash Режим доступа: http://www.studfiles.ru/dir/cat32/subj1235/file11058/view112484/page1.html.