Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 4 Примеры переброски дуг
- 5 Анализ основных видов конечных автоматов
- 5.1 Детерминированный конечный автомат
- 5.2 Недетерминированный конечный автомат
- 6 Выводы
- Список источников
Введение
Конечный автомат (state machine) – модель, которую удобно использовать в самых различных областях, начиная от моделирования логических устройств в технической диагностике и заканчивая структурированием приложений. В частности, одним из приложений конечных автоматов является моделирование неисправностей дискретных устройств. Часто такие неисправности можно описать как переброску дуг в автомате при сохранении выходных реакций.
Представляют интерес такие переброски, которые изменяют поведения автомата. Известен ряд работ, в которых исследуются свойства перебросок такого рода. В настоящей работе продолжается исследование свойств автоматов, подверженных переброске дуг и наблюдение за дальнейшей его деградацией.
1. Актуальность темы
Модель конечного автомата прошла хорошую проверку временем. Использование конечных автоматов позволяет разработчикам создавать хорошо организованные логические системы с гибкими возможностями, а также анализировать их поведение в различных условиях.
Например, в играх часто используют различные персонажи, которые перемещаются в области игры и могут действовать в различных режимах. Использование конечных автоматов с четко определенными правилами для каждого персонажа, определяющими возможные варианты его поведения в различных состояниях и допустимые переходы из одного состояния в другое, позволяет создавать сложные варианты поведения как персонажей, управляемых компьютером, так и персонажей, управляемых пользователем [1].
Настоящая работа относится к теории экспериментов с автоматами. Экспериментом называют процесс подачи на автомат последовательности входных сигналов, наблюдение соответствующей реакции автомата и вывод заключения о функционировании и свойствах автомата, основанных на этих наблюдениях и априорной информации об автомате. Основная задача теории экспериментов состоит в разработке эффективных экспериментов, позволяющих получить определенные сведения о строении автомата, его функциях, о характеристиках процесса преобразования информации, осуществляемого этим автоматом.
Под экспериментом будем понимать переброску дуг в конечном приведенном автомате. В результате переброски поведение автомата, понимаемое как множество вход-выходных деревьев, порождаемых всеми его состояниями, может только убывать по мощьности.
Пусть А – заданный автомат. Выполним всевозможными способами переброску в нём одной дуги. Каждой переброске соответствует nk –количество состояний, попарно не эквивалентной друг другу в результирующем автомате. Найдем минимум среди всех таких nk. Это число назовем характеристикой деградации поведения исходного автомата при переброске k –дуг. Затем увеличим k на единицу и повторим процесс. Среди всех найденных минимумов найдем минимальное nk (по k). Для нас представляет интерес как изменяется указанная величина nk с ростом числа перебрасываемых дуг k. Это изменение назовем функцией деградации поведения автомата.
Таким образом, исследование функции деградацции поведения конечного автомата является, с одной стороны, продолжением изучения задачи о перебросках, а с другой стороны, является попыткой построить зависимость между числом перебрасываемых дуг и максимальным числом состояний автомата, которые могут оказаться различимыми в результате переброски. В силу сказанного, данная задача является актуальной.
2. Цель и задачи исследования, планируемые результаты
Объектом исследования является поведение конечного при переброске дуг.
Предметом исследования является исследование метода построения функции деградации поведения конечного автомата в результате переброски дуг.
Целью магистерской диссертации является разработка и исследование метода построения функции деградации поведения конечного автомата в результате переброски дуг.
Основные задачи работы:
- провести анализ поведения конечного автомата в результате переброски k –дуг (рис. 1);
- найти минимальное число состояний в автомате, являющемся результатом переброски k –дуг;
- построить функцию деградации поведения автомата с ростом k и разработать метод исследования этой функции.
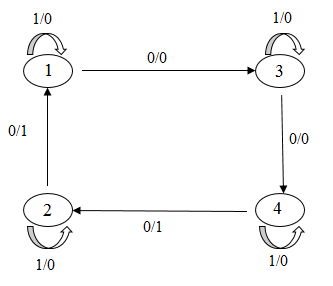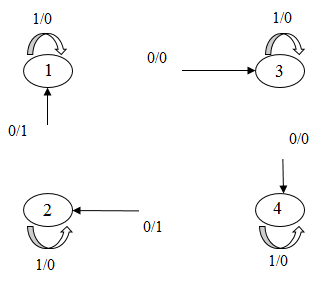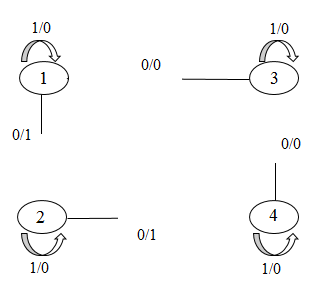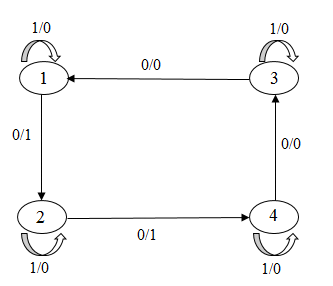
Рисунок 1 – Переброска 4-х дуг в автомате
(анимация: 17 кадров, 3 цикла повторения, 82,1 килобайт)
3. Обзор исследований и разработок
Автоматы, близкие по поведению в том или ином смысле, исследуются достаточно давно, равно, как и структура классов таких автоматов. В основном, эта задача рассматривается в рамках теории экспериментов с автоматами.
Основание теории экспериментов с автоматами было положено Муром. В его работах исследование проводилось в двух направлениях: неотличимость автоматов никаким кратным и никаким простым экспериментом, а также распознавание автомата и его состояний с помощью таких экспериментов. В дальнейшем теория экспериментов получила развитие в работах Ф. Хенни, Мили, Брауэра и других. Методы и результаты анализа автоматов и алгоритмов проведения экспериментов с ними достаточно полно представлены в известной книге А. Гилла.
Отечественные работы в области экспериментов с автоматами связаны с именами A.M. Богомолова и его учеников, М.П. Василевского, В.Н. Носкова, Н.В. Евтушенко, А.Ф. Петренко, И.К. Рысцова, В. А. Твердохлебова, С.В. Яблонского, В.Б.Кудрявцева и др.
Теория экспериментов интенсивно развивается и в настоящее время. В [2-4] получен ряд результатов, связанных с анализом поведения автоматов в условиях воздействия на них факторов внешней среды. В ряде работ изучалось влияние перебросок дуг на поведение автомата. В теории графов также рассматривались родственные задачи, где изучалась задача определения, когда один из графов (автомат) может быть получен из другого в результате некоторой последовательности перебросок дуг.
4. Пример переброски дуги
Напомним, что переброска одной дуги всегда приводит к неизоморфному автомату. Легко привести примеры, когда переброска в автомате двух дуг также порождает новый автомат, не изоморфный исходному.
В [4] были сформулированы достаточные условия сохранения поведения автоматом при переброске двух дуг, и было показано, что для любого натурального k > 1 существует приведенный автомат, в котором найдется подмножество из k дуг, одновременная переброска которых приводит к изоморфному автомату. В [5] было доказано, что при переброске двух дуг вход–выходные отметки на этих дугах совпадают. Там же были приведены примеры не сильно связных автоматов, допускающих переброску нескольких дуг, и было высказано предположение, о том, что состояния, из которых перебрасываются дуги, не достижимы из тех состояний, куда направлена переброска.
Приведем ряд примеров, когда переброска не изменяет поведения исходного автомата.
Граф А (см. рис.2) является результатом переброски двух дуг в графе А: дуга (6, 0, 0, 8) перебрасывается в состояние 9 и заменяется дугой (6, 0, 0, 9), дуга (7, 0, 0, 9) заменяется дугой (7, 0, 0, 8). Нетрудно видеть, отображение ?: А > А, при котором(1) = 1; (2) = 2; (3) = 3; (4) = 4; (5) = 5;(6) = 7; (7) = 6;(8) = 8;(9) = 9, является изоморфизмом графа А на граф А.
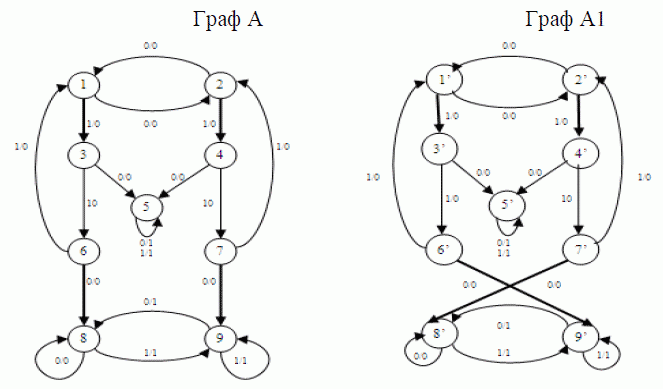
Рисунок – 2. Пример изоморфизма автоматов при переброске двух дуг
В данном примере компоненты сильной связности автомата А – это множества состояний {1,2,3,4,6,7}, {5}, {8,9}, и перебрасываемые дуги прилежат разным компонентам.
5. Анализ основных видов конечных автоматов
5.1 Детерминированный конечный автомат
Детерминированным конечным автоматом (ДКА) называется машина, распознающая цепочки символов, в которой для каждой последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего (рис. 3). Она имеет входную ленту, разбитую на клетки, головку на входной ленте (входную головку) и управляющее устройство с конечным числом состояний. Конечный автомат М можно представить в виде пятерки (S, L, a, s, F), где
- S – конечное множество состояний устройства управления;
- L – алфавит входных символов;
- a – функция переходов, отображающая S x (I U {i}) в множество подмножеств множества S;
- s – начальное состояние устройства управления;
- F – множество заключительных (допускающих) состояний [5].
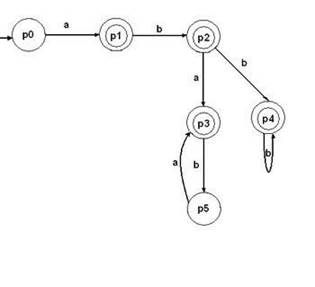
Рисунок 3 – Детерминированный конечный автомат
ДКА выполняет шаги, определяемые текущим состоянием его блока управления и входным символом, обозреваемым входной головкой. Каждый шаг состоит из перехода в новое состояние и сдвига входной головки на одну клетку вправо. Что язык представим регулярным выражением тогда и только тогда, когда он допускается некоторым конечным автоматом [6].
Конечный автомат можно описать с помощью диаграмм состояний и таблиц переходов.
Диаграмма состояний (или иногда граф переходов) – графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого – состояния КА, ребра – переходы из одного состояния в другое, а нагрузка – символы, при которых осуществляется данный переход. Если переход из состояния а1 в а2 может быть осуществлен при появлении одного из нескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они [7].
Таблица переходов – табличное представление функции F. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу – один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.
4.2 Недетерминированный конечный автомат
Недетерминированный конечный автомат – абстрактная машина, которая читает символы из входной цепочки и решает, допустить или отвергнуть эту цепочку. Он может изменить состояние, перейдя из одного состояния в другое. Внутреннюю структуру такого автомата можно представить графом переходов НКА тоже распознаёт цепочки символов, цепочка считается допустимой, если после её обработки множество состояний, в котором оказался автомат, содержит хотя бы одно допускающее. Таким образом, НКА также задаёт некоторый язык [8].
Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали и такие атоматы называются эквивалентными. Однако, поскольку количество состояний в эквивалентном ДКА в худшем случае растёт экспоненциально с ростом количества состояний исходного НКА, на практике подобная детерминизация не всегда возможна. Кроме того, конечные автоматы с выходом в общем случае не поддаются детерминизации.
Для каждого состояния и каждого входного символа НКА имеет ноль или более вариантов выбора следующего шага. Он может также выбирать, сдвигать ему входную головку при изменении состояния или нет [9]. Приведем определение недетерминированного конечного автомата.
Существует дополнительный результат или возможность сопоставить какому-либо взятому НКА эквивалентную «детерминированную» машину. Однако детерминированный конечный автомат, эквивалентный данному НКА с n состояниями, может иметь вплоть до 2 в n степени состояний. Поэтому переход от НКА к детерминированному автомату не всегда дает эффективный способ моделирования недетерминированного конечного автомата [10].
Выводы
Идея применения конечных автоматов является чрезвычайно полезной концепцией, плодотворность которой прошла проверку временем. Использование конечных автоматов позволяет разработчикам создавать хорошо организованные приложения с гибкими возможностями. Их применение позволяет создавать ясный, понятный и надежно функционирующий код.
Использование конечных автоматов стало уже обычной практикой при проектировании приложений для настольных компьютеров, серверов и мобильных устройств.
Преимущества, обеспечиваемые применением конечных автоматов, заметнее всего проявляются в случае приложений для мобильных устройств, требующих экономного расходывания экранного пространства, памяти, вычислительной мощности и других ресурсов.
Список источников
- Смирнова Н.В., Смирнов В.В. Применение теории конечных автоматов в разработке программных систем / Н.В. Смирнова, В.В., Смирнов // Збірник наукових праць Кіровоградського національного технічного університету. Техніка в сільськогосподарському виробництві, галузеве машинобудування, автоматизація. – 2014. – Вип. 27. – С. 316-320.
- Капитонова Ю.В. Основы дискретной математики / Ю.В. Капитонова, С.Л. Кривий, А.А. Летичевский, Г.М. Луцкий, Н.К. Печурин. – К.: Наукова думка, 2002. – 568 с.
- Евтушенко Н.В., Петренко А.Ф. Метод построения проверяющих экспериментов для произвольного недетерминированного автомата / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1990. – № 5. – С. 73-76.
- Кудрявцев В.Б., Грунский И.С., Козловский В.А. Анализ поведения автоматов / В.Б. Кудрявцев, И.С. Грунский, В.А. Козловский // Дискретная математика. – 2009. – №1. – С. 3-35.
- Козловский В.А., Копытова О.М. Представления автоматов относительно m-плотных классов / В.А. Козловский, О.М. Копытова // Матер. VIII Межд. семинара «Дискретная математика и ее приложения» (Москва, 2-6 февраля 2004 г.) – М.: Изд. МГУ. – С. 277-280.
- Швец О.С., Копытова О.М. О сравнении поведения ОДk-эталона и автоматов, порождаемых его локальными преобразованиями / О.С. Швец, О.М. Копытова // Материалы V всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых «Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2014)» (22.04-23.04.2014). Донецк: ДонНТУ, 2014. – С. 365-369.
- Паулин О.Н. Основы теории алгоритмов: учебное пособие / О.Н. Паулин. – Одесса: Автограф, 2005. – 188 с.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл. – М.: Наука, 1966. – 272 с.
- Брауэр Р. Введение в теорию конечных автоматов/ Р. Брауэр. – М.: Радио и связь, 1987. – 392 с.
- Евтушенко Н.В., Лебедев А.В., Петренко А. Ф. О проверяющих экспериментах с недетерминированными автоматами / Н.В. Евтушенко, А.В. Лебедев, А.Ф. Петренко // Автоматика и вычислительная техника. – 1991. – № 6. – С. 81-85.
