Исследование графической системы с параллельным поиском пересечения луча с группой полигональных объектов
Авторы: Мальчева Р.В., Завадская Т.В., Кудояр В.И.
Источник: Исследование графической системы с параллельным поиском пересечения луча с группой
полигональных объектов / Информатика и кибернетика, № 3 (9), Донецк, ДонНТУ, 2017 г., с. 83-88.
Аннотация
Исследование графической системы с вертикальной архитектурой для поиска пересечения луча с группой полигональных объектов. Выполнен анализ архитектурной организации графических систем. Предложена модификация алгоритма поиска пересечения луча с графической сценой. Выполнено проектирование системы с вертикальной архитектурой с использованием UML. Проведены исследования параметров системы поиска пересечения луча с полигональными объектами.
Ключевые слова
Трассировка лучей, архитектура, параллельный поиск, проектирование, UML, исследование.
Введение
Основным недостатком метода трассировки лучей является его трудоемкость. До недавнего времени существовали только системы с программной реализацией данного метода. Однако в последнее 10-летие усилилось внимание и к аппаратной реализации трассировки, в том числе и на FPGA [1, 2]. В полной мере особенностям трассировки лучей соответствуют массивно параллельные вычислительные способности графических процессоров NVIDIA, позволяя существенно увеличить скорость визуализации в многочисленных применениях. NVIDIA поддерживает компании в расширении применения GPU-вычислений на производстве и принимает во внимание их потребности при разработке своих будущих архитектур GPU, языков и инструментов [3, 4].
Постановка задачи
Метод обратной трассировки лучей предполагает выполнение поиска пересечения луча, проведенного из глаза наблюдателя через каждый элемент окна, соответствующий пикселю экрана, с объектами сцены. Поэтому традиционно архитектура системы, основанной на этом методе, реализует принцип распараллеливания «от выходных данных» и по классификации [5] относится, в идеале, к типу «процессор на пиксель», а фактически - к «процессор на фрагмент изображения» [6, 7], хорошо реализуемый на кластерах [8]. Цель выполненных исследований – разработка системы с реализацией параллельного поиска пересечения трассируемого луча с несколькими полигональными объектами, а также установление зависимости времени выполнения данного этапа алгоритма от числа параллельных процессов и сложности объектов. При разработке применено многоуровневое проектирование с использованием UML [9].
Реализация блока поиска пересечения луча с полигональным объектом
На вход блока СR подаются параметры луча, заданные в системе координат объекта: Xv_o, Yv_o, Zv_o - координата начала луча; Vx_o, Vy_o, Vz_o – вектор направления луча. Объект аппроксимирован плоскими выпуклыми гранями, каждая из которых описывается массивом координат вершин {x[n], y[n], z[n]} и нормальным вектором N={nx, ny, nz}. Для анализа используется только 1-я по списку вершина каждой грани. В результате блок формирует признак наличия пересечения (cross), и, если пересечение есть, то номер грани, в которую входит луч (gin) и значение параметра t0 (рис.1).
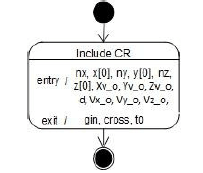
Рисунок 1 – Представление блока CR
Параметр t0 определяет пересечение луча с многогранником и равен отношению числителя (dev) к знаменателю (div), взятому с обратным знаком. Числитель есть подстановка точки начала луча в уравнение плоскости грани (1).
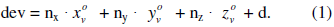
При этом свободный член уравнения плоскости, d, определяется из выражения (2) подстановкой координат любой вершины грани в уравнение.
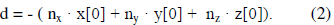
Знаменатель представляет собой скалярное произведение вектора луча на нормальный вектор грани (выражение 3).
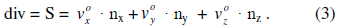
Все три выражения можно рассчитывать параллельно, если выражение (1) заменить на выражения (4, 5).
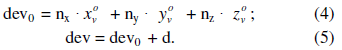
UML-диаграмма блока CR поиска параметра пересечения луча с полигональным объектом приведена на рис.2.

Рисунок 2 – UML-диаграмма блока CR поиска параметра пересечения луча с полигональным объектом
Очевидно, что реализация каждого выражения требует параллельного выполнения трех умножений (устройство М1) и затем двух последовательных сложений (устройство А1) [10]. Соответствующий блок назван Р0ВЬ, его диаграмма на примере вычисления скалярного произведения приведена на рис. 3
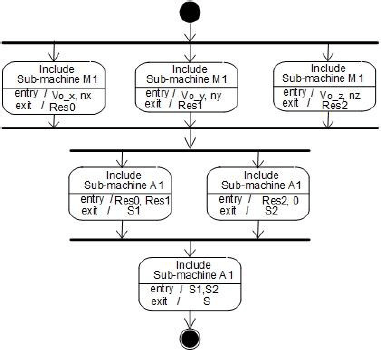
Рисунок 3 - UML-диаграмма блока вычисления скалярного произведения (Р0ВЬ)
Далее блоком СС выполняется умножение координат начала луча, а блоком ССV1 – умножение параметров вектора направления луча на матрицу D[3][3]. Блоки СС и ССV1 включают в себя по 3 параллельных блока, аналогичных Р0ВЬ [10]. Обозначим такой объединенный блок ТО. UML-диаграмма блока CROSS приведена на рис. 5. В ней используются следующие обозначения: hit – число пересечений луча с объектами, gin – номер грани в точке входа луча, Анализ наличия пересечения луча с объектом сводится к анализу tin<tout, т.е. расстояние до точки входа меньше, чем до точки выхода. При этом tin выбирается между параметрами t видимых плоскостей (div<0), а tout - между параметрами невидимых.
Реализация параллельного поиска пересечения луча с группой объектов
Т.к. расчет выражений 1-5 выполняется в системе координат каждого объекта, то кроме блока СА предварительно необходимо выполнить расчет матрицы преобразования из глобальной системы и умножить на эту матрицу параметры луча. Расчет коэффициентов матрицы выполняется блоком MTR2 (рис. 4) по угловым координатам { yr, О, у } вектора Poki положения каждого объекта относительно глобальной системы координат. Входными параметрами параллельных вычислительных устройств являются синусы и косинусы углов, получаемые из расположенных в постоянной памяти таблиц:
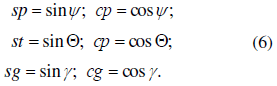
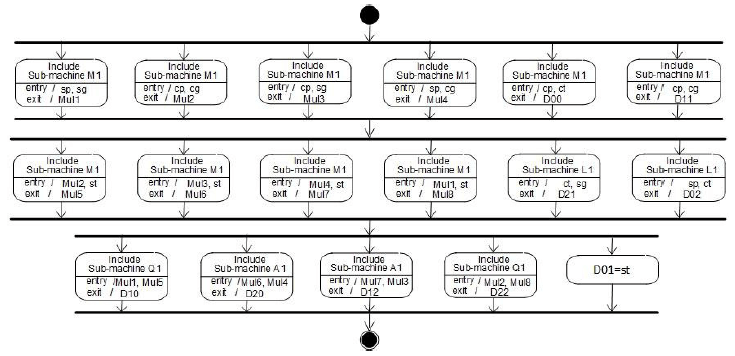
Рисунок 4 - UML-диаграмма блока MTR2 расчета матриц преобразований из глобальной системы координат в систему координат объекта
iob – индекс объекта Kgг – количество групп объектов, вычисляется автоматом деления D1 по выражению (7):
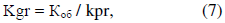
igr – номер группы объектов,обрабатываемых параллельно, kрr - количество параллельно анализируемых объектов, iрr – номер объекта в группе.
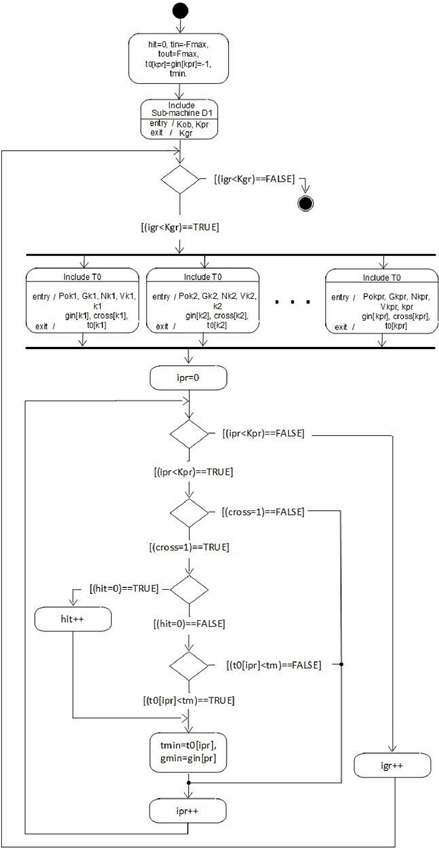
Рисунок 5 - UML-диаграмма блока CROSS поиска пересечения луча с объектами кадра
Если луч пересекает более одного объекта, то в качестве точки входа луча выбирается минимальное значение из t0 объектов группы. В поиске минимума участвует значение, полученное для предыдущих групп объектов.
Исследование системы
Анализ UML-диаграммы блока СЁО показывает, что система поиска пересечения луча с группой полигональных объектов имеет вертикальную архитектуру [5], в ней происходит распараллеливание «от входных данных». Для поведения исследований на базе UML¬диаграмм разработаны модели устройств с использованием языка Verilog [9, 11]. В качестве входных данных использованы базы данных по 5 миллионов полигональных объектов. В исследованиях, результаты которых приведены на рис. 6, варьируется количество объектов в группе (соответственно, число параллельных блоков ТО kpr, заданное по оси абсцисс). По оси ординат приведено полученное временя трассировки сцены, Т, маппинных циклов.
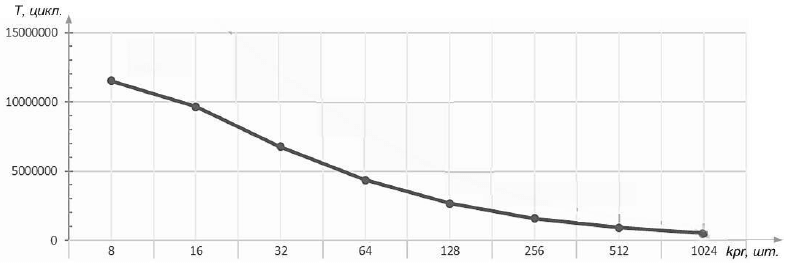
Рисунок 6 - Зависимость времени трассировки сцены от количества параллельных блоков Т0
В исследованиях, результаты которых приведены на рис. 7, время трассировки, Т, задано в миллионах маппинных циклов. При этом кроме количества объектов в группе варьируется сложность полигональных объектов. Число граней принято равным 4, 8, 12, 24 и 36 – им соответствую кривые, обозначенные С4 – С36..
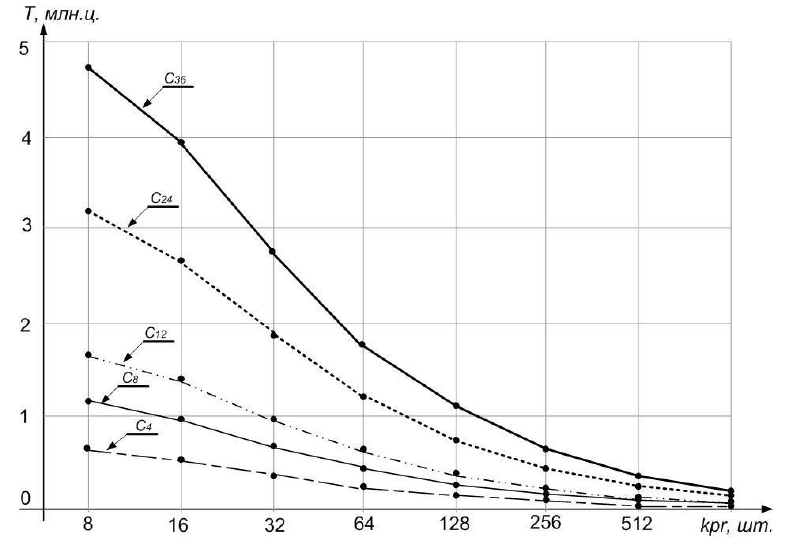
Рисунок 7 - Зависимость времени трассировки сцены от количества параллельных блоков ТО и сложности объектов
Заключение
Анализ зависимостей, приведенных на рис. 6 и рис. 7, показывает, что увеличение количества параллельных блоков Т0 в 2 раза уменьшает время трассировки менее, чем в 2 раза. Причем, с увеличением количества объектов в группе выигрыш в производительности становится все менее заметен. Это связано с дополнительными затратами на распределение объектов по процессам вертикального конвейера. Более 512 вычислительных процессов применять не имеет смысла, что вполне соответствует размерам матриц технологии CUDA.
Список использованной литературы
1. Schmittler J. Realtime Ray Tracing of Dynamic Scenes on an FPGA Chip // Computer Science, Saarland University, 2004. - PP. 8.
2. Malcheva R. An Acceleration of FPGA-based Ray Tracer / R. Malcheva, M. Yunis // European Scientific Journal, 2014. - Vol.10, N7. – PP. 186-190.
3. Компании, использующие GPU для трассировки лучей [Электронный ресурс]– Режим доступа: http://www.nvidia.ru/object/gpu-ray-tracing-ru.html
4. NVIDIA обеспечивает широкую доступность физически корректного рендеринга [Электронный ресурс] – Режим доступа: http://www.nvidia.ru/object/blog-nvidia-pbr-gtc-ru.html
5. Computer Graphics: Principles and Practice, Third Edition / John F. Hughes, Andries van Dam, Morgan McGuire, David Sklar, James D. Foley. - Addison-Wesley, 2014. – 1209 р.
6. Bashkov E.A. Synthesis of an image of enclosing circumstances in view of a physical condition of an atmosphere / E.A. Bashkov. – Electronic simulation, 1996. –Vol.18. - N3. - PP. 45- 51.
7. Bashkov E.A. Accelerating Search for Ray-Object Intersection Point in the Ray Tracing Method. - Engineering Simulation, 1996. - Vol.13. - N3. - РР. 369 - 380.
8. Мальчева Р.В. Реализация модифициро-ванного алгоритма трассировки лучей на кластере NeClus / Р.В. Мальчева, М. Юнис // Науковг працг Донецького нацгонального технгчного унгверситету. Сергя: «Обчислювальна технгка та автоматизацгя». – Донецьк: ДонНТУ, 2013. – Ns1(24)’2013. - С. 263-268.
9. Malcheva R. Application of multilevel design on the base of UML for digital system developing // in book “Design of Digital Systems and Devices. Series: Lecture Notes in Electrical Engineering. – Springer-Verlag Berlin Heildelberg, 2011. – Vol. 79. - РР. 93-117.
10. Попова А.Н. Разработка устройства поиска пересечения луча с полигональным объектом / А.Н. Попова, А.В. Селинова, Р.В. Мальчева // «Компьютерная и программная инженерия. Сборник материалов междунуродной научно-практической конференции студентов, аспирантов и молодых ученых» (г. Донецк, ДонНТУ, 2015 г.) – С. 242-247.
11. Хаханов В.И. Проектирование и верификация цифровых систем на кристаллах. Verilog & System Verilog / В.И. Хаханов, И.В. Хаханова, Е.И. Литвинова, О.А. Гузь. – Харьков: ХНУРЭ, 2010. – 528 с.