Article · November 2015
CITATIONS
READS
14
20,241
2 authors, including:
11 PUBLICATIONS
25 CITATIONS
Some of the authors of this publication are also working on these related projects:
Identification and Validation of Low-Cost, High-Throughput Microbial and Metabolite Biomarker Assays for Lung Cancer Status, Stage and Type View project
The user has requested enhancement of the downloaded file.
An Introduction to Convolutional Neural Networks
Keiron O’Shea1 and Ryan Nash2
1
Department of Computer Science, Aberystwyth University, Ceredigion, SY23 3DB
keo7@aber.ac.uk
2
School of Computing and Communications, Lancaster University, Lancashire, LA1
4YW
nashrd@live.lancs.ac.uk
Abstract. The field of machine learning has taken a dramatic twist in re-
cent times, with the rise of the Artificial Neural Network (ANN). These
biologically inspired computational models are able to far exceed the per-
formance of previous forms of artificial intelligence in common machine
learning tasks. One of the most impressive forms of ANN architecture is
that of the Convolutional Neural Network (CNN). CNNs are primarily
used to solve difficult image-driven pattern recognition tasks and with
their precise yet simple architecture, offers a simplified method of getting
started with ANNs.
This document provides a brief introduction to CNNs, discussing recently
published papers and newly formed techniques in developing these bril-
liantly fantastic image recognition models. This introduction assumes you
are familiar with the fundamentals of ANNs and machine learning.
Keywords: Pattern recognition, artificial neural networks, machine learn-
ing, image analysis
1
Introduction
Artificial Neural Networks (ANNs) are computational processing systems of
which are heavily inspired by way biological nervous systems (such as the hu-
man brain) operate. ANNs are mainly comprised of a high number of intercon-
nected computational nodes (referred to as neurons), of which work entwine in
a distributed fashion to collectively learn from the input in order to optimise its
final output.
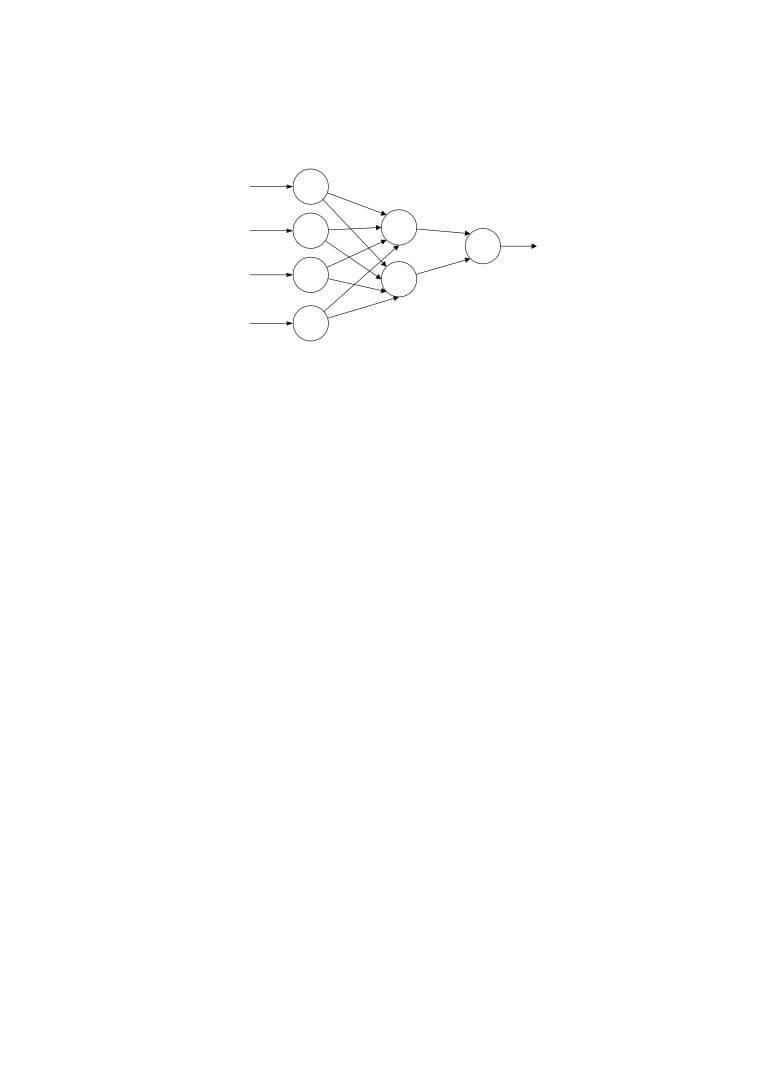
The basic structure of a ANN can be modelled as shown in Figure 1. We would
load the input, usually in the form of a multidimensional vector to the input
layer of which will distribute it to the hidden layers. The hidden layers will then
make decisions from the previous layer and weigh up how a stochastic change
within itself detriments or improves the final output, and this is referred to as
the process of learning. Having multiple hidden layers stacked upon each-other
is commonly called deep learning.
2
Keiron O’Shea et al.
Input Layer
Hidden Layer
Output Layer
Input 1
Input 2
Output
Input 3
Input 4
Fig. 1: A simple three layered feedforward neural network (FNN), comprised
of a input layer, a hidden layer and an output layer. This structure is the basis
of a number of common ANN architectures, included but not limited to Feed-
forward Neural Networks (FNN), Restricted Boltzmann Machines (RBMs) and
Recurrent Neural Networks (RNNs).
The two key learning paradigms in image processing tasks are supervised and
unsupervised learning. Supervised learning is learning through pre-labelled
inputs, which act as targets. For each training example there will be a set of
input values (vectors) and one or more associated designated output values.
The goal of this form of training is to reduce the models overall classification
error, through correct calculation of the output value of training example by
training.
Unsupervised learning differs in that the training set does not include any la-
bels. Success is usually determined by whether the network is able to reduce or
increase an associated cost function. However, it is important to note that most
image-focused pattern-recognition tasks usually depend on classification using
supervised learning.
Convolutional Neural Networks (CNNs) are analogous to traditional ANNs
in that they are comprised of neurons that self-optimise through learning. Each
neuron will still receive an input and perform a operation (such as a scalar
product followed by a non-linear function) - the basis of countless ANNs. From
the input raw image vectors to the final output of the class score, the entire of
the network will still express a single perceptive score function (the weight).
The last layer will contain loss functions associated with the classes, and all of
the regular tips and tricks developed for traditional ANNs still apply.
The only notable difference between CNNs and traditional ANNs is that CNNs
are primarily used in the field of pattern recognition within images. This allows
us to encode image-specific features into the architecture, making the network
Introduction to Convolutional Neural Networks
3
more suited for image-focused tasks - whilst further reducing the parameters
required to set up the model.
One of the largest limitations of traditional forms of ANN is that they tend to
struggle with the computational complexity required to compute image data.
Common machine learning benchmarking datasets such as the MNIST database
of handwritten digits are suitable for most forms of ANN, due to its relatively
small image dimensionality of just 28 × 28. With this dataset a single neuron in
the first hidden layer will contain 784 weights (28 × 28 × 1 where 1 bare in mind
that MNIST is normalised to just black and white values), which is manageable
for most forms of ANN.
If you consider a more substantial coloured image input of 64 × 64, the number
of weights on just a single neuron of the first layer increases substantially to
12, 288. Also take into account that to deal with this scale of input, the network
will also need to be a lot larger than one used to classify colour-normalised
MNIST digits, then you will understand the drawbacks of using such models.
1.1
Overfitting
But why does it matter? Surely we could just increase the number of hidden lay-
ers in our network, and perhaps increase the number of neurons within them?
The simple answer to this question is no. This is down to two reasons, one be-
ing the simple problem of not having unlimited computational power and time
to train these huge ANNs.
The second reason is stopping or reducing the effects of overfitting. Overfitting
is basically when a network is unable to learn effectively due to a number of
reasons. It is an important concept of most, if not all machine learning algo-
rithms and it is important that every precaution is taken as to reduce its effects.
If our models were to exhibit signs of overfitting then we may see a reduced
ability to pinpoint generalised features for not only our training dataset, but
also our test and prediction sets.
This is the main reason behind reducing the complexity of our ANNs. The less
parameters required to train, the less likely the network will overfit - and of
course, improve the predictive performance of the model.
2
CNN architecture
As noted earlier, CNNs primarily focus on the basis that the input will be com-
prised of images. This focuses the architecture to be set up in way to best suit
the need for dealing with the specific type of data.
4
Keiron O’Shea et al.
One of the key differences is that the neurons that the layers within the CNN
are comprised of neurons organised into three dimensions, the spatial dimen-
sionality of the input (height and the width) and the depth. The depth does not
refer to the total number of layers within the ANN, but the third dimension of a
activation volume. Unlike standard ANNS, the neurons within any given layer
will only connect to a small region of the layer preceding it.
In practice this would mean that for the example given earlier, the input ’vol-
ume’ will have a dimensionality of 64 × 64 × 3 (height, width and depth), lead-
ing to a final output layer comprised of a dimensionality of 1 × 1 × n (where
n represents the possible number of classes) as we would have condensed the
full input dimensionality into a smaller volume of class scores filed across the
depth dimension.
2.1
Overall architecture
CNNs are comprised of three types of layers. These are convolutional layers,
pooling layers and fully-connected layers. When these layers are stacked, a
CNN architecture has been formed. A simplified CNN architecture for MNIST
classification is illustrated in Figure 2.
convolution
w/ReLu pooling
fully-connected
0
9
input
output
fully-connected
w/ ReLu
Fig. 2: An simple CNN architecture, comprised of just five layers
The basic functionality of the example CNN above can be broken down into
four key areas.
1. As found in other forms of ANN, the input layer will hold the pixel values
of the image.
2. The convolutional layer will determine the output of neurons of which are
connected to local regions of the input through the calculation of the scalar
product between their weights and the region connected to the input vol-
ume. The rectified linear unit (commonly shortened to ReLu) aims to apply
Introduction to Convolutional Neural Networks
5
an ’elementwise’ activation function such as sigmoid to the output of the
activation produced by the previous layer.
3. The pooling layer will then simply perform downsampling along the spa-
tial dimensionality of the given input, further reducing the number of pa-
rameters within that activation.
4. The fully-connected layers will then perform the same duties found in
standard ANNs and attempt to produce class scores from the activations,
to be used for classification. It is also suggested that ReLu may be used
between these layers, as to improve performance.
Through this simple method of transformation, CNNs are able to transform
the original input layer by layer using convolutional and downsampling tech-
niques to produce class scores for classification and regression purposes.
Fig. 3: Activations taken from the first convolutional layer of a simplistic deep
CNN, after training on the MNIST database of handwritten digits. If you look
carefully, you can see that the network has successfully picked up on character-
istics unique to specific numeric digits.
However, it is important to note that simply understanding the overall archi-
tecture of a CNN architecture will not suffice. The creation and optimisation
of these models can take quite some time, and can be quite confusing. We will
now explore in detail the individual layers, detailing their hyperparameters
and connectivities.
2.2
Convolutional layer
As the name implies, the convolutional layer plays a vital role in how CNNs
operate. The layers parameters focus around the use of learnable kernels.
6
Keiron O’Shea et al.
These kernels are usually small in spatial dimensionality, but spreads along the
entirety of the depth of the input. When the data hits a convolutional layer,
the layer convolves each filter across the spatial dimensionality of the input to
produce a 2D activation map. These activation maps can be visualised, as seen
in Figure 3.
As we glide through the input, the scalar product is calculated for each value in
that kernel. (Figure 4) From this the network will learn kernels that ’fire’ when
they see a specific feature at a given spatial position of the input. These are
commonly known as activations.
Input Vector
0
0
0
0
0
0
Pooled Vector
Kernel
Destination Pixel
0
1
2
1
1
2
0
0
0
4
0
0
0
1
1
1
1
1
0
1
2
0
0
0
-8
1
0
0
0
0
0
0
1
1
0
0
-4
0
0
1
1
1
0
0
1
1
1
1
1
Fig. 4: A visual representation of a convolutional layer. The centre element of the
kernel is placed over the input vector, of which is then calculated and replaced
with a weighted sum of itself and any nearby pixels.
Every kernel will have a corresponding activation map, of which will be stacked
along the depth dimension to form the full output volume from the convolu-
tional layer.
As we alluded to earlier, training ANNs on inputs such as images results in
models of which are too big to train effectively. This comes down to the fully-
connected manner of standard ANN neurons, so to mitigate against this every
neuron in a convolutional layer is only connected to small region of the input
volume. The dimensionality of this region is commonly referred to as the re-
ceptive field size of the neuron. The magnitude of the connectivity through the
depth is nearly always equal to the depth of the input.
For example, if the input to the network is an image of size 64 × 64 × 3 (a RGB-
coloured image with a dimensionality of 64 × 64) and we set the receptive field
size as 6 × 6, we would have a total of 108 weights on each neuron within the
convolutional layer. (6 × 6 × 3 where 3 is the magnitude of connectivity across
the depth of the volume) To put this into perspective, a standard neuron seen
in other forms of ANN would contain 12, 288 weights each.
Convolutional layers are also able to significantly reduce the complexity of the
model through the optimisation of its output. These are optimised through
three hyperparameters, the depth, the stride and setting zero-padding.
Introduction to Convolutional Neural Networks
7
The depth of the output volume produced by the convolutional layers can be
manually set through the number of neurons within the layer to a the same
region of the input. This can be seen with other forms of ANNs, where the
all of the neurons in the hidden layer are directly connected to every single
neuron beforehand. Reducing this hyperparameter can significantly minimise
the total number of neurons of the network, but it can also significantly reduce
the pattern recognition capabilities of the model.
We are also able to define the stride in which we set the depth around the spatial
dimensionality of the input in order to place the receptive field. For example if
we were to set a stride as 1, then we would have a heavily overlapped receptive
field producing extremely large activations. Alternatively, setting the stride to a
greater number will reduce the amount of overlapping and produce an output
of lower spatial dimensions.
Zero-padding is the simple process of padding the border of the input, and
is an effective method to give further control as to the dimensionality of the
output volumes.
It is important to understand that through using these techniques, we will alter
the spatial dimensionality of the convolutional layers output. To calculate this,
you can make use of the following formula:
(V − R) + 2Z
S+1
Where V represents the input volume size (height×width×depth), R represents
the receptive field size, Z is the amount of zero padding set and S referring to
the stride. If the calculated result from this equation is not equal to a whole
integer then the stride has been incorrectly set, as the neurons will be unable to
fit neatly across the given input.
Despite our best efforts so far we will still find that our models are still enor-
mous if we use an image input of any real dimensionality. However, methods
have been developed as to greatly curtail the overall number of parameters
within the convolutional layer.
Parameter sharing works on the assumption that if one region feature is useful
to compute at a set spatial region, then it is likely to be useful in another region.
If we constrain each individual activation map within the output volume to the
same weights and bias, then we will see a massive reduction in the number of
parameters being produced by the convolutional layer.
As a result of this as the backpropagation stage occurs, each neuron in the out-
put will represent the overall gradient of which can be totalled across the depth
- thus only updating a single set of weights, as opposed to every single one.
8
Keiron O’Shea et al.
2.3
Pooling layer
Pooling layers aim to gradually reduce the dimensionality of the representa-
tion, and thus further reduce the number of parameters and the computational
complexity of the model.
The pooling layer operates over each activation map in the input, and scales
its dimensionality using the “MAX” function. In most CNNs, these come in the
form of max-pooling layers with kernels of a dimensionality of 2 × 2 applied
with a stride of 2 along the spatial dimensions of the input. This scales the
activation map down to 25% of the original size - whilst maintaining the depth
volume to its standard size.
Due to the destructive nature of the pooling layer, there are only two generally
observed methods of max-pooling. Usually, the stride and filters of the pooling
layers are both set to 2 × 2, which will allow the layer to extend through the
entirety of the spatial dimensionality of the input. Furthermore overlapping
pooling may be utilised, where the stride is set to 2 with a kernel size set to
3. Due to the destructive nature of pooling, having a kernel size above 3 will
usually greatly decrease the performance of the model.
It is also important to understand that beyond max-pooling, CNN architectures
may contain general-pooling. General pooling layers are comprised of pooling
neurons that are able to perform a multitude of common operations including
L1/L2-normalisation, and average pooling. However, this tutorial will primar-
ily focus on the use of max-pooling.
2.4
Fully-connected layer
The fully-connected layer contains neurons of which are directly connected to
the neurons in the two adjacent layers, without being connected to any layers
within them. This is analogous to way that neurons are arranged in traditional
forms of ANN. (Figure 1)
3
Recipes
Despite the relatively small number of layers required to form a CNN, there
is no set way of formulating a CNN architecture. That being said, it would be
idiotic to simply throw a few of layers together and expect it to work. Through
reading of related literature it is obvious that much like other forms of ANNs,
CNNs tend to follow a common architecture. This common architecture is illus-
trated in Figure 2, where convolutional layers are stacked, followed by pooling
layers in a repeated manner before feeding forward to fully-connected layers.
Introduction to Convolutional Neural Networks
9
Another common CNN architecture is to stack two convolutional layers before
each pooling layer, as illustrated in Figure 5. This is strongly recommended as
stacking multiple convolutional layers allows for more complex features of the
input vector to be selected.
convolution w/ ReLu
pooling
convolution w/ ReLu
pooling
pooling
fully-connected
0
9
input
output
convolution
fully-connected
w/ ReLu
w/ ReLu
Fig. 5: A common form of CNN architecture in which convolutional layers are
stacked between ReLus continuously before being passed through the pooling
layer, before going between one or many fully connected ReLus.
It is also advised to split large convolutional layers up into many smaller sized
convolutional layers. This is to reduce the amount of computational complexity
within a given convolutional layer. For example, if you were to stack three con-
volutional layers on top of each other with a receptive field of 3×3. Each neuron
of the first convolutional layer will have a 3 × 3 view of the input vector. A neu-
ron on the second convolutional layer will then have a 5 × 5 view of the input
vector. A neuron on the third convolutional layer will then have a 7 × 7 view of
the input vector. As these stacks feature non-linearities which in turn allows us
to express stronger features of the input with fewer parameters. However, it is
important to understand that this does come with a distinct memory allocation
problem - especially when making use of the backpropagation algorithm.
The input layer should be recursively divisible by two. Common numbers in-
clude 32 × 32, 64 × 64, 96 × 96, 128 × 128 and 224 × 224.
Whilst using small filters, set stride to one and make use of zero-padding as to
ensure that the convolutional layers do not reconfigure any of the dimension-
ality of the input. The amount of zero-padding to be used should be calculated
by taking one away from the receptive field size and dividing by two.activation
CNNs are extremely powerful machine learning algorithms, however they can
be horrendously resource-heavy. An example of this problem could be in filter-
ing a large image (anything over 128 × 128 could be considered large), so if the
input is 227 × 227 (as seen with ImageNet) and we’re filtering with 64 kernels
each with a zero padding of then the result will be three activation vectors of
size 227 × 227 × 64 - which calculates to roughly 10 million activations - or an
enormous 70 megabytes of memory per image. In this case you have two op-
tions. Firstly, you can reduce the spatial dimensionality of the input images by
10
Keiron O’Shea et al.
resizing the raw images to something a little less heavy. Alternatively, you can
go against everything we stated earlier in this document and opt for larger filter
sizes with a larger stride (2, as opposed to 1).
In addition to the few rules-of-thumb outlined above, it is also important to ac-
knowledge a few ’tricks’ about generalised ANN training techniques. The au-
thors suggest a read of Geoffrey Hinton’s excellent “Practical Guide to Training
Restricted Boltzmann Machines”.
4
Conclusion
Convolutional Neural Networks differ to other forms of Artifical Neural Net-
work in that instead of focusing on the entirety of the problem domain, knowl-
edge about the specific type of input is exploited. This in turn allows for a much
simpler network architecture to be set up.
This paper has outlined the basic concepts of Convolutional Neural Networks,
explaining the layers required to build one and detailing how best to structure
the network in most image analysis tasks.
Research in the field of image analysis using neural networks has somewhat
slowed in recent times. This is partly due to the incorrect belief surrounding the
level of complexity and knowledge required to begin modelling these superbly
powerful machine learning algorithms. The authors hope that this paper has
in some way reduced this confusion, and made the field more accessible to
beginners.
Acknowledgements
The authors would like to thank Dr. Chuan Lu and Nicholas Dimonaco for
useful discussion and suggestions.
References
1. Ciresan, D., Meier, U., Schmidhuber, J.: Multi-column deep neural networks for im-
age classification. In: Computer Vision and Pattern Recognition (CVPR), 2012 IEEE
Conference on. pp. 3642-3649. IEEE (2012)
2. Cire¸an, D.C., Giusti, A., Gambardella, L.M., Schmidhuber, J.: Mitosis detection in
breast cancer histology images with deep neural networks. In: Medical Image Com-
puting and Computer-Assisted Intervention-MICCAI 2013, pp. 411-418. Springer
(2013)
3. Ciresan, D.C., Meier, U., Masci, J., Maria Gambardella, L., Schmidhuber, J.: Flexible,
high performance convolutional neural networks for image classification. In: IJCAI
Proceedings-International Joint Conference on Artificial Intelligence. vol. 22, p. 1237
(2011)
Introduction to Convolutional Neural Networks
11
4.
Cire¸an, D.C., Meier, U., Gambardella, L.M., Schmidhuber, J.: Convolutional neural
network committees for handwritten character classification. In: Document Analysis
and Recognition (ICDAR), 2011 International Conference on. pp. 1135-1139. IEEE
(2011)
5.
Egmont-Petersen, M., de Ridder, D., Handels, H.: Image processing with neural net-
worksa review. Pattern recognition 35(10), 2279-2301 (2002)
6.
Farabet, C., Martini, B., Akselrod, P., Talay, S., LeCun, Y., Culurciello, E.: Hardware
accelerated convolutional neural networks for synthetic vision systems. In: Circuits
and Systems (ISCAS), Proceedings of 2010 IEEE International Symposium on. pp.
257-260. IEEE (2010)
7.
Hinton, G.: A practical guide to training restricted boltzmann machines. Momentum
9(1), 926 (2010)
8.
Hinton, G.E., Srivastava, N., Krizhevsky, A., Sutskever, I., Salakhutdinov, R.R.: Im-
proving neural networks by preventing co-adaptation of feature detectors. arXiv
preprint arXiv:1207.0580 (2012)
9.
Ji, S., Xu, W., Yang, M., Yu, K.: 3d convolutional neural networks for human action
recognition. Pattern Analysis and Machine Intelligence, IEEE Transactions on 35(1),
221-231 (2013)
10.
Karpathy, A., Toderici, G., Shetty, S., Leung, T., Sukthankar, R., Fei-Fei, L.: Large-
scale video classification with convolutional neural networks. In: Computer Vision
and Pattern Recognition (CVPR), 2014 IEEE Conference on. pp. 1725-1732. IEEE
(2014)
11.
Krizhevsky, A., Sutskever, I., Hinton, G.E.: Imagenet classification with deep convo-
lutional neural networks. In: Advances in neural information processing systems.
pp. 1097-1105 (2012)
12.
LeCun, Y., Boser, B., Denker, J.S., Henderson, D., Howard, R.E., Hubbard, W., Jackel,
L.D.: Backpropagation applied to handwritten zip code recognition. Neural compu-
tation 1(4), 541-551 (1989)
13.
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to doc-
ument recognition. Proceedings of the IEEE 86(11), 2278-2324 (1998)
14.
Nebauer, C.: Evaluation of convolutional neural networks for visual recognition.
Neural Networks, IEEE Transactions on 9(4), 685-696 (1998)
15.
Simard, P.Y., Steinkraus, D., Platt, J.C.: Best practices for convolutional neural net-
works applied to visual document analysis. In: null. p. 958. IEEE (2003)
16.
Srivastava, N.: Improving neural networks with dropout. Ph.D. thesis, University of
Toronto (2013)
17.
Szarvas, M., Yoshizawa, A., Yamamoto, M., Ogata, J.: Pedestrian detection with con-
volutional neural networks. In: Intelligent Vehicles Symposium, 2005. Proceedings.
IEEE. pp. 224-229. IEEE (2005)
18.
Szegedy, C., Toshev, A., Erhan, D.: Deep neural networks for object detection. In:
Advances in Neural Information Processing Systems. pp. 2553-2561 (2013)
19.
Tivive, F.H.C., Bouzerdoum, A.: A new class of convolutional neural networks
(siconnets) and their application of face detection. In: Neural Networks, 2003. Pro-
ceedings of the International Joint Conference on. vol. 3, pp. 2157-2162. IEEE (2003)
20.
Zeiler, M.D., Fergus, R.: Stochastic pooling for regularization of deep convolutional
neural networks. arXiv preprint arXiv:1301.3557 (2013)
21.
Zeiler, M.D., Fergus, R.: Visualizing and understanding convolutional networks. In:
Computer Vision-ECCV 2014, pp. 818-833. Springer (2014)
View publication stats