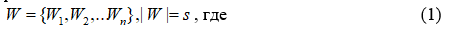
УДК 004.67
ПРИМЕНЕНИЕ АЛГОРИТМОВ НЕЧЕТКОГО ПОИСКА ДЛЯ ОПТИМИЗАЦИИ ПОИСКА ИНФОРМАЦИИ В ИНТЕРНЕТ-МАГАЗИНЕ
Моргун И.С., Савкова Е.О.
Донецкий национальный технический университет
кафедра автоматизированных систем управления
E-mail: igooorr21@gmail.com
Аннотация:
Моргун И.С. Применение алгоритмов нечеткого поиска для оптимизации поиска информации в интернет-магазине. Рассмотрен основной принцип отбора данных. Проведен анализ существующих методов и алгоритмов, решающие поставленные задачи. Определен подход оптимизации данных.
Annotation:
Morgun I.S. Application of fuzzy search algorithms to optimization of information in online-shop. The basic principle of data selection. The analysis of existing methods and algorithms that will help to solve tasks. The approach to data optimization is defined.
Введение
В современном мире актуально заказывать различную продукцию через интернет-магазин. Пользователю не нужно тратить особо много времени и сил, что б добраться до магазина, а всего лишь достаточно иметь дома выход в сеть Интернет. Пользователь заходит в Интернет, находит любой интернет-магазин, в котором подбирает себе нужный товар и оформляет заказ. Популяризация такого вида продаж товаров привела к росту количества интернет-магазинов.
Наверное, не многие задумывались, как реализован поиск в интернет-магазине?
В большинстве случаев пользователь, впервые посетив Ваш сайт в поисках чего-либо важного, не станет разбираться в панелях навигации, меню и прочих элементах, а в спешке попытается найти что-нибудь похожее на поисковую строку. Введет туда свой запрос и будет ожидать ответа. Но может случиться так, что Ваша система слишком долго будет обрабатывать запрос пользователя или вовсе не сможет выдать ему ответ. В результате чего, пользователь Вашего сайта просто закроет вкладку и пойдет искать другой сайт.
Общая постановка проблемы
Поиск информации в интернет-магазине - это важная составляющая, и многие посетители будут пользоваться данной функцией. Поэтому, необходимо уделить должное внимание поиску в интернет-магазине. Рассмотрим принцип работы одного из интернет-магазина.
Посетитель заходит на сайт интернет-магазина. Ищет поисковую строку и вводит свой запрос, подтверждает его и ожидает ответа. Система, после отправки запроса пользователем, ожидает его приема и начинает его обрабатывать.
Внутри системы поиск работает так:
Отобранные товары с минимальной информацией (цена, название, характеристики и т.д.), будут переданы назад пользователю в виде ответа на его запрос.
Но существуют ряд недостатков, которые мешают нормальному выполнению поиска и отбора информации в системе. Это могут быть проблемы, связанные с:
Одним из методов устранения этих недостатков и оптимизации поиска информации по запросам пользователей является использование алгоритмов нечеткого поиска (известных как поиск по сходству или fuzzy string search).
Цель данной работы заключается в обзоре и анализе существующих методов и алгоритмов поиска в интернет-магазине.
Постановка задачи
Исходя из трех основных задач нечеткого поиска:
Первая задача является достаточно «тривиальной», имеет достаточное число реализованных методов оптимально выполняющие эту задачу и не требует детального анализа. Для данной исследовательской работы будет рассмотрена вторая задача.
Задачи нечеткого поиска сводятся к тому, что необходимо для каждого слова из заданного n-размерного текста (массива слов), найти совпадения в m-размерном словаре. При этом поиск необходимо выполнить с учетом всевозможных различий (совпадение корня слова и т.п.).
С учетом этого принципа работы поиска, выделим следующие задачи:
Математическая постановка
Для данной задачи мы имеем исходные данные, представленные в виде запроса пользователя W, который он ввел в поисковой строке. Длина этого запроса может быть Wn-слов. Данный запрос имеет такие ограничения:
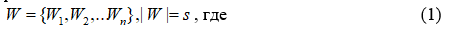
s – любая длина поискового запроса,
Также, имеется словарь U размерности m. Словарь содержит подмножество
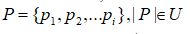 - содержащий некую информацию о товарах, которые он и индексирует у себя. Словарь имеет такие ограничения:
- содержащий некую информацию о товарах, которые он и индексирует у себя. Словарь имеет такие ограничения:

Имея заданный поисковый запрос W пользователя, нам необходимо выбрать из словаря U подмножество P всех слов. А мера отличия d при сравнении поискового запроса между словарем должна не превышать некоторого порогового числа N. Если подмножество P удовлетворяет этому условию, то из словаря будет добавлено это подмножество (товар и его информация) в массив ответа пользователю с информацией о товаре.
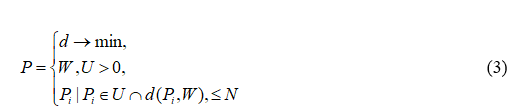
Мера отличия стремиться к минимальному числу расхождения при сравнении поискового запроса с подмножеством из словаря. Для нахождения меры отличия используем один из нижеописанных методов.
Обзор алгоритмов и методов поиска
Задача методов нечеткого поиска заключается в отборе совпадений заданного слова (или начинающиеся с этого слова) из N-размерного текста или словаря. Одной из характерных черт алгоритма нечеткого поиска является метрика.
Метрика – это функция расстояния между двумя словами, позволяющая оценить степень их сходства в данном контексте. Строгое математическое определение метрики (X — множество слов, p — метрика) [1]:

Расстояние Хемминга
Расстояние Хэмминга – мера различающихся позиций для объектов с одинаковой длинной. Широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д [2].
Основным недостатком расстояния редактирования Хэмминга является требование одинаковой длины строк, таким образом, расстояние Хэмминга подходит для расчета расстояния редактирования с учетом таких искажений, как замена и транспозиция, но не подходит при вставках и удалениях.
Джаро-Винклер
Сходство Джаро-Винклера (Jaro-Winkler similarity) было применено в переписи США и использовано в последующей обработке [2].
Для данных строк string1 и string2, их сходство задаётся формулой:

m - число соответствующих символов
a - длина string1
b - длина string2
t - число перестановок
Два символа считаются соответствующими, только если они находятся не дальше чем (max(a,b)/2 - 1). Первый соответствующий символ в string1 сравнивается с первым соответствующим символом в string2; второй соответствующий символ в string1 сравнивается со вторым соответствующим символом в string2, и так далее. Число соответствующих символов делённое на 2 даёт число перестановок.
Улучшенный метод Джаро-Винклера использует веса отличные от 1/3. Он также даёт меньший вес некоторым типам ошибок: визуального сканирования, клавишного ввода и в конце строки.
Распознавание форм Ратклиффа/Обершелпа (алгоритм Оливера)

Km - число совпадающих символов,
|S1|, |S2| - длина сравнивающихся слов
Дистанция редактирования (Расстояние Левенштейна и Дамерау – Левенштейна)
Расстояние Левенштейна ищет минимальное количество действий (вставок, удаления и замены одного символа на другой), необходимых для превращения одной строки в другую. Метод широко используется для исправления ошибок в словах (грамматика поисковых систем), сравнения текстовых файлов или даже генов и хромосом. [3]
Преобразовать одно слово в другое можно различными способами, количество действий также может быть разным. При вычислении расстояния Левенштейна следует выбирать минимальное количество действий.
Если поиск слова осуществляется в тексте, который набран с клавиатуры, то вместо расстояния Левенштейна используют усовершенствованное расстояние Дамерау – Левенштейна.
Алгоритм Вагнера – Фишера позволяет получать расстояние Дамерау – Левенштейна.
Методы поиска с использованием индексов
Особо интересными являются алгоритмы поиска с индексацией.
Представим, одновременно более 30 человек выполняют поисковые запросы. Сервер принимает каждое соединение, управление потоком передается интерпретатору. При каждом запросе заново инициализируется поисковый движок, заново прерывается содержимое сайта. Сложно сказать, сколько времени и ресурсов потребуется, чтобы обработать все эти запросы. Для исключения проделывания одной и той же работы, была придумана технология индексирования.
Индексирование выполняется только при изменении или добавлении содержимого сайта, а поиск выполняется уже по индексу, а не по содержимому.
Особенностью всех алгоритмов нечеткого поиска с индексацией является то, что индекс строится по словарю, составленному по исходному тексту или списку записей в какой-либо базе данных.
Наиболее распространенные из алгоритмов:
Алгоритм расширения выборки
Он основан на сведении задачи о нечетком поиске к задаче о точном поиске.
Суть данного метода заключается в построении множества всевозможных «ошибочных» слов, например, получающихся в результате одной операции редактирования Левенштейна, после чего построенные поисковые запросы ищутся в словаре на точное совпадение.
Одним из недостатков данного алгоритма то, что время его работы сильно зависит от числа k ошибок и от размера алфавита A, и в случае использования поиска по словарю составляет [5]:

Σ – размер алфавита,
n – размер слова,
k – число ошибок.
Например, если для поиска с k = 1 требуется выполнить 300-500 «точных» запросов к словарю, то для k = 2 требуется не менее 10000 запросов.
Следует отметить, что в некоторых случаях можно ограничить класс операций замен и достичь приемлемого сочетания полноты и качества поиска.
Особенность данного алгоритма заключается в том, что он: не требует никакой предварительной обработки словаря; экономит память за счет использования не всего словаря.
Метод Триграмма (N-грамма)
Триграммное сходство (trigram similarity) между двумя строками определяется числом совпадающих символьных триплетов в обоих строках. Алгоритм можно обобщить на n-граммы, где n=1, 2, ... Строки string1 и string2 пополняются слева и справа одним символом пробела. Затем строки разделяются на триплеты (триграммы). Окончательно, сходство вычисляется по формуле [2]:

m - число совпадающих триграмм,
a и b - число триграмм в string1 и string2
Особенность данного метода заключается в простоте реализации. Но чем меньше длина слова и чем больше в нем ошибок, тем выше шанс того, что оно не попадет в соответствующие N-граммам запроса списки, и не будет присутствовать в результате. За счет чего необходимо модифицировать данный метод или же использовать более эффективных методов.
Эти все методы и алгоритмы используют различные подходы к решению проблемы — одни из них используют сведение к точному поиску, другие используют свойства метрики для построения различных пространственных структур. Но все они очень чувствительны к изменениям содержимого и длине сравниваемых слов. Например:
Скорость выполнения работы алгоритмов нечеткого поиска обычно напрямую зависит от размера словаря. Но, модификации и доработки этих алгоритмов позволяют добиться достаточного малого времени работы даже при весьма больших объемах словарей.
Выводы
В результате проведенного обзора актуальных методов и алгоритмов нечеткого поиска, были отмечены достоинства и недоставки этих методов.
Также, выделим алгоритмы с индексацией. Они имеют сложную реализацию, а также требуют подготовленный словарь для сравнений, но, значительно быстрее выполняют сравнение строк большой размерности, а также более точно определяют схожесть этих строк. Данные алгоритмы с их модификацией наиболее подойдут для реализации поставленных задач в пределах исследуемой области.
Литература