Перевод Моргун И.С. - Ilya Ilyankou Алгоритм сопоставления с образцом Ratcliff / Obershelp

Алгоритм сопоставления с образцом Ratcliff / Obershelp

Алгоритм сопоставления с образцом Ratcliff / Obershelp был представлен Джоном У. Рэтклиффом и Джон А. Обершельп в 1983 году. Этот алгоритм оказал влияние на промышленность образовательное программное обеспечение.

Ранее образовательное программное обеспечение часто предлагало только тесты с множественным выбором, как для алгоритмы типизированных ответов пользователей для обработки и проверки введенных данных были необходимы.

Например, на вопрос, кем был египетский фараон 18-й династии, ответы Тутанхамона, Тутенхамона, Тутанхамона, Тутанхамона должны быть считается правильным. Кроме того, пользователь мог ввести двойной «м» или сделать другой вид опечатки.

Алгоритм Ratcliff / Obershelp помог решить эту проблему. Как яро-винклер В алгоритме расстояния Ratcliff / Obershelp возвращает значение от 0 до 1, где 1 - это полное совпадение для двух заданных строк.

Km число совпадающих символов,
|S1| and |S2| длина сравнивающихся слов

Пример

Найдем сходство между строк MATHEMATICS и MATHEMATICA.

Первая строка имеет длину |S1| = 11, а вторая |S2| = 10.

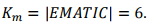
Далее, определяем саму длинную подстроку, которая содержится в обоих строках, - EMATIC. Длина этой подстроки равна формула поиска метрики

Слева от самой длинной подстроки остались наборы символов MATH и MAT. Самая длинная общая подстрока - MAT. Следовательно,

Поскольку подстрока MAT является началом обеих строк S1 и S2, нет символов слева от него. Справа от MAT, в строке S1 имеем символ H, а в строке S2 их нет. Поэтому остается неизменным и мы идем к символам справа от EMATIC.

Справа от EMATIC есть символы S (в S1) и A (в S2) слева. Но они не совпадают, так как разные. Таким образом, значение остается 9 и все символы в обеих строках S1 и S2. У нас есть все данные для вычисления показателя Ратклиффа/Обершелпа.

Мера сходства Ратклиффа/Обершелпа для строк MATHEMATICS and MATEMATICA: