Метод моделирования алгоритмов резервного копирования для получения оценок объема репозитория

УПРАВЛЕНИЕ И ПОДГОТОВКА КАДРОВ ДЛЯ ОТРАСЛИ ИНФОКОММУНИКАЦИЙ

Том 6, № 3, 2008

УДК 001.57:519.876.5:004.942

МЕТОД МОДЕЛИРОВАНИЯ АЛГОРИТМОВ РЕЗЕРВНОГО КОПИРОВАНИЯ ДЛЯ ПОЛУЧЕНИЯ ОЦЕНОК ОБЪЕМА РЕПОЗИТОРИЯ

Казаков В.Г., Федосин С.А

В работе представлен метод математического моделирования алгоритмов резервного копирования, который дает возможность получить аналитически оценку требуемого объема репозитория. Рассмотрены как традиционные алгоритмические подходы, так и нетривиальные. Представлены результаты экспериментов, дающих оценку применимости метода. Описанный метод незаменим при проектировании новых схем резервного копирования, также пригоден для построения системы прогнозирования для современных систем резервного копирования.

Введение

Вместе с быстрым ростом объемов хранимых данных возрастает сложность их защиты, используя традиционные алгоритмы резервного копирования [1]. Каждый алгоритм резервного копирования делает компромисс между характеристиками процессов создания копий и операций восстановления данных [2]. При разработке новых схем резервного копирования, а также при построении аппарата прогнозирования систем резервного копирования требуется инструмент для априорной аналитической оценки того, сколько потребуется места для хранения резервных копий.

Постановка задачи

Рассмотрим некоторую систему резервного копирования, которая создает копии данных в последовательные запланированные моменты времени {tk, где k = 0; 1; 2 … T}. Систему данных для резервного копирования на момент времени tj ∈ tk обозначим как Dj. Будем отныне всегда предполагать, что начальное состояние данных D 0 – пустое, а D1 нет, то есть D0=Ø, D1≠Ø. Каждая сделанная копия данных сохраняется в некотором хранилище данных – репозитории. Каждую такую копию будем называть элементом репозитория. Элемент репозитория, который со держит изменения между состояниями данных с момента t l до момента tl+n, то есть от Dl до Dl+n, обозначим как , где l и n – целые, причем n > 0, l ≥ 0. Учитывая, что начальное состояние данных пустое, фактически означает полную резервную копию состояния данных в момент tn, то есть копию Dn.

Имеет смысл операция объединения элементов репозитория. Например, объединяя полную резервную копию системы данных на момент tl, то есть , с элементом репозитория, содержащим изменения между состояниями данных c момента времени tl до момента tl+n, то есть c , мы получаем полную резервную копию системы данных на момент tl+n, то есть .Следует заметить, что не все элементы могут быть объединены друг с другом, нет смысла, например, объединять элементы, содержащие изменения данных в непоследовательные периоды времени. Для объединения несочетаемых элементов репозитория введем элемент X, который будет обозначать некий «испорченный» элемент. Множество всех элементов репозитория обозначим Rep. Rep включает в себя все возможные элементы репозитория и введенный «испорченный» элемент X:

Rep = {X; Rij}i=0,1,2...; j=1,2,3... ={X; ; ; ;...; ; ; ;...; ; ; ;...}.

Операцию объединения элементов репозитория ⊕ на множестве всех элементов репозитория Rep введем следующим образом:

1. X ⊕ X = X; c ⊕ X = X ⊕ c = X;

2. ⊕=.

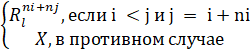Заметим, что введенный способ объединять элементы репозитория является алгебраической бинарной ассоциативной операцией, а множество всех элементов репозитория с операцией объединения элементов репозитория, то есть Rep⊕, является полугруппой.

При моделировании алгоритмов резервного копирования требуется построить схему создаваемых элементов репозитория в общем виде. Для получения количественных характеристик объема репозитория на заданный момент времени необходимо в соответствии с определенными предположениями о характере роста и изменении резервируемых данных построить функцию, ставящую в соответствие каждому создаваемому элементу репозитория действительное число, обозначающее его объем.

Моделирование алгоритмов резервного копирования

Рассмотрим различные алгоритмические подходы в системах резервного копирования, запишем для каждого общий вид, необходимый для дальнейшего количественного анализа.

Полное резервное копирование

Процесс резервирования включает копирование всех файлов и папок, выбранных для резервного копирования вне зависимости от того, изменились они или нет, в каждый момент резервирования tj∈tk,, как показано на рис. 1.

Определение. Алгоритм резервного копирования, в процессе работы которого последовательно в моменты времени {tk, где k = 0; 1; 2 …T} создается набор элементов репозитория вида R = {; ; ;...; }, называется алгоритмом полного резервного копирования.

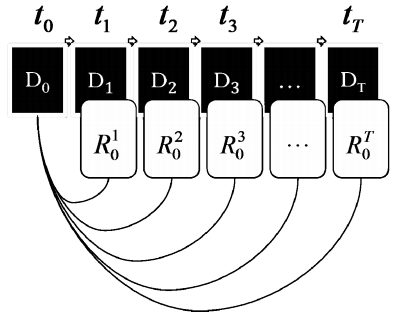
Рис. 1. Полное резервное копирование

Инкрементное резервное копирование

Изначально, в момент времени t1 создается полная резервная копия данных , а затем, в последующие моменты, создаются копии файлов, измененных с момента последнего резервирования. Рис. 2 иллюстрирует данную схему.

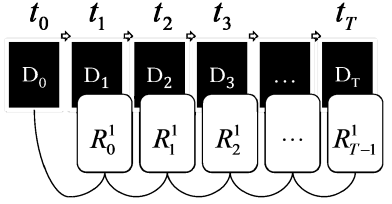
Рис. 2. Инкрементное резервное копирование

Дифференциальное резервное копирование

При дифференциальном резервировании изначально, в момент времени t1 создается полная резервная копия данных , а затем, в последующие моменты, создаются копии, содержащие каждый файл, который был изменен с момента последнего полного резервирования (рис. 3).

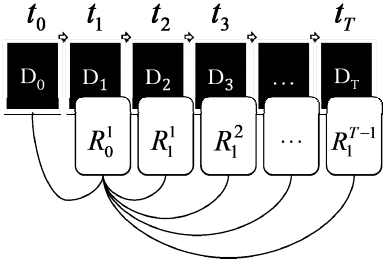
Рис. 3. Дифференциальное резервное копирование

Мультиуровневое резервное копирование

Мультиуровневая схема (multi-level backup) работает таким образом - резервное копирование ведется в несколько уровней: на 0-ом уровне создаются полные резервные копии; на последующих – копируются файлы, модифицированные с момента предыдущего резервного копирования более низкого уровня.

Определение. Алгоритм резервного копирования, в процессе работы которого последовательно в моменты времени {tk, где k = 0; 1; 2 … T} создается набор элементов репозитория вида (1), называется мультиуровневой схемой для количества уровней L равного l + 1, и где для каждого i-го уровня создается ni элементов репозитория:

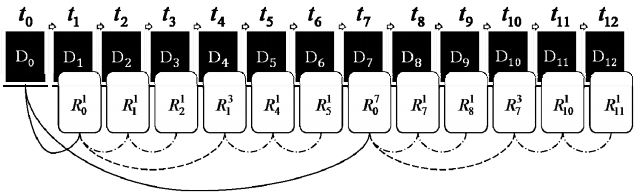
Рис. 4. Мультиуровневое резервное копирование

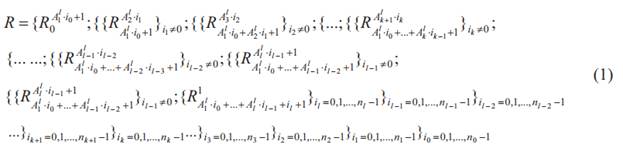
,где {}условное выражение истинно = {}; {}условное выражение ложно = Ø.

На рис. 4 представлена иллюстрация работы алгоритма мультиуровневой схемы для следующих параметров: L = 3, n0 = 2, n1 = 2, n2 = 2, T = 12. Сплошными линиями на рисунке обозначены операции резервного копирования нулевого уровня, пунктиром – первого, пунктиром с точками – второго.

Схема Костелло, Юманса, Ву

Резервное копирование при работе данного алгоритма ведется параллельно, в несколько уровней. В результате создается совокупность L наборов элементов репозитория. На нулевом уровне создание резервных копий идентично инкрементной схеме. Все прочие уровни избыточны – создаются для увеличения скорости восстановления (см. [3]).

Определение. Алгоритм резервного копирования, в процессе работы которого последовательно в моменты времени {tk, где k = 0; 1; 2 …T} создается набор элементов репозитория вида (2), является схемой Костелло, Юманса, Ву (далее в обозначениях – WCU), где b – параметр схемы – «база» (base).

На рис. 5 представлена иллюстрация схемы для следующих параметров: L = 3, b = 2, T = 12.

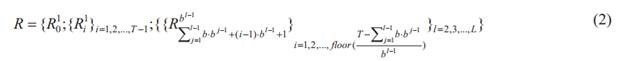
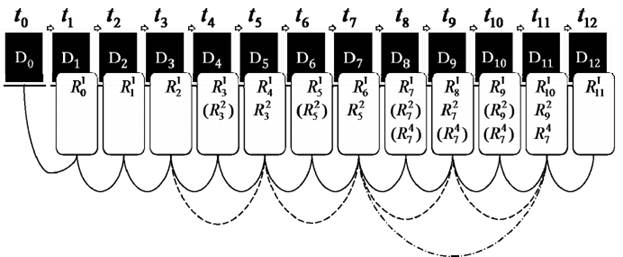
Рис. 5. Резервное копирование схемы Костелло, Юманса, Ву

Частичное создание на рис. 5 обозначено элементами репозитория в скобках.

Алгоритм резервного копирования «Z scheme» «Z scheme» осуществляет параллельные операции резервного копирования также в несколько потоков, в результате создается совокупность L наборов элементов репозитория. На нулевом уровне создание резервных копий идентично инкрементной схеме. Все прочие уровни избыточны – создаются для увеличения скорости восстановления (см.[4]).

Определение. Алгоритм резервного копирования, в процессе работы которого последовательно в моменты времени {tk, где k = 0; 1; 2 …T}

создается набор элементов репозитория вида называется алгоритмом резервного копирования «Z scheme». На рис. 6 представлена частичная иллюстрация алгоритма резервного копирования «Z scheme» для следующих параметров: L = 4, b = 2, T = 12. Пунктирные линии означают исключение из создаваемого элемента репозитория изменений, относящихся к указываемому пунктиром периоду.

Получение количественных характеристик моделируемых алгоритмов

Для того чтобы получить количественные характеристики объема репозитория, требуемого для хранения создаваемых элементов репозитория, необходимо каждому элементу репозитория поставить в соответствие некоторое действительное число, обозначающее его объем. Для этого необходимо ввести предположения о характере изменения данных для резервного копирования во времени.

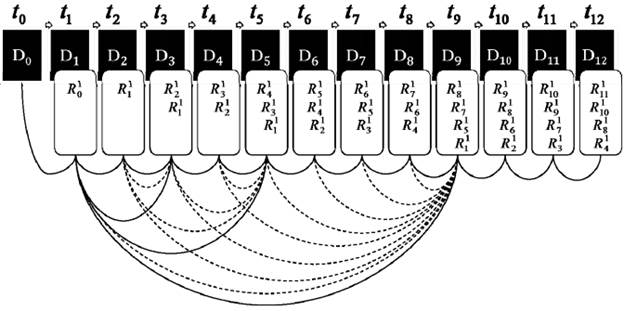
Рис. 6. Резервное копирование схемы «Z scheme»

Итак, предположим, что объем данных D1 равен V1∈R+. Предположим также, что между двумя любыми последовательными моментами времени, когда создаются резервные копии, данные увеличиваются на некоторую постоянную вели чину так, что объем Dl , l > 0 равен V1 + p·V1·(l – 1),где p будем называть коэффициентом увеличения данных.

Предположим теперь, что между двумя любыми последовательными моментами времени, когда создаются резервные копии, данные изменяются на некоторую величину так, что объем из менений между Dl и Dl+1 равен d(V1(1+p(l-1)). Названный объем изменений не включает добавляемую часть. В дальнейшем d будем называть коэффициентом изменения данных. Такие предположения о характере изменения данных соответствуют статистике накопления данных в реальных системах, что можно проследить по данным исследований, например, компании Teradactyl LLC, занимающейся разработкой систем резервного копирования [5], и по данным исследований, проведенных в Технологическом Институте в Джорджии, США[2].

Нужно заметить, что каждый алгоритм резервного копирования в построенных моделях будет давать несколько меньшие значения, что объясняется отсутствием учета при моделировании наличия служебной информации, необходимой в реальных системах резервного копирования для

работы. Чтобы компенсировать это, необходимо ввести корректирующий коэффициент, отражающий объем служебных данных.

Введем функцию vols: Rep → R+, которая будет ставить в соответствие каждому элементу репозитория положительное действительное число, обозначающее объем требуемой памяти для хранения этого элемента. Значение функции складывается из объема прибавленных данных Θприб., объема измененных данных Θизм. и объема служебных данных Θслужебн. за промежуток, соответствующий аргументу, то есть vols = Θприб. + Θизм. + Θслужебн..

Рассмотрим некий элемент репозитория , тогда vols() = Θприб. () + Θизм. () + Θслужебн.. ().

Объем прибавленных данных Θприб. и объем измененных данных Θизм. с учетом наших предположений выражают формулы (3). Случай, когда l = 0, выделяется отдельно из-за предположения, что начальное состояние данных пустое, а последующее за ним нет, поэтому в этих случаях элемент объем измененных данных также пуст, а объем прибавленных данных включает начальный объем V1.

Объем служебных данных Θслужебн. зависит прежде всего от конкретной реализации системы резервного копирования и требует моделирования в каждом отдельном случае. Однако невозможно пренебречь учетом данной составляющей, ибо в отдельных случаях доля служебных данных может составлять десятки процентов в совокупном объеме репозитория.

В результате получим функцию vols, определяемую (4).

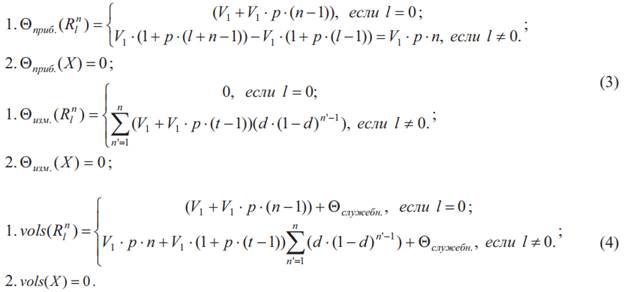
В результате работы схемы резервного копирования создаются наборы элементов репозитория. Используя приведенные выше записи алгоритмов в общем виде, мы можем составить совокупность хранимых элементов репозитория на каждый момент времени tj∈tk. Далее, поставив в соответствие каждому элементу репозитория число, обозначающее его объем, и просуммировав их все, мы получим оценку места, требуемого для хранения резервных копий, необходимого для работы рассматриваемой схемы резервного копирования.

Сопоставление модельных данных с экспериментальными

Используя описанный аппарат, были построены модели для каждой рассмотренной схемы и получены количественные характеристики.

Изначально аналитически полученные результаты были сопоставлены с данными экспериментов, проведенных в Университете Мериленда в Балтиморе, США[2], где испытывался прототип реальной системы резервного копирования в реальных условиях, результаты которых представлены на рис. 8. В модели были заданы идентичное начальное состояние данных, коэффициенты роста и изменения объема данных. Анализ показал, что получаемые данные адекватны данным рассмотренного эксперимента.

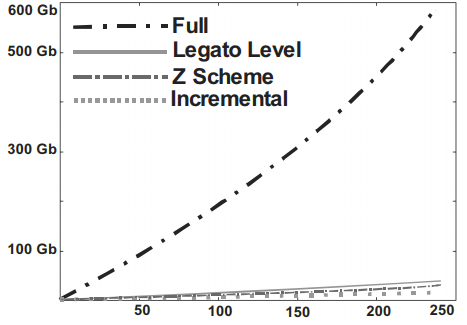
Рис. 7. Изменение объема репозитория

Для более детальной проверки правильности получаемых аналитически данных был разработан программный прототип системы резервного копирования, реализующий все рассматриваемые схемы резервного копирования, где были произведены все необходимые испытания.

В разработанной системе резервного копирования предусмотрено хранение следующей служебной информации: файлового индекса системы резервируемых данных на каждый момент создания резервных копий; список элементарных операций, производимых в каждый момент резервного копирования; другие данные, объем которых не превосходит 0,01% от общего объема служебных данных. Объем файлового индекса линейно зависит от объема файловой структуры системы резервируемых данных. Список элементарных операций линейно зависит от объема копируемых изменений.

Используя известные предположения о характере роста и изменения данных, а также выяснив объем записей в создаваемых индексах и списках, была построена модель объема служебных данных с максимальным отклонением менее 3,47% и средним отклонением 1,18% по всем проведенным испытаниям.

В целом, анализ получаемых результатов сопоставления показал довольно высокую точность аналитических данных. В частности, рассмотрим результаты экспериментов со следующими параметрами: начальное состояние данных V1 = 1610612736 (1,5 Гб), коэффициенты роста p = 0,5% и изменения объема данных d = 0,2%. Данные были собраны за 365 периодов резервного копирования (эмуляция одного года с ежедневным резервным копированием). На рис. 8-9 отображены данные, полученные аналитически. На рис. 9 отдельно отображены алгоритмы мультиуровневой схемы, схемы Костелло, Юманса, Ву, «Z scheme», инкрементного копирования в более детализированном виде.

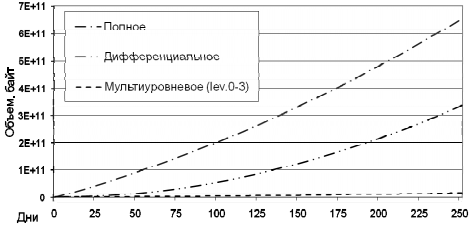
Рис. 8. Изменение объема репозитория

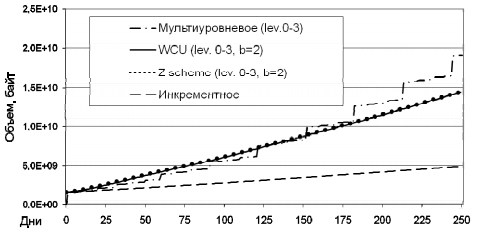
Рис. 9. Изменение объема репозитория

Точность аппроксимации в модели реальных данных для резервного копирования составляла в среднем 0,01% на каждом шаге. Наиболее чувствительны к точности аппроксимации схемы, где много элементов репозитория ( Rln ), объединяющих изменения за несколько периодов, то есть с большими значениями параметра n и ненулевым l, ибо в этом случае имеет место накопление ошибки. Так, например, при работе дифференциальной схемы параметр n постоянно увеличивается, этим и объясняется наименьшая точность среди других рассмотренных алгоритмов.

В среднем отклонение модельных от экспериментальных данных по всем экспериментам составило 0,85%. Средние и максимальные отклонения для различных схем резервного копирования показаны в таблице 1.

Таблица 1. Отклонение модельных данных от экспериментальных

Тип резервного копирования	Среднее отклонение, %	Максимальное отклонение, %
Полное	0,47	0,78
Дифференциальное	1,26	1,47
Инкрементное	0,63	0,94
Мультиуровневое	1,00	1,27
WCU(lev. 0-4; b=2)	0,89	1,16
Z-Scheme (lev.0-4; b = 2)	0,83	0,98

Иллюстрация изменения отклонения в динамике представлена на рис. 10.

Выводы

Полученные результаты показали достаточную точность аналитических данных для применения описанного метода для построения оценок требуемого объема репозитория.

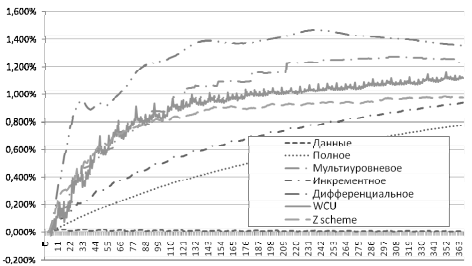
Рис. 10. Отклонение модельных данных от экспериментальных

Таким образом, данный метод создания аналитических оценок применим при проектировании новых схем резервного копирования, ибо помогает априорно аналитически оценивать одну из основных характеристик процессов резервирования – объем требуемого места для хранения. Таким образом, создаваемый алгоритм резервного копирования сначала исследуется в модели, затем уже реализуется программно и тестируется. Рассмотренный метод пригоден также для построения систем прогнозирования в современных системах резервного копирования.

Литература

1. Chervenak A.L., Vellanki V., Kurmas Z., Gup-ta V. Protecting File Systems: A Survey of Backup Techniques // Proc. Joint NASA and IEEE Mass Storage Conference, 1998. www.isi.edu/~annc/papers/mss98final.ps

2. Kurmas Z., Chervenak A. Evaluating backup algorithms // Proc. of the Eighth Goddard Con-ference on Mass Storage Systems and Tech-nologies, 2000. http://www.cis.gvsu.edu/~kurmasz/papers/ kurmas-MSS00.pdf

3. Costello A., Umans C., Wu F. Online backup and restore // Unpublished Class Project at UC Berkeley, 1998. http://www.nicemice.net/amc/research/backup/

4. Kurmas Z. Reasoning Behind the Z Scheme. 2002. http://www.cis.gvsu.edu/~kurmasz/Research /BackupResearch/rbzs.html

5. Teradactyl LLC. True Incremental Backup. 2007. http://www.teradactyl.com:80/Documents/BackupTypes/PartCumulativeIncr.html