Обобщение алгоритма Бута для эффективного умножения

Аннотация

В этой статье мы суммируем существующую работу по классическому алгоритму умножения Бута и предлагаем улучшенную версию его общего вида. В алгоритме Бута или модифицированном Буте в множителе учитываются одновременно два или три бита. Здесь мы показали подход с использованием любого количества бит умножителя. Затем находим оптимальное значение таких битов для которая сложность операции будет минимальной.

Введение

Умножение, процесс многократного сложения - одно из самых ранних достижений математики. Это коммутативно и распределительнно над сложением и вычитанием. Есть несколько вычислительных подходов для умножения. Два числа, подлежащие умножению, называются умножением и умножением. Таким образом, результат умножение - это число (произведение), которое будет получено путем сложения множителя с множителем. Алгоритм Бута умножает два двоичных числа со знаком в двоичном виде. Алгоритм был предложенный А. Д. Бутом в 1951 г. [1]. Бут работал с настольными калькуляторами, которые быстрее переключались, чем прибавляли, и он использовал операцию сдвига, чтобы создать свой быстрый алгоритм умножения. Этот алгоритм представляет интерес в исследовании компьютерной архитектуры. Алгоритм Бута основан на четырех шагах в двоичных числах. Пусть множимое, множитель и частное произведение обозначаться M, R и P. В процессе добавляется дополнительный 0 справа от самого младшего значащего бита (LSB) от M, и проверяются два бита умножителя из LSB, и в зависимости от их значений, R добавляется или вычитается от P. В конце каждого шага один бит множителя сдвигается вправо до нуля. Основные условия и действия следующие:

Модифицированный алгоритм Бута был разработан для трех битов и основан на восьми условиях. Операции выполняются на двоичных числах. Три бита множителя проверяются и на основании их значений, операции выполненяются. В начале процесса один дополнительный 0 добавляется справа от LSB от M и множитель сдвигается дважды вправо в конце каждого шага, пока не станет 0. Восемь условий и действий

Существуют некоторые статьи по модифицированному алгоритму Бута [1], в которых использовался множитель в основаниях с более высокой (> 3) степенью двойки. Но с увеличением степени скорость получения неправильных результатов увеличивается. Коррекция на продукт необходима для точных результатов. Эти изменения необходимы в основном для умножения действительных чисел.

Основная идея:

Мы сделали обобщение алгоритма Бута [4] для любой степени двойки, что является точным и эффективным. Чтобы развить это, мы отметили, что количество требуемых сдвигов частичного произведения на единицу меньше числа битов, сравниваемых на каждом шаге; то есть, если число битов умножителя равно m, то число сдвига, необходимое для выполнения с частичным произведением, равно m-1. Общее количество возможных битовых комбинаций - 2 в степени m. В алгоритме Бута общая комбинация битов умножителя может быть разделена на две части, каждая часть с числом (2 в степени m)/ 2 = 2m − 1. Все возможные операции для одной части одинаковы для другой, но противоположны; то есть одна часть является дополнением 1 к другой. Если общее количество рассматриваемых битов равно m, то числа начинаются с m 0c и заканчиваются m 1с. Таким образом, если мы разделим все возможные комбинации на две части, то наибольшее число в первой части будет равным всем 1 в комбинации битов, кроме старшего значащего бита (MSB). В качестве примера рассмотрим следующие числа для m бит

0000… 00 // m число 0, начало первой части
0000 ... 01
0000 ... 10
,
,
,
,
0111… 11 // конец первой части
1000… 00 // начало второй части
1000 ... 01
1000 ... 10
1000 ... 11
,
,
,
,
1111… 11 // м число 1 с, конец второй части

Если нам нужно вычислить обобщенный алгоритм Бута для множителя m битов, то выполняемые операции; то есть число мультипликатов, которые должны быть добавлены к частичному продукту, является следующим:

+ 0 * R // начало первой части
+ 1 * Р
+ 1 * Р
+ 2 * R
+ 2 * R
,
,
,
+ (Т-1) * Р
+ (Т-1) * Р
+ m * R // конец первой части
-m * R // начало второй части
- (м-1) * Р
- (м - 1) * р
,
,
,
-2 * Р
-2 * Р
-1 * Р
-1 * Р
-0 * R // конец второй части

В приведенном выше примере работа одной части аналогична другой, но противоположна другой. Максимальный множитель, который будет добавлен, равен m; то есть количество битов умножителя, которые следует учитывать. Итак, в целом можно сказать следующее:

Для m бит возможная комбинация будет от 0 до 2^m-1, первая часть будет от 0 до 2^m-1, а вторая часть будет от 2^m-1 до 2^m-1, и для этих чисел выполняемые операции будут соответственно для i = 1 до 2m + j * i ?для первой части? и i = 2m до 1 - j * i для второй части, где j = 1/2.

Алгоритмическая форма

Вышеуказанный процесс является обобщенной формой классического алгоритма умножения Бута. В алгоритме Бута и Модифицированного Бута число битов умножителя равно двум и трем соответственно. В этом процессе количество битов может быть любым числом n. Пусть множитель будет R, а множимое M и количество битов, которые будут считаться, будут n, а общее число битов умножителя будет N, а частичное произведение умножения будет A. Предлагаемая алгоритмическая форма выглядит следующим образом:
1. Проверьте биты множителя. Если MSB равен 1, тогда возьмите дополнение 1 битов умножителя, скажем,M. Если нечетно, то добавьте 1, чтобы сделать M+1. Теперь вычтите (M+1) / 2 * R из частичного произведения, если M нечетное. Если четное, то вычтите M/ 2 * R из частичного произведения; то есть вычислить

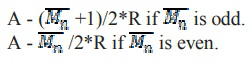
2. Проверьте биты множителя. Если MSB равен 0, а бит множителя равен четному (M), то добавьте M/ 2 * R к частичному произведению. Если бит множителя нечетный (M), то прибавьте (M+1) / 2 * R к частичному произведению; то есть вычислить

Расчет количества частичных произведений:

Здесь необходимо упомянуть, что если общее количество битов в множителе равно n, а количество рассматриваемых битов равно m, то общее количество проходов P будет равно:

I. P = n / (m-1), если n равномерно разделено на (m-1)
II. P = n / (m-1) + 1. В противном случае

Графическое представление алгоритма:

Приведем пример множителя длиной 25 бит. Следующая таблица (Рисунок 1) представляет количество частичных произведений по отношению к разному количеству бит умножителя, которое следует учитывать при умножении. Из таблицы видно, что когда число битов мало, частичные произведения велики, но с увеличением значения битов количество частичных произведений уменьшается.

Чтобы наблюдать скорость изменения частичного продукта, следующий график (рисунок 2) взят из таблицы 1. Здесь ось X представляет количество битов множителя, который необходимо рассмотреть, а ось Y представляет количество частичных произведений. Синяя линия представляет количество битов умножителя, а красная представляет количество частичных произведений для определенного множителя. Здесь отметим, что после определенного значения множителя бит частичное произведение насыщается. Следовательно, мы должны заметить, что с увеличением количества битов умножителя накладные расходы на операцию на каждом шаге увеличиваются. Здесь пересечение синей и красной линии представляет оптимальное значение рассматриваемого бита множителя, для которого необходимая операция также является оптимальной. Отметим, что количество битов, равное 4, и количество частичных произведений, равное 7, дает оптимальное значение. Здесь следует отметить, что это особый случай. Оптимальное значение битов умножителя изменяется каждый раз с изменением длины битов умножителя.

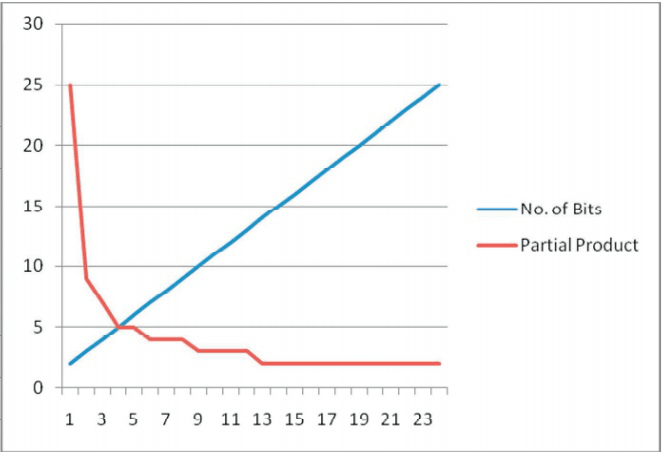
Рисунок 1 - График для радикального частичного результата

Рабочий пример

Давайте проиллюстрируем наш подход на примере. Здесь мы берем большой множитель и маленький множитель, чтобы показать выигрыш в сложности алгоритма. Таким образом, мы имеем
М = 1485 = 10110011011101 (в двоичной записи)
R = 5 = 101 (в двоичной записи)
Здесь n = 14 и m = 4
Тогда согласно нашему подходу
Шаг 1 +1111111111110001 // - 3 * 5
Шаг 2 +0000000010100 *** // + 4 * 5
Шаг 3 +0000001111 ****** // + 3 * 5
Шаг 4 +1110110 ********* // - 2 * 5
Шаг 5 +1111 ************ // + 3 * 5
Результат = 1110000001010001 // 11485 * 5 = 57425
Итак, мы получили правильный результат. По правилам P = 4.

Сравнение между Бутом, Модифицированным Бутом и Предлагаемым процессом.

В предлагаемом подходе мы видели, что с различным коэффициентом умножения умножение может быть выполнено, тогда как в процессе Бута использовалось основание, равное двум или трем. Поэтому наш процесс является более гибким по сравнению с алгоритмом Бута и Модифицированного Бута.

Таблица 2: сравнение между Бутом, Модифицированным Бутом и предлагаемым подходом.

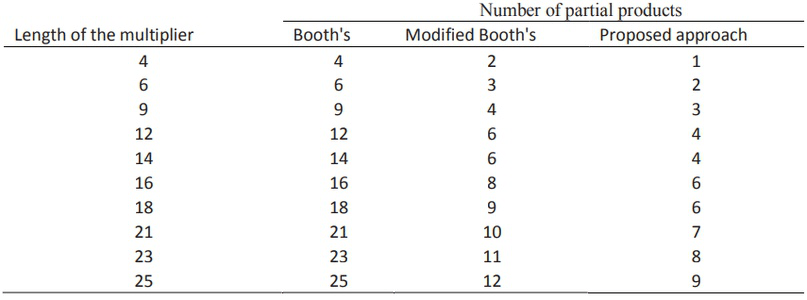
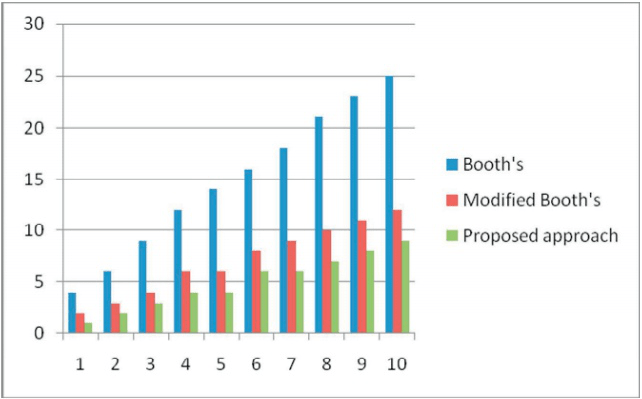
График для различных частичных произведений для фиксированной длины множителя

Заключение:

Подход для умножения двух чисел был описан в целом на основе классического алгоритма Бута. Здесь нам не нужно беспокоиться о количестве битов умножителя. Этот подход более эффективен, чем несколько подходов умножения [2] [3] [4]. Мы отметили, что для данного количества бит умножителя операции, требуемые нашим подходом, являются самыми низкими среди этих подходов.

Список литературы

1. [1] A. Booth, “A signed binary multiplication technique,” Q. J. Me& Appl. March., vol. 4, pp. 236-240, 19.51
2. [2] John P. Hayes “Computer architecture and organization”, Second Edition, McGraw-Hill, 1988
3. [1] M. Morris Mano “Computer System Architecture”, Third Addition, Prentice Hall, 1993.
4. [2] Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullmant “The design and analysis of computer algorithm” Pearson, 1974.
5. [3] Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullmant “The design and analysis of computer algorithm” Pearson, 1974.
6. [4] Phil E. Madrid, Brian Millar and Earl E. Swartzlander, Jr, “Modified Booth’s algorithm for high radix fixed point multiplication”, IEEE Transactions on Very Large Scale Integration (VLSI) Systems , Vol. 1, No. 2 June 1993