Савкин В.Ю., Светличная В.А. – Анализ методов решения задачи коммивояжёра

Авторы: Савкин В.Ю., Светличная В.А.
Источник: Информатика, управляющие системы, математическое и компьютерное моделирование (ИУСМКМ – 2018) / Материалы IX международной научно–технической конференции – Донецк: ДонНТУ, 2018г. – с. 6–10.

Аннотация

Савкин В.Ю., Светличная В.А. Исследование задачи коммивояжёра и методов её решения. В данной статье описаны основные задачи транспортной логистики, одной из которых является задача коммивояжёра. Приведена математическая постановка задачи коммивояжёра. Определены критерии оптимизации маршрута доставки и ограничения, влияющие на формирование маршрута. Исследованы методы и алгоритмы, которые применялись для решения этой задачи.

Annotation

Vladyslav Savkin, Victoria Svetlichnaya. Investigation of the traveling salesman problem and methods of it solution. This article describes the main tasks of transport logistics, one of which is the traveling salesman problem. A mathematical statement of the traveling salesman problem is given. The criteria for the optimization of the delivery route and the restrictions affecting the formation of the route are determined. The methods and algorithms that were used to solve this problem were investigated.

Введение.

Транспортная логистика – это комплекс мероприятий, осуществляемый с целью организации доставки товаров и грузов с минимальными временными и финансовыми затратами [1]. Транспортную логистику можно представить в виде шести последовательных задач, таким образом к каждой из этих задач можно приступить только после выполнения предыдущей. Этими задачами являются:

учёт наличия товаров на складе – регистрация товара на складе c информацией о текущем остатке;
учёт и обработка заявок на поставку товара – сбор заявок на доставку товаров со всех пунктов и последующее формирование одной единой заявки;
расчёт загрузки транспортных средств – вычисление необходимого количества грузовых автомобилей для транспортировки всех товаров из общей заявки с учётом параметров груза (длина, ширина, высота, общая масса тары) и автомобилей (грузоподъёмность автомобиля, длина, ширина и высота контейнера или отсека);
разбиение обрабатываемого участка на геозоны (кластеры) с учётом имеющегося транспорта – задача кластеризации;
построение наиболее выгодного маршрута доставки товара задача коммивояжёра;
комплектование контейнера автомобиля таким образом, чтобы по прибытии в каждый пункт доставки груз, предназначенный конкретно для текущего пункта, находился ближе остальных по отношению к началу контейнера – задача о рюкзаке.

Задача коммивояжёра является лишь одним из элементов транспортной логистики и для неё существуют как предшествующие, так и последующие задачи.

Цель исследования.

Целью исследования задачи коммивояжёра является определение таких параметров, характеристик и алгоритмов, которые смогли бы удовлетворить условию поиска оптимального маршрута для большого количества вершин, т.е., по сути, нахождение оптимального решения этой задачи. Для этого необходимо выполнить ряд следующих подзадач:

определить ограничения, влияющие на маршрут;
представить задачу коммивояжёра математическим способом;
определить критерии оптимальности маршрута;
определить наиболее эффективный алгоритм для решения задачи.

Постановка задачи.

Задача коммивояжёра представляет собой задачу поиска кратчайшего Гамильтонова пути в полном конечном графе с N вершинами [2]. Коммивояжёр, выходящий из какого-нибудь пункта, желает посетить N-1 других пунктов и вернуться к исходному пункту. Известны расстояния между всеми этими пунктами. Требуется установить, в каком порядке он должен посещать эти пункты, чтобы маршрут можно было считать оптимальным исходя из выбранного критерия.

На процесс формирования оптимального маршрута может влиять ряд дополнительных факторов, которые принято называть ограничениями. Для задачи коммивояжёра ограничениями являются:

количество автомобилей, выполняющих транспортировку груза, равное количеству кластеров (геозон);
список заявок на доставку груза, сформированных по каждому пункту доставки.

Постановка задачи для одного маршрута звучит следующим образом. Имеется n пунктов, стоимость между которыми задана матрицей C. Коммивояжёр должен побывать в каждом пункте один раз и вернуться в исходный пункт маршрута, затратив при этом минимум средств [3]. Математически это может быть представлено следующей формулой, которая также представляет собой целевую функцию:

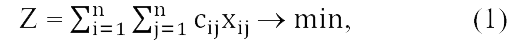
где n – количество пунктов на карте;

c_ij – матрица стоимости между пунктами;

x_ij – матрица переходов с компонентами:

x_ij = 1, если маршрут включает переезд из точки i непосредственно в точку j;

x_ij = 0, в противном случае.

Аналитическую постановку задачи можно сформулировать следующим образом: найти минимум функции Z при выполнении ограничений и неотрицательности значений матрицы X [4]. Систему ограничений можно представить следующим образом:

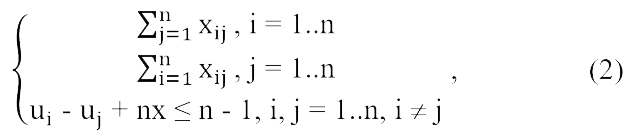
где n – количество пунктов на карте;

x_ij – матрица переходов с компонентами:

u_i, u_j – произвольные целые неотрицательные числа.

При этом каждое из ограничений выражает следующие условия:

ограничение №1 выражает условие, что коммивояжёр выезжает из каждого пункта один раз;
ограничение №2 выражает условие, что коммивояжёр въезжает один раз в каждый пункт;
ограничение №3 выражает условие, что маршрут не будет содержать в себе замкнутые маршруты (условие незамкнутости), кроме одного, включающего все пункты, а также то, что маршрут не должен содержать петель.

Маршрут можно считать оптимальным исходя из следующих критериев:

наименее затратный маршрут с точки зрения времени или расстояния;
наименее затратный маршрут с точки зрения финансовой составляющей;
наименее затратный маршрут с точки зрения времени, расстояния, и финансовой составляющей, т.е. совокупный критерий.

Стоит отметить, что кратчайший маршрут не всегда является наименее затратным, поэтому эти два критерия стоит рассматривать как отдельные.

Обзор методов и алгоритмов.

Для решения задачи коммивояжёра существует довольно большое количество методов и алгоритмов, каждый из которых отличается собственной особенностью реализации и может решать задачу как целиком, так и её отдельные подзадачи. Эти алгоритмы и методы можно классифицировать как точные, эвристические и поисковые.

Точные алгоритмы. Среди точных алгоритмов наиболее популярными для решения задачи коммивояжёра являются:

метод последовательной сепарации [3];
алгоритм полного перебора [5];
метод ветвей и границ.

К преимуществам точных алгоритмов можно отнести возможность распараллеливания и точное решение задачи.

Эвристические алгоритмы. Эвристические алгоритмы эффективны как при решении обобщённой задачи коммивояжёра, так и при решении простой задачи коммивояжёра. К ним можно отнести довольно большое количество методов и алгоритмов:

нейронные сети [2];
BV-метод [5];
метод включения дальнего;
метод имитации отжига [6];
метод ближайшего соседа;
алгоритм разрезания общего маршрута;
алгоритм разделения по углу;
метод дихотомического разделения на группы;

Эвристические алгоритмы имеют линейную сложность, дают приблизительное решение задачи и в большинстве своём не поддаются распараллеливанию [5]. В некоторых случаях распараллеливанию поддаются только конкретные этапы алгоритма.

Поисковые алгоритмы. Поисковые алгоритмы являются наиболее распространёнными среди алгоритмов для решения задачи коммивояжёра. Лидерами среди них являются генетические алгоритмы и алгоритмы колонии муравьёв, или муравьиные алгоритмы [5].

Генетические алгоритмы являются наиболее оптимальными среди поисковых в плане соотношения время/качество и могут быть распараллелены.

Муравьиные алгоритмы наиболее эффективны для решения задачи коммивояжёра в плане конечного результата. Кроме того, для небольшого количества вершин задача может быть решена полным перебором, при увеличении числа вершин, когда задача становится NP-трудной, эффективность алгоритма возрастает. Стоит отметить, что муравьиные алгоритмы хорошо поддаются распараллеливанию.

Результаты сравнения.

Сведём результаты сравнения методов и алгоритмов в таблицы, характеризующие временные затраты и процент погрешности каждого метода. Сравнительный анализ всех классов алгоритмов представлен в таблицах 1-2 [7].

Таблица 1 – Относительная погрешность методов, %

Кол-во вершин, N	Точные алгоритмы		Эвристические алгоритмы		Алгоритмы поиска
Кол-во вершин, N	АПП	МВиГр	МВД	BV	ГА	Ant
20	0,05	0,09	7,99	5,37	2,85	0,78
40	0,2	0,34	11,56	8,76	3,54	2,04
60	0,37	0,68	13,18	10,03	3,81	1,89
80	0,66	0,81	13,89	11,16	5,27	1,81
100	0,79	1,09	14,04	11,42	5,05	2,03

Таблица 2 – Временные затраты методов, мс

Кол-во вершин, N	Точные алгоритмы		Эвристические алгоритмы		Алгоритмы поиска
Кол-во вершин, N	АПП	МВиГр	МВД	BV	ГА	Ant
20	16560	5881	7	25	245	104
40	618855	557798	10	84	740	924
60	54481312	19451803	20	401	1954	3603
80	-	-	57	918	4130	10342
100	-	-	110	2856	7139	22230

Обозначения. - – решение не было найдено за приемлемое (8ч) время.

Точные алгоритмы и методы дают точное решение, соответственно их погрешность минимальна, они могут быть распараллелены, что является важным фактором. Однако, большинство сфер, в которых может применяться задача коммивояжёра, требуют регулярного составления новых маршрутов, т.к. происходит ежедневное изменение пунктов доставки товара и их количества (как правило, значительно превышающее 10 единиц). Исходя из этого, временные затраты точных алгоритмов делают их непригодными для решения задач с большим количеством вершин [5]. Следовательно, можно сделать вывод о том, что данные алгоритмы и методы применимы только к задачам малого масштаба, в которых число пунктов доставки не превышает десяти.

Эвристические алгоритмы и методы являются лидерами по быстродействию, соответственно скорость их работы не требует больших вычислительных ресурсов, однако они дают лишь приблизительное решение задачи, т.е. погрешность при их использовании достаточно велика. Кроме того, эвристические алгоритмы далеко не всегда поддаются распараллеливанию – в некоторых случаях распараллелить можно лишь конкретные этапы алгоритма, в других случаях вообще невозможно применить параллелизм при их использовании. Следовательно, применение эвристических алгоритмов для решения рассматриваемой задачи актуально лишь в том случае, когда быстродействие является критичным параметром.

Поисковые алгоритмы являются компромиссным решением между точными и эвристическими – результативность поисковых алгоритмов является более чем удовлетворительной, т.к. в случае их использования и погрешность, и время выполнения стремятся к минимуму, в отличии от двух других классов алгоритмов, в которых оптимизации подлежит лишь один из вышеперечисленных критериев. При этом, поисковые алгоритмы достаточно чувствительны к параметрам, что может сказаться на конечном результате.

Исходя из результатов, можно сказать, что генетические алгоритмы дают более эффективный результат по сравнению с муравьиными. Однако, существует ряд скрытых факторов, которые могут негативно повлиять на конечный результат: высокие требования к вычислительным ресурсам, преждевременная сходимость, высокая чувствительность к параметрам и их неочевидная конфигурация, отсутствие эффективных критериев окончания работы алгоритма и т.д. [6].

В то же время, в работе муравьиных алгоритмов можно выделить такие особенности, как гибкость и возможность модификации n-го уровня [7]. Кроме того, муравьиные алгоритмы имеют преимущество перед генетическими алгоритмами и нейронными сетями – они опираются на память обо всей колонии вместо памяти только о предыдущем поколении, менее подвержены неоптимальным начальным решениям [8]. И не стоит забывать, что эффективность работы муравьиных алгоритмов возрастает с увеличением количества вершин, когда задача коммивояжёра становится NP-трудной.

Выводы.

С учётом всех вышеперечисленных факторов и проведённого исследования [9] [10], для решения задачи коммивояжёра наиболее целесообразно использовать муравьиные алгоритмы, которые были разработаны специально для решения данной задачи и являются наиболее эффективными в этой области. Однако, помимо самого алгоритма, нельзя забывать о критерии оптимизации, который указывает, в каком направлении должен работать алгоритм. Это важно с той точки зрения, что один и тот же алгоритм может давать разные результаты для разных критериев оптимизации при решении одной и той же задачи. Кроме того, стоит брать во внимание ограничения, которые будут влиять на работу алгоритма и конечный результат. Эти ограничения могут быть представлены в качестве входных данных.

Литература

Транспортная логистика [Электронный ресурс] – Режим доступа: [Ссылка]
Товстик, Т.М. Алгоритм приближённого решения задачи коммивояжёра / Т.М. Товстик, Е.В. Жукова // Вестник СПбГУ. – 2013. – №1. – С. 101-109.
Петрунин, С.В. Использование метода последовательной сепарации (ПС) для решения задачи коммивояжёра // Научный вестник МГТУ ГА. – 2009. – №143. – С. 87-90.
Задача коммивояжера. [Электронный ресурс] – Режим доступа: [Ссылка]
Борознов, В.О. Исследование решения задачи коммивояжёра // Вестник АГТУ. Сер: Управление, вычислительная техника и информатика. – 2009. – №2. – С.147-151.
Гараба, И.В. Сравнительный анализ методов решения задачи коммивояжёра для выбора маршрута прокладки кабеля кольцевой сети кольцевой архитектуры // Молодёжный научно-технический вестник. – 2013. – №1. С.173-188.
Решение сложных задач коммивояжера методами функциональных гибридных интеллектуальных систем / Под ред. А.В. Колесникова. – М.: ИПИ РАН, 2011. – 295 с., ил. – ISBN 978-5-902030-88-1
Семенкина, О.Е. Effectiveness Comparison of Ant Colony and Genetic algorithms for solving combinatorial optimization problems // Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева. – 2012. – №1. – С.96-97.
Курейчик, В.М. О некоторых модификациях муравьиного алгоритма / В.М. Курейчик, А.А. Кажаров // Известия ЮФУ. Технические науки. – 2009. – №1. – С.7-12.
Мурзин Б.П., Светличная В.А. Использование алгоритма муравьиной колонии для определения оптимального маршрута доставки грузов [Электронный ресурс] – Режим доступа: [Ссылка]

АНАЛИЗ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ КОММИВОЯЖЁРА