Автор: Цой Ю.Р., Спицын В.Г.
Источник: [Ссылка]
Аннотация
Актуальность исследований генетических алгоритмов (ГА) с динамически изменяемым размером популяции заключается в преимуществе, с точки зрения сложности алгоритма, адаптации размера популяции перед адаптацией других параметров ГА [Back et al, 2000]. Как правило, адаптация размера популяции осуществляется с использованием эвристических правил, созданных разработчиком, исходя из его личного опыта. В данной статье отражены результаты исследования ГА с постепенно изменяющимся размером популяции для решения задач численной оптимизации. Рассматриваются варианты ГА с различными стратегиями селекции и характеристиками оператора кроссовера. На основе полученных данных предлагается общий подход к изменению размера популяции. Формулируется ряд проблем, связанных с разработкой ГА с адаптивным размером популяции.
Введение
Несмотря на большой объем проведенных исследований, размер популяции в генетическом алгоритме (ГА) [Holland,
1975]
остается самым загадочным
параметром, потому что до сих пор неизвестно каким образом следует выбирать его
значение.
При этом оптимизация этого параметра способна дать больший прирост в скорости и эффективности, чем адаптация
генетических операторов [Back et al., 2000]. Несмотря на то, что есть результаты, позволяющие в определенных
случаях
вычислить размер популяции [Goldberg et al., 1992, Cvetkovic et al., 1994, Harik et al., 1997], получаемые
значения –
приблизительные и часто не соответствуют экспериментальным данным, либо требуют знаний о характеристиках
пространства
поиска и не учитывают влияние мутаций.
Во многих случаях количество особей в популяции выбирается исходя из опыта разработчика, как правило, с помощью экспериментов [De Jong, 1975, Igel et al., 2003]. Также возможен выбор размера популяции с учетом характеристик реализованного генетического алгоритма и решаемой задачи [Goldberg et al., 1992, Cvetkovic et al., 1994, Deb et al., 1999]. При этом может учитываться неопределенность приспособленности строительных блоков [Goldberg et al., 1992].
В [Eiben et al., 2004] представлены результаты сравнения различных вариантов ГА с динамическим изменением
размера
популяции. Проводится сравнение с результатами ГА с ручной настройкой
параметров и с результатами
Беспараметрического ГА (Parameter-less GA, [Harik et al., 1999]). По результатам экспериментов сделано
предположение
об эффективности алгоритмов, использующих концепцию взрослеющих
особей.
В результате анализа литературы можно выделить следующую идею: Если приспособленность в популяции улучшается,
то
популяцию следует увеличивать
. Это выражается в увеличении длительности жизни у более приспособленных
особей [Arabas
et al., 1994, Back et al., 2000], в добавлении особей в лучшую подпопуляцию [Schlierkamp-Voosen et al., 1996], в
отдаче приоритета популяции большего размера [Harik et al., 1999], в увеличении размера популяции при увеличении
приспособленности лучшей особи [Eiben et al., 2004]. В данной статье будет показано, что при увеличении значения
приспособленности целесообразно уменьшать размер популяции, а при уменьшении значения приспособленности
необходимо
увеличивать размер популяции для достижения лучшего результата.
1. Описание экспериментов и результаты
Поставлена следующая цель исследования: выяснить, как влияет изменение размера популяции на характер эволюции. Для этого проводятся запуски различных вариантов ГА, в которых количество особей в популяции изменяется в соответствии с одной из следующих стратегий:
- популяция увеличивается на 1 особь в каждом поколении –
+1
стратегия. Рассматривается два варианта запуска: с начальным размером популяции в 10 и 100 особей, обозначенные соответственноn=10 (+1)
иn=100 (+1)
; - популяция уменьшается на 1 особь в каждом поколении –
−1
стратегия. В этом случае ГА также работает с двумя различными начальными размерами популяции в 100 и 200 особей. Запуски обозначаются какn=100 (−1)
иn=200 (−1)
соответственно.
Отметим, что в проводимых экспериментах популяция не может быть меньше 10 и больше 200 особей. Размер популяции
изменяется на 1 особь, т.к. в случае сильных вариаций размера популяции возможно дополнительное влияние резкого
увеличения, либо уменьшения разнообразия хромосом в популяции при соответственно росте, либо сокращении числа
особей
в популяции. Таким образом, в запусках ГА со стратегиями n=10 (+1)
и n=100 (+1)
популяция достигала максимального
размера в 190-м и 100-м поколениях соответственно, а со стратегиями n=100 (−1)
и n=200
(−1)
размер популяции
становился равным 10 особям соответственно через 90 и 190 поколений после начала запуска.
Функции, выбранные для проведения экспериментов, представлены в табл. 1. Значения функции G> для обманчивой (deceptive) функции взяты из статьи [Whitley, 1991].
| Название | Формула |
| OneMax | |
| Сферическая функция | |
| Функция Растригина | |
| Функция Розенброка | |
| Функция Швефеля | |
| Обманчивая функция 4-го порядка |
Таблица 1
Время эволюции составляло 500 поколений. Для оценки полученных результатов проведено сравнение с ГА с фиксированным
размером популяции в 10, 100 и 200 особей (обозначенные как n=10
, n=100
и n=200
соответственно).
Для более тщательного анализа будем рассматривать операторы кроссовера со слабым и сильным смешиванием,
соответственно 1-точечный и однородный кроссовер. Также будем использовать две различные по своим параметрам
стратегии селекции: рулеточная и селекция усечением с порогом
50%, которые характеризуются соответственно слабым и
сильным давлением селекции [Blickle et al., 1995]. Вместо приспособленности особи будем использовать понятие ошибки
(error) особи, которую можно рассматривать как эквивалент расстояния от точки в поисковом пространстве,
представленной данной особью, до глобального экстремума и удобно использовать в случае минимизации целевой функции. В
качестве результатов экспериментов будем рассматривать усредненное по 50 запускам изменение средней ошибки особей в
популяции в зависимости от времени. Вероятность кроссовера для всех запусков ГА равнялась 0,8, вероятность мутации –
1/L, где L – длина хромосомы в битах. Таким образом, каждая особь в течение одного поколения мутирует в среднем 1
раз.
Наиболее характерные графики изменения средней ошибки в популяции представлены на рис.1 и 2. На рисунках по вертикальной оси откладывается значение средней ошибки, а по горизонтальной оси – номер поколения.

Рисунок 1 – Средняя ошибка особей в популяции для минимизации OneMax функции для ГА с однородным кроссовером и рулеточным отбором
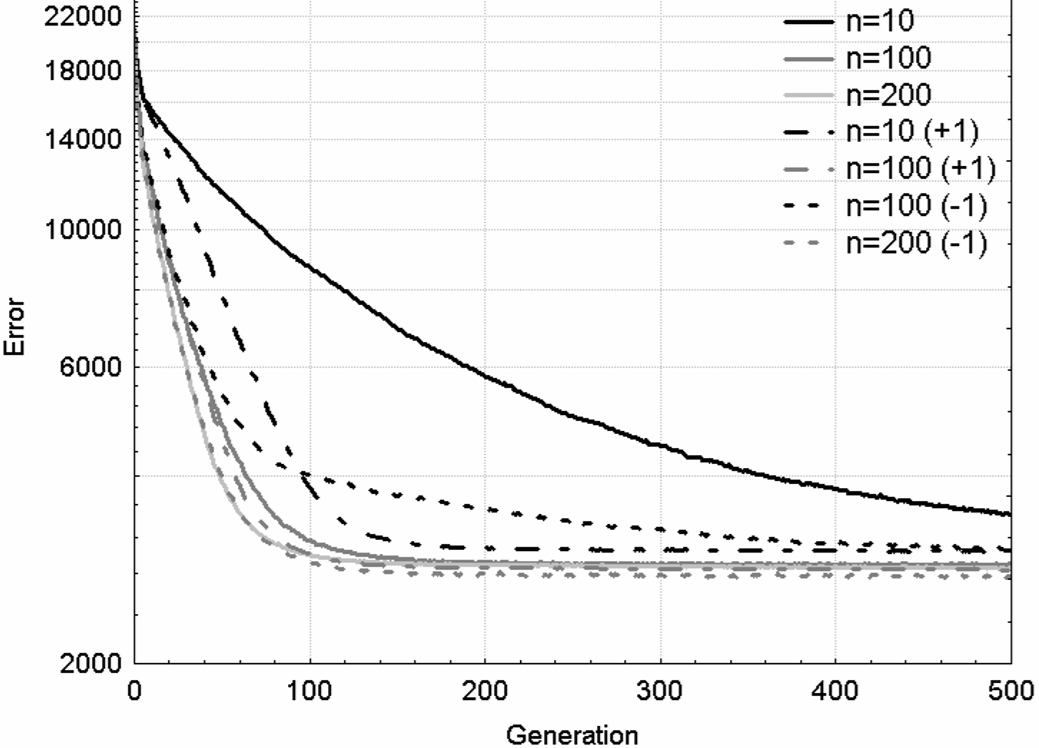
Рисунок 2 – Средняя ошибка особей в популяции для минимизации функции Швефеля для ГА с 1-точечным кроссовером и отбором усечением
Обобщим полученные результаты. Больший начальный размер популяции придает эволюционному процессу большее
ускорение
, которое можно использовать, сокращая размер популяции и, тем самым, уменьшая вычислительную сложность,
объем требуемой памяти и время работы ГА. В то же время использование обратной стратегии также способно дать хорошие
результаты, т.к. средняя ошибка достаточно быстро уменьшается благодаря увеличению популяции. Однако при этом, в
случае длительной эволюции, существенно увеличивается количество вычислений целевой функции. Данные наблюдения верны
для ГА с прямым бинарным кодированием и различными, по характеристикам, стратегиями селекции и операторами
кроссовера. Динамика средней ошибки для рассмотренных стратегий изменения размера популяции в случаях для 1-точечного
и для однородного кроссовера практически не отличаются. При замене рулеточной стратегии селекции на отбор усечением
скорость сходимости ГА значительно увеличилась, но обнаруженные закономерности для +1
и −1
> стратегий сохраняются.
Заключение
В данной работе исследовалась динамика средней ошибки в популяции при увеличении или уменьшении числа особей в популяции. Были проанализированы результаты запусков ГА с различными по характеристикам параметрами для решения 6 задач численной оптимизации. Разнообразие рассматриваемых тестовых задач и использование различных вариантов ГА позволяет надеяться на объективность полученных результатов. В результате анализа экспериментальных данных сделаны следующие выводы:
- большой начальный размер популяции оказывает сильное влияние на характер эволюции на начальном этапе. Сокращение
количества особей в популяции оказывает, в целом, незначительное влияние на скорость уменьшения средней ошибки. Тем
не менее, если популяция становится слишком малой возможно либо увеличение средней ошибки, либо прекращение эволюции,
выраженное в отсутствии улучшения, и
стабилизация
с сопутствующим дрейфом средней ошибки (рис. 1); - постепенное увеличение размера популяции, начиная с малого значения, позволяет достигать результатов, полученных для запусков с большим размером популяции, в большинстве случаев, не требуя значительного количества оценок особей. Однако в отдельных случаях для этого может понадобиться значительное число поколений.
На основании результатов экспериментов и сделанных выводов, предложим разновидность +/-
стратегии изменения
размера популяции. В предлагаемой стратегии размер популяции следует увеличить, если приспособленность лучшей особи в
популяции уменьшается, либо не изменяется, т.е. отсутствует прогресс. В случае, если приспособленность лучшей особи
увеличивается, другими словами, наблюдается эволюционное улучшение, то размер популяции следует уменьшить. Величина
изменения размера популяции не оговаривается, равно как и начальный размер популяции. При этом необходимо отметить
важность настройки других параметров генетического алгоритма, таких как стратегия селекции, операторы скрещивания и
мутации, и их характеристики.
Список использованной литературы
- [Arabas et al., 1994] Arabas J., Michalewicz Z., Mulawka J. GAVAPS—a genetic algorithm with varying population size. // Proceedings of the First IEEE International Conference on Evolutionary Computation. – IEEE Press, New York, 1994 – P.73–78.
- [Back et al., 2000] Back T., Eiben A.E., van der Vaart N.A.L. An empirical study on GAs
without parameters
// Proceedings of the 6th Conference on Parallel Problem Solving from Nature. – Springer, Berlin, 2000. – No.1917 in Lecture Notes in Computer Science – P.315-324. - [Blickle et al., 1995] Blickle T., Thiele L. A Comparison of Selection Schemes used in Genetic Algorithms (2nd Edition). TIK-Report No.11. – Swiss Federal Institute of Technology (ETH) Zurich, Switzerland, 1995.
- [Cvetkovic et al., 1994] Cvetkovic D., Muhlenbein H. The optimal population size for uniform crossover and truncation selection. – German National Research Center for Computer Science (GMD), Germany, 1994.
- [De Jong, 1975] De Jong K. An analysis of the behavior of a class of genetic adaptive systems. – PhD thesis, The University of Michigan Press, 1975.
- [Deb et al., 1999] Deb K., Agrawal S. Understanding Interactions Among Genetic Algorithm Parameters. // Foundations of Genetic Algorithms V. – Morgan Kaufmann, 1999
- [Eiben et al., 2004] Eiben A.E., Marchiori E., Valko V.A. Evolutionary Algorithms with on-the-fly Population Size Adjustment. // Parallel Problem Solving from Nature, PPSN VIII, Vol.3242 of LNCS. – Springer, 2004. – P.41-50.
- [Goldberg et al., 1992] Goldberg D.E., Deb K., Clark J.H. Genetic algorithms, noise, and the sizing of populations. // Complex Systems. – 1992. – No.6 – P.333-362.
- [Harik et al., 1997] Harik G., Cantu-Paz E., Goldberg D.E., Miller B.L. The gambler's ruin problem, genetic algorithms, and the sizing of populations. // Proceedings of the 4th IEEE Conference on Evolutionary Computation. – IEEE Press, 1997. – P.7-12.
- [Harik et al., 1999] Harik G.R., Lobo F.G. A parameter-less genetic algorithm. // Proceedings of the Genetic and Evolutionary Computation Conference, Vol.1. – Orlando, Florida, USA, 1999. – Morgan Kaufmann. – P.258-265.
- [Holland, 1975] Holland J.H. Adaptation in Natural and Artificial Systems. – The University of Michigan Press, 1975.
- [Igel et al., 2003] Igel C., Kreutz M. Operator adaptation in evolutionary computation and its application to structure optimization of neural networks. // Neurocomputing. – 2003. – No.55(1-2) – P.347-361.
- [Schlierkamp-Voosen et al., 1996] Schlierkamp-Voosen D., Muhlenbein H. Adaption of population sizes by competing subpopulations. // Proceedings of the 1996 IEEE Conference on Evolutionary Computation. – Piscataway, NY, 1996. – IEEE Press. – P.330335.
- [Whitley, 1991] Whitley D.L. Fundamental principles of deception in genetic search. // Foundations of genetic algorithms. – San Mateo, CA: Morgan Kaufmann, 1991. – P.221241.