Аннотация
Сторожук Н.О., Коломойцева И.А. - Анализ методов определения текстовой близости документов В работе представлен обзор основных алгоритмов вычисления меры сходства документов, используемых в поисковых системах и анализаторах текстов. Приведен пример расчетов близости тестовых документов, на основе полученных данных сделаны выводы о возможности использования одного из методов в системе, определяющей жанр исследуемого текста.
Общая постановка проблемы
Поиск семантического сходства между текстами является серьёзной проблемой для автоматической обработки текста. Необходимость поиска расстояния между документами возникает в различных задачах, таких как обнаружение плагиата, определение авторства документа, поиск информации, машинный перевод, формирование тестов и задач, автоматическое построение рефератов и пр. Поиску семантической схожести текстов было уделено внимание в рамках многих международных и российских конференций такими авторами как Красников И.А., Керимова С.У., Ермоленко Т.В., Бермудес С.Х.Г. [1-3].
Целью данной работы является рассмотрение наиболее используемых методов определения схожести документов, использование некоторых из них на практике и анализ результатов, полученных опытным путём, выбор самого оптимального метода для магистерской диссертации.
Введение
Автоматическая обработка текста – это преобразование текста на искусственном или естественном языке с помощью компьютера [4]. В настоящее время элементы обработки текста применяются повсеместно: переводчики, текстовые редакторы, программы для антиплагиата и автореферирования, анализаторы новостей, оптимизаторы программного кода и т.д. Следовательно, задачи эффективной автоматизированной обработки текстов остаются актуальными, стабильное увеличение объёма информации требует постоянного совершенствования алгоритмов и подходов.
Для определения жанровой принадлежности текста в планируемой программной системе следует реализовать анализатор близости загружаемого документа к документам, жанровая принадлежность которых уже определена. С этой целью могут быть использованы следующие методы:
- метод шинглов;
- скалярное произведение векторов;
- евклидово расстояние;
- манхэттенское расстояние;
- метод косинусной меры сходства;
- латентно – семантический анализ, основанный на разложении матрицы по методу сингулярного разложения (SVD - singular value decomposition).
В данной работе будут рассмотрены алгоритмы работы этих методов, их достоинства и недостатки. Кроме того, будет произведено сравнение методов, основанных на векторном представлении документов, с точки зрения эффективности их работы и рациональности их использования в магистерской работе для определения жанровой принадлежности документа.
Метод шинглов
В процессе изучения вопроса был рассмотрен алгоритм шинглов как метод лексического анализа текстов на предмет их схожести, полного или частичного совпадения. В основе этого метода лежит разбиение текстов на группы слов одинаковой длины и последующее сравнение их хешей. Этапы, которые проходит тексты, подлежащие сравнению:
- приведение текста к единой нормальной форме;
- разбиение на шинглы заданной длины;
- вычисление хешей шинглов;
- случайный выбор 84 значений контрольных сумм;
- сравнение сумм, определение результата [5].
Приведение текста к единой нормальной форме или канонизация текстов подразумевает удаление из исходного текста предлогов, союзов, знаков препинания, тегов и прочих незначительных элементов, которые не должны участвовать в сравнении. Кроме того, на этом шаге оставшиеся слова приводятся к именительному падежу, единственному числу, отбрасываются окончания и суффиксы. Для этих целей используют алгоритмы стемминга или лемматизации, рассмотренные в статье [6] и используемые независимо от метода дальнейшего анализа полученных терминов.
Шинглы – выделенные из статьи последовательности слов. Из сравниваемых текстов необходимо выделить определенное число слов (обычно используют 10 слов), идущих друг за другом. Выборка происходит внахлест, таким образом в результате получается набор шинглов для каждого исследуемого документа.
Принцип алгоритма шинглов заключается в сравнении случайной выборки контрольных сумм шинглов (подпоследовательностей) двух текстов между собой. Так как число шинглов каждого документа приближается к числу слов этого документа, основной проблемой использования алгоритма является низкая скорость. Увеличение исходных текстов характеризуется экспоненциальным ростом операций сравнения, что критически отразится на производительности [7].
В рамках исследования анализа расстояния между текстами, выделения общей темы документов и определения их близости метод шинглов не является подходящим, так как требует практически полного совпадения терминов и их последовательностей. Использование этого алгоритма широко практикуется для поиска копий и дубликатов текста, выявления плагиата, поиска документов, соответствующих жестко заданному запросу.
Методы, основанные на векторной модели представления документов
Другой подход к анализу текстов предполагает выявление схожести на основании пропорций вхождения слов в каждый из документов. Для подготовки данных для использования этого подхода используется канонизация текста, описанная выше и подход под названием «мешок слов». Его суть состоит в том, что для дальнейшего анализа важно число вхождения конкретных слов, а не морфологически формы слов и их порядок в документе.
Предположим, что каждую тему можно охарактеризовать определенным набором слов и частотой их появления. Если в тексте конкретный набор слов употребляется с определенными частотами, то текст принадлежит к определенной теме. На основании этой информации строится таблица «слово-документ», где строки соответствуют терминам, полученным после канонизации, а столбцы – исследуемым документам. В каждой ячейке может храниться булево значение, которое показывает наличие хотя бы одного вхождения термина в документ, частота слова в документе или вес термина. Такой способ представления текстов в виде таблицы (или матрицы) называется векторной моделью текста [8]. Теперь, для того чтобы сравнить два документа, нужно определить меру схожести двух столбцов таблицы.
Для анализа методов были выбраны исходные данные, представленные ниже (рис. 1). Здесь q – эталонный документ (запрос), а d1, d2, d3 – документы, которые надо проанализировать на схожесть с q. Размеры документов практически одинаковы, таким образом предварительную нормировку длины производить не требуется.

Первым шагом после лемматизации тестовых документов является формирование единого списка терминов из трех документов, их сортировка и удаление повторяющихся. Далее произведем подсчет подсчёт числа документов, в которые входит термин (tf). В таблице 1 приведен фрагмент списка терминов с соответствующими значениями.
Таблица 1 - Показатели числа документов ( tf)
Термины |
Tf d1 |
Tf d2 |
Tf d3 |
Число документов |
балок |
0 |
1 |
0 |
1 |
более |
0 |
1 |
0 |
1 |
болот |
0 |
0 |
1 |
1 |
… |
… |
… |
… |
… |
они |
0 |
1 |
0 |
1 |
основн |
0 |
0 |
1 |
1 |
откры |
1 |
0 |
0 |
1 |
относят |
0 |
0 |
1 |
1 |
песк |
1 |
0 |
0 |
1 |
песч |
1 |
1 |
1 |
3 |
пород |
0 |
1 |
0 |
1 |
… |
… |
… |
… |
… |
На следующем этапе рассчитываются показатели idf – обратная документальная частота - функция от величины, обратной количеству документов коллекции, в которых встречается этот термин (1). Следует отметить, что основание логарифма может быть любым, для простоты чаще всего используют 2 или 10 [9].

где n – общее число рассматриваемых документов (в данном примере n=3);
df – частота в коллекции или число документов, в которые входит этот термин.
Скомбинируем частоту термина в документе tf и обратную документную частоту idf, чтобы получить вес каждого термина в каждом документе. Схема взвешивания tf-idf присваивает каждому термину t его вес в документе d на основе формулы 2.

Использование такого показателя позволяет усилить отличие термина, если он встречается часто в небольшом количестве документов и уменьшить значение термина и релевантность документа, если термин встречается во многих документах или используется всего несколько раз.
Каждый документ можно интерпретировать как вектор, состоящий из компонент, соответствующих каждому термину в словаре и весов каждого компонента, представленных в виде tf-idf. Таким образом, в таблице 2 представлены векторы для исследуемых документов.
Таблица 2 – Векторы документов
Термины |
idf |
tf-idf d1 |
tf-idf d2 |
tf-idf d3 |
балок |
1,585 |
0 |
1,585 |
0 |
более |
1,585 |
0 |
1,585 |
0 |
болот |
1,585 |
0 |
0 |
1,585 |
… |
… |
… |
… |
… |
они |
1,585 |
0 |
1,585 |
0 |
основн |
1,585 |
0 |
0 |
1,585 |
откры |
1,585 |
1,585 |
0 |
0 |
относят |
1,585 |
0 |
0 |
1,585 |
песк |
1,585 |
1,585 |
0 |
0 |
песч |
0 |
0 |
0 |
0 |
пород |
1,585 |
0 |
1,585 |
0 |
… |
… |
… |
… |
… |
Заданный поисковый запрос следует также привести к векторному представлению. Для этого аналогичным образом были вычислены показатели tf, tf-idf, представленные в таблице 3.
Таблица 3 – Показатели tf, tf-idf для запроса
Термины |
tf |
tf/max(tf) |
Число документов |
tf-idf |
гранит |
1 |
0,5 |
1 |
0,792 |
и |
1 |
0,5 |
1 |
0,292 |
известняк |
1 |
0,5 |
1 |
0,292 |
карбонатн |
1 |
0,5 |
0 |
0 |
мелов |
1 |
0,5 |
1 |
0,792 |
мергел |
1 |
0,5 |
1 |
0,792 |
на |
2 |
1 |
1 |
0,585 |
откры |
1 |
0,5 |
1 |
0,792 |
отслоен |
2 |
1 |
0 |
0 |
песк |
1 |
0,5 |
1 |
0,792 |
произраст |
1 |
0,5 |
0 |
0 |
эродирован |
1 |
0,5 |
1 |
0,792 |
Теперь, для того чтобы сравнить два документа, нужно определить меру схожести двух столбцов таблицы. Существует множество методов, основанных на векторном представлении документов. В рамках данной работы будут рассмотрены следующие:
- скалярное произведение векторов;
- евклидово расстояние;
- манхэттенское расстояние;
- метод косинусной меры сходства.
Скалярное произведение векторов вычисляется на основании полученных показателей tf-idf по формуле 3.
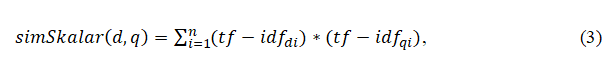
где n – число терминов;
i – переменная – счетчик.
Согласно формуле были получены следующие значения схожести для документов:
- SimSkalar (d1) = 8,734;
- SimSkalar (d2) = 0,684;
- SimSkalar (d3) = 1,256;
На основании полученных показателей близости следует отметить, что чем больше показатель скалярного произведения, тем ближе документы по смыслу. Таким образом, первый документ наиболее схож с запросом.
Евклидово расстояние трактуется как расстояние между точками или косинус угла между векторами, представляющими документы в пространстве терминов, и рассчитывается по формуле 4.

Получены следующие значения схожести для документов:
- SimEvklid (d1) = 2,069;
- SimEvklid (d2) = 2,540;
- SimEvklid (d3) = 2,228.
Следует отметить, что принцип выбора лучшего документа другой: чем ниже результат, тем ближе документы.
Манхеттенское расстояние (расстояние Хемминга, расстояние городских кварталов) вычисляется как сумма абсолютных значений координатных расстояний векторов, представляющих документы в пространстве терминов [10], и рассчитывается по формуле 5:
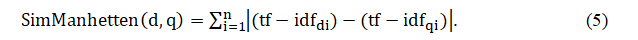
Получены следующие расстояния между документами и запросом:
- SimManhetten (d1) = 5,925;
- SimManhetten (d2) = 6,925;
- SimManhetten (d3) = 6,510.
В большинстве случаев эта мера расстояний приводит к таким же результатам анализа, как и простое евклидово расстояние, что можно наблюдать по полученным результатам.
Вычисление разности между векторами способами, приведенными выше, приводит к следующему недостатку: такая разность между двумя схожими документами может быть значительной, если один из документов значительно длиннее другого. Таким образом, относительное распределение в документах может быть одинаковым, но абсолютные частоты терминов будут намного больше. Для того чтобы компенсировать влияние длины документа, используем метод косинусной меры сходства (формула 6).

В результате получим:
- SimCos (d1) = 0,822;
- SimCos (d2) = 0,054;
- SimCos (d3) = 0,093.
Косинусное сходство двух документов изменяется в диапазоне от 0 до 1, поскольку частота термина tf-idf не может быть отрицательной. Угол между двумя векторами частоты термина не может быть больше, чем 90°. [11]
Cведем в общую таблицу полученные результаты.
Таблица 4 – Результаты вычислений схожести документов с запросом
Документ/метод |
Эвклидово расстояние |
Манхеттенское расстояние |
Скалярная мера сходства |
Косинусная мера сходства |
d1 |
2,069 |
5,925 |
8,734 |
0,822 |
d2 |
2,540 |
6,925 |
0,684 |
0,054 |
d3 |
2,228 |
6,510 |
1,256 |
0,093 |
Согласно полученным значениям схожести, конечный порядок, в котором документы будут представлены как результат запроса, будет: d1, d3, d2. Анализируя эти показатели, следует обратить внимание, что значения схожести по эвклидовому и манхеттенскому методам на самом деле – расстояния между векторами. Таким образом, чем расстояние меньше, тем более документ схож с запросом. Методы, использующие скалярное произведение и косинусные показатели, в результате возвращают именно сходство, то есть наилучший документ тот, который имеет наибольший показатель сходства.
Без использования специальных методов анализа результаты можно назвать корректными. Первый документ описывает то же самое явление, что и запрос, однако информация взята из другого источника. Второй и третий документы значительно разнятся от запроса с точки зрения их содержания и показатели косинусного сходства наиболее выразительно это иллюстрируют: значение сходства для первого документа более чем в 9 раз превышает показатель сходства для второго документа. Одна из причин популярности косинусного сходства состоит в том, что оно эффективно в качестве оценочной меры, особенно для разреженных векторов, так как необходимо учитывать только ненулевые измерения [9]. Анализируя результаты манхеттенского расстояния и эвклидового расстояния, можно предположить, что документы практически равноценны по сходству, хотя на самом деле это не так. Другим недостатком этих методов является полный перебор векторов и вычисление расстояний даже для нулевых точек, что несет за собой увеличение требований к производительности.
На основании проделанных расчетов и анализа описанных методов, основанных на векторной модели, лучшим методом для определения близости документов был определен метод косинусного сходства.
Метод латентно-семантического анализа
Метод латентно – семантического анализа (LSA -Latent semantic analysis) применяется для рекомендательных систем, информационного семантического поиска, разделения текстов по тематикам без обучения, SEO анализа текста.
Данный метод предполагает более глубокий анализ терминов: вместо таблицы "слово-документ" как в предыдущем методе формируются таблицы "слово-тема" и "тема-документ". Это требуется для того, чтобы минимизировать недостатки предыдущих алгоритмов:
- зашумленности (цитаты, другие вставки текста на другом языке не должны влиять на тематику);
- размерности (вычисление расстояние между векторами становится медленной процедурой при больших объемах данных);
- разреженности (большинство ячеек в таблице tf будут нулевыми).
Метод латентно – семантического анализа включает в себя следующие этапы:
- разбиение документа на слова, удаление знаков препинания и стоп-слов;
- стемминг или лемматизация;
- исключение терминов, встречающихся в единственном экземпляре;
- построение матрицы слово-документ (бинарные значения, tf или tf-idf);
- разложение матрицы методом SVD (A = U * V * WT);
- выделение строк матрицы U и столбцов W, которые соответствуют наибольшим сингуляр¬ным числам (их может быть от 2-х до минимума из числа терминов и документов).
Конкретное количество учитываемых собственных чисел определяется предполагаемым количеством семантических тем в задаче. Чем больше сингулярное число, тем сильнее в коллекции проявлена тема. Выделение трех таблиц из одной позволяет снизить размерность данных - не нужно хранить всю матрицу слово-документ, достаточно только сравнительно небольшого набора числовых значений для описания каждого слова и документа [12].
Ограничениями LSA являются:
- значительная вычислительная сложность метода;
- для более эффективного и рационального использования алгоритмов следует брать большие выборки исходных данных;
- недостатком является допущение, что карта слов в документах не имеет вид нормального распределения, для устранения требуется дорабатывать алгоритм.
Выводы
В статье представлен обзор наиболее распространенных методов, применяемых для определения близости документов и последующего анализа результатов. Для разработки собственной системы будет использован метод косинусного сходства как наиболее быстрый и показательный.
Список использованной литературы
- Agirre, E. Semantic textual similarity [Текст] / E. Agirre, D. Cer, M. Diab, A. Gonzalez-Agirre, G. Weiwei // 2nd Joint Conference on Lexical and Computational Semantics. – Атланта: 2013. – С. 32-43.
- Красников, И.А. Гибридный алгоритм классификации текстовых документов на основе анализа внутренней связности текста [Текст] / И. А. Красников, Н. Н. Никуличев [Электронный ресурс] // Интернет-ресурс «Инженерный вестник Дона». – Режим доступа: ivdon.ru/ru/magazine/archive/n3y2013/1773
- Харламов, А. А. Сравнительный анализ организации систем синтаксических парсеров [Текст] / А. А. Харламов, Т. В. Ермоленко, Г. В. Дорохина [Электронный ресурс] // Интернет-ресурс «Инженерный вестник Дона». – Режим доступа: ivdon.ru/ru/magazine/archive/n4y2013/2015
- Автоматическая обработка текста [Электронный ресурс] / Интернет-ресурс. – Режим доступа: http://russkiyyazik.ru/9/
- Афанасьев, А. Ю Использование алгоритма шинглов для анализа ответов на вопросы открытого типа в системе контроля знаний [Текст] / А. Ю. Афанасьев, В. М. Глушань // Сб. науч. Тр. 5й Всероссийской научно-технической конференции аспирантов, студентов и молодых ученых. – Ульяновск: 2008. – С. 44-50.
- Сторожук, Н. О., Коломойцева И.А. Анализ алгоритмов лексической и морфологической обработки текстов c целью определения жанровой принадлежности / Н. О. Сторожук, И. А. Коломойцева // Материалы V Международной научно-технической конференции «Современные информационные технологии в образовании и научных исследованиях» (СИТОНИ-2017). – Донецк: ДонНТУ, 2017. – С. 191-195.
- Агеева, С. П. Система поиска сходства шаблонизированных строк [Электронный ресурс] / Интернет-ресурс. – Режим доступа: https://moluch.ru/archive/81/14569/
- Векторная модель [Электронный ресурс] / Интернет-ресурс. – Режим доступа: http://www.machinelearning.ru/wiki/index.php?title=Векторная_модель
- Маннинг, К.Д. Введение в информационный поиск / К. Д. Маннинг, П. Рагхаван, Х. Шютце – М: ООО «И.Д. Вильямс», 2011. – 528 с.
- Расстояние_Хэмминга [Электронный ресурс] / Интернет-ресурс. – Режим доступа: https://neerc.ifmo.ru/wiki/index.php?title=Расстояние_Хэмминга
- Компьютерный анализ текста [Электронный ресурс] / Интернет-ресурс. – Режим доступа: http://lab314.brsu.by/kmp-lite/CL/CL-Lect/KAT.htm
- Алгоритм LSA для поиска похожих документов [Электронный ресурс] / Интернет-ресурс. – Режим доступа: https://netpeak.net/ru/blog/algoritm-lsa-dlya-poiska-pohozhih-dokumentov/