УДК 330.4:004.032.26 https://doi.org/10.24158/pep.2018.5.12

Видмант Олег Сергеевич

аспирант Финансового университета при Правительстве Российской Федерации

ПРОГНОЗИРОВАНИЕ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ С ИСПОЛЬЗОВАНИЕМ РЕКУРРЕНТНЫХ НЕЙРОННЫХ СЕТЕЙ LSTM

Vidmant Oleg Sergeevich

PhD student, Financial University under the Government of the Russian Federation

FORECASTING FINANCIAL TIME SERIES WITH LSTM RECURRENT NEURAL NETWORKS

Аннотация:

В работе исследуется возможность прогнозирования цен закрытия волатильного финансового инструмента (Close ) с использованием специальной архитектуры рекуррентных нейронных сетей (Long Short Term Memory , LSTM ). Набором данных для исследования служит выборка из временного ряда фьючерса Сбербанка за 2летний промежуток времени и с 5минутными интервалами между наблюдениями. На основе выбранного временного ряда формируются последовательности с фиксированным окном смещения; кроме того, используемые данные нормализуются на отрезке[0 : 1]. По отношению к сформированным данным применяются нейросетевые модели, состоящие из двух слоев рекуррентных, а также двух агрегирующих слоев прямого распространения. По окончании процесса обучения моделиLSTM производится сравнение прогнозированных данных и исторических цен закрытия. В результате сравнения продемонстрировано, что модель рекуррентных нейронных сетей на основе архитектуры LSTM способна прогнозировать поведение инструмента на финансовом рынке.

Ключевые слова:

нейронные сети, рекуррентные сети, прогнозирование, финансовые рынки, фьючерсы.

Чуть более десяти лет назад, в середине 2000–х гг., машинное обучение получило новый виток развития, что было связано с именами двух исследователей Университета в Торонто – Джеффри Хинтона и Йошуа Бенджи, которые нашли более эффективный способ обучения. И в данный момент во многих областях лучшие результаты получаются именно с использованием глубоких нейронных сетей. Одним из прорывов было кардинальное улучшение результатов при решении задач распознавания, и сейчас многие лидеры мирового рынка используют глубокие нейросети для решения задач перевода (Microsoft [1], Google [2], IBM [3]), голосовых помощников (Siri, AmazonEcho), распознавания лиц (Facebook [4]), беспилотного вождения или даже игр (покер, го). Сети прямого распространения, или многослойные перцептроны, исследованные ранее, имеют фиксированное число входов, и каждый из них воспринимается остальными как независимый. Однако в рекуррентных сетях связи между нейронами не ограничиваются исключительно движением информации в одну сторону, но также имеется возможность вернуть значение самому себе. Таким образом, нейрон может запоминать информацию, которая была подана ранее на вход. Именно поэтому рекуррентные нейронные сети являются наилучшим выбором для прогнозирования временных рядов и последовательностей. Задачи по характеру входов и выходов разделяют на пять вариантов [5]:

• один вход, один выход (one–to–one);
• один вход, последовательность выходов (one–to–many);
• последовательность входов, один выход (many–to–one);
• последовательность на входе, последовательность на выходе (many–to–many);
• синхронизированные последовательности входов и выходов (synchronized many–to–many).

В данной статье решается регрессионная задача «many–to–one» при обучении с учителем при использовании рекуррентных слоев. Обычные рекуррентные сети очень плохо справляются с ситуациями, когда нужно что-то запомнить надолго: влияние скрытого состояния или входа с шага t на последующие состояния рекуррентной сети экспоненциально затухает. Именно поэтому в данном исследовании использована модель LSTM [6] (Long Short–Term Memory), где добавляется дополнительная ячейка для моделирования долгой памяти. Подобная задача рассматривалась в статье Prediction Stock Prices Using LSTM [7], где в качестве инструмента выступал инструмент NIFTY 50 с 5-летней временной выборкой и последующим обучением на 250 и 500 эпохах, а также в работе М. Хэнссона [8], где после анализа было сформировано заключение о том, что рекуррентные нейронные сети LSTM могут прогнозировать события не на всех рынках и инструментах. Предполагается, что на более развитых рынках происходит снижение качества результатов за счет использования аналогичных/обратных моделей для спекулятивных действий. Таким образом, целью данной статьи является проверка гипотезы о возможности прогнозирования российского финансового инструмента. Эта задача особенно актуальна в последние 5–6 лет, на протяжении которых мы могли наблюдать волатильное поведение большинства инструментов вследствие как страновых рисков, так и экономического кризиса. В качестве инструмента для прогнозирования воспользуемся фьючерсом Сбербанка (SPFB.SBRF) с двухлетней глубиной выборки, а также 5-минутными временными интервалами (см. табл. 1).

Таблица 1 – Исходные данные инструмента

Для улучшения работы нейронных сетей воспользуемся нормализацией данных в пределах [0 : 1] [9] (см. табл. 2).

Таблица 2 – Нормализация данных инструмента

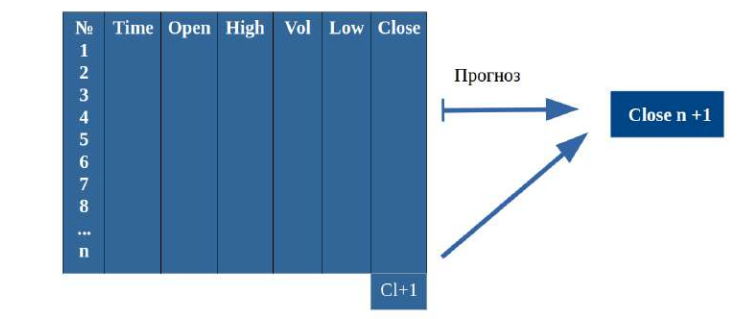
Рекуррентные нейронные сети будут принимать в качестве входных данных последовательность значений, в данном случае в качестве входных данных будет использована матрица, состоящая из 6 признаков и фиксированного скользящего окна длиной n (см. рис. 1).

Рисунок 1 – Данные для обучения модели рекуррентных слоев

Используем в качестве переменной скользящего окна значение n = 20, а также разделим выборку в соотношении 90 : 10 на тренировочные данные и данные для проверки гипотезы (отложенные данные). Также выделим 10 % от тренировочных данных на тестирование алгоритма. Таким образом получим следующее соотношение:

• данные для тренировки: 75713 x 20 x 6;
• данные для тестирования: 8413 x 20 x 6.

Конструирование нейронной сети показано на рис. 2.

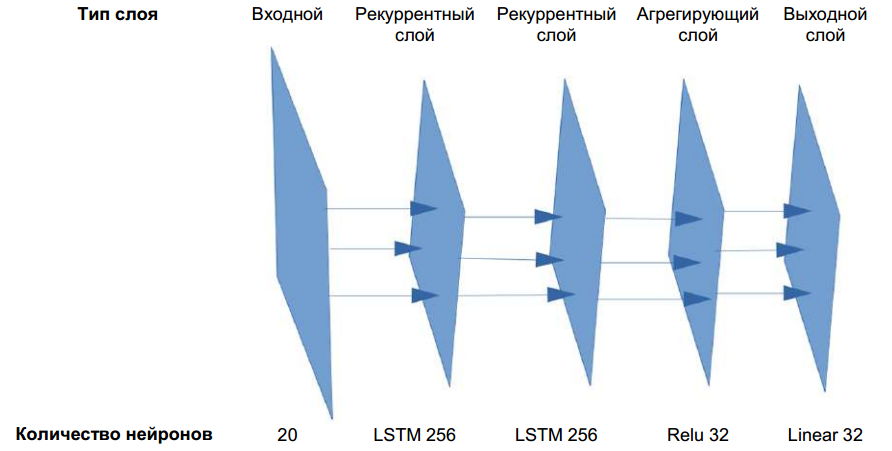
Рисунок 2 – Строение нейронной сети

На вход нейронной сети подается матрица размерностью 20 x 6, далее значения передаются на рекуррентный слой, который состоит из 256 нейронов рекуррентной нейронной сети, далее процедура повторяется и по окончании результаты агрегируются слоем прямого распространения с функцией активации Relu [10]. Конечный результат поступает на выходной слой с одним нейроном и линейной функцией активации. Для создания нейронной сети воспользуемся языком программирования Python, а также библиотеками для обработки и визуализации данных:

• pandas;
• numpy;
• matplotlib;
• keras (в качестве основы tensorflow);
• sklearn.

В качестве функции потерь в процессе обучения используется среднеквадратическая ошибка (Mean Squared Error), оптимизация осуществляется с использованием алгоритма Adam [11]. Обучение производится итеративно в течение 10 эпох для отслеживания возможного переобучения (рис. 3).

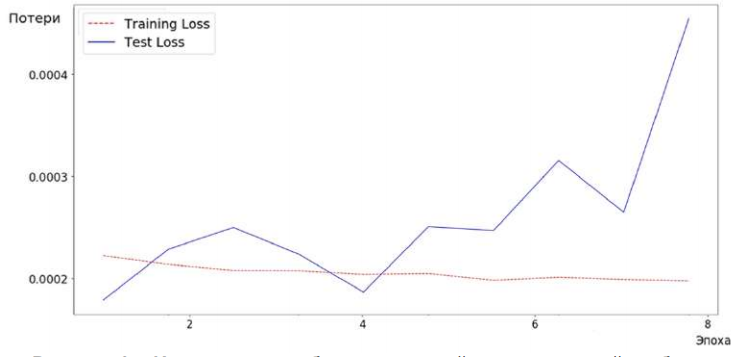
Рисунок 3 – Изменение ошибки на тестовой и проверочной выборке

Как можно заметить, потери тестовой выборки возрастают после первой эпохи, в которой наблюдается минимальное значение ошибки. Также можно заметить монотонное убывание ошибки тренировочных данных, что при сопоставлении всей полученной информации означает, что модель начинает переобучаться на основании тренировочных данных. Таким образом, для получения наилучшего результата воспользуемся моделью с первой эпохи. После обучения получаем следующие значения ошибок:

• Train Score: 0.00002 MSE;
• Test Score: 0.00036 MSE.

Визуализируем прогнозируемое нормализованное изменение цены (НИЦ) на месячном временном отрезке (отложенном на основе 5–минутных интервалов), а также сравним их динамику с нормализованными историческими движениями финансового инструмента (рис. 4).

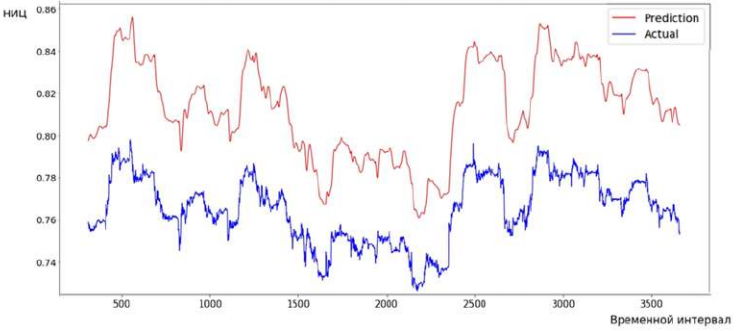
Рисунок 4 – Сравнение прогнозируемых показателей и исторических данных

При анализе рисунка 4 можно заметить, что прогностическая кривая отображает динамику поведения финансового актива. Несмотря на то что линия прогноза (верхняя кривая) является более сглаженной, она повторяет изменение цены, что в свою очередь означает: рекуррентные нейронные сети могут прогнозировать поведение рыночных активов. Уровни ошибки на тренировочной и валидационной выборке показывают, что модель несколько хуже прогнозирует реальные данные, это может быть обусловлено изменяющимися процессами в отложенных данных. В то же время усложнение модели и создание агрегирующих слоев позволяет не использовать большие мощности для оптимизации на 250 или 500 эпохах. Также можно выделить некоторые недостатки данной модели:

• во время обучения сложно трактовать результаты, это накладывает ограничения на возможность улучшения модели;
• невозможно предсказать, когда изменится динамика рынка и модель перестанет работать;
• каждому отдельному инструменту соответствует натренированная на его данных модель, использование других моделей снижает эффективность прогнозирования.

Построенная модель может быть использована как для решения задач риск–менеджмента (для регуляризации резервного капитала по отдельному инструменту), так и для выполнения краткосрочных финансовых операций.

Ссылки:

1. Semantic Object Parsing with Graph LSTM / Xiaodan Liang [et al.] // Proceedings ECCV 2016. Pt. I / ed. by B. Leibe [et al.]. Cham, 2016. P. 125–143.
2. Application of Pretrained Deep Neural Networks to Large Vocabulary Speech Recognition / N. Jaitly [et al.] // Proceedings of Interspeech. 2012.
3. Making Deep Belief Networks Effective for Large Vocabulary Continuous Speech Recognition / T.N. Sainath [et al.] // Automatic Speech Recognition and Understanding. 2011. P. 30–35.
4. DeepFace: Closing the Gap to Human–Level Performance in Face Verification / Y. Taigman et al. // Proceedings 2014 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC, 2014. P. 1701 –1708.
5. Karpathy A. The Unreasonable Effectiveness of Recurrent Neural Networks [Электронный ресурс]. 2015. URL: http://karpathy.github.io/2015/05/21/rnn-effectiveness/ (дата обращения: 27.05.2018).
6. LSTM: A Search Space Odyssey [Электронный ресурс] / K. Greff [et al.] // IEEE Transactions on Neural Networks and Learning Systems.2017. Vol. 28, no. 10. P. 2222–2232.
7. Roondiwala M., Patel H., Varma S. Predicting stock prices using LSTM / // International Journal of Science and Research. 2017. Vol. 6, no. 4. P. 1754–1756.
8. Hansson M. On stock return prediction with LSTM networks // Lund University, 2017.
9. Sklearn.preprocessing.MinMaxScaler [Электронный ресурс]. URL: http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html (дата обращения: 27.05.2018).
10. Glorot X., Bordes A., Bengio Y. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics [Электронный ресурс]. 2011. URL: http://proceedings.mlr.press/v15/glorot11 a.html (дата обращения: 27.05.2018).
11. Kingma D.P., Lei Ba J. Adam: A Method for Stochastic Optimization [Электронный ресурс]. URL: https://arxiv.org/pdf/1412.6980.pdf (дата обращения: 27.05.2018).

References:

Glorot, X, Bordes, A & Bengio, Y 2011, Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics,viewed 27 May 2018, .

Greff, K (et al.) 2017, ‘LSTM: A Search Space Odyssey’, IEEE Transactions on Neural Networks and Learning Systems,Vol. 28, no. 10, pp. 2222–2232. https://doi.org/10.1109/tnnls.2016.2582924.

Hansson, M 2017, ‘On stock return prediction with LSTM networks’, LundUniversity, n.p.

Jaitly, N (et al.) 2012, ‘Application of Pretrained Deep Neural Networks to Large Vocabulary Speech Recognition’, Proceedings of Interspeech.

Karpathy, A 2015, The Unreasonable Effectiveness of Recurrent Neural Networks,viewed 27 May 2018, .

Kingma, DP & Lei Ba J 2018, Adam: A Method for Stochastic Optimization,viewed 27 May 2018, .

Roondiwala, M, Patel, H & Varma, S 2017, ‘Predicting stock prices using LSTM’, International Journal of Science and Research,Vol. 6, no. 4, pp. 1754–1756.

Sainath, TN (et al.) 2011, ‘Making Deep Belief Networks Effective for Large Vocabulary Continuous Speech Recognition’, Automatic Speech Recognition and Understanding, pp. 30–35. https://doi.org/10.1109/asru.2011.6163900.

Sklearn.preprocessing.MinMaxScaler2018, viewed 27 May 2018, .

Taigman, Y (et al.) 2014, ‘DeepFace: Closing the Gap to Human-Level Performance in Face Verification’, Proceedings 2014 IEEE Conference on Computer Vision and Pattern Recognition,Washington, DC, pp. 1701 –1708. https://doi.org/10.1109/cvpr.2014.220.

Xiaodan Liang (et al.) & Leibe, B (et al.) (eds.) 2016, ‘Semantic Object Parsing with Graph LSTM’, Proceedings ECCV 2016, Pt. I, Cham, pp. 125–143. https://doi.org/10.1007/978-3-319-46448-0_8.