Аннотация
Скрипай В.В., Андрюхин А.И. Методы прогнозирования динамики финансовых рынков. Рассмотрены основные методы прогнозирования динамики финансовых временных рядов. Проведен сравнительный анализ двух способов выявления функции зависимости во временных рядах.
Главной проблемой при прогнозировании и анализе финансовых временных рядов является построение моделей, которые наиболее точно отражают их динамику. Возникновение тех или иных внешних факторов, как правило, не отражается в предыстории финансовых временных рядов, но вызывает нарушение их динамики. Именно в этом заключается особенность практически всех финансовых временных рядов. Сложностью моделирования изменений финансовых рынков является их нелинейность, что не позволяет эффективно применять такие инерционные методы, как ARIMA, MACD. Нелинейность финансовых систем проявляется в эффекте бабочки
, когда очень маленькие изменения параметров влекут за собой большие последствия. Одной из задач современной науки является разработка моделей и методов для точного прогнозирования таких процессов.
В настоящее время популярными и востребованными являются методы, основанные на вейвлет–преобразовании [1]и методы прогнозирования временных рядов, основанные на технологии нейронных сетей [2].
В последнее время для решения выше поставленной задачи появилось и развивается такое направление, как эконофизика, основой которой является исследование экономических явлений, объектов и систем методами физики [3]. Последняя породила методы анализа частотных характеристик временного ряда [4, 5]. Наиболее распространенным методом изучения временных рядов является классическая сезонная декомпозиция. Она базируется на возможности представления данных временного ряда в виде двух моделей – аддитивной и мультипликативной. В этих моделях выделяются три компонента:
- тренд;
- периодическая или циклическая компонента;
- случайная компонента.
Тренд отражает долгосрочные изменения, которые наблюдаются во временном ряду, когда циклическая и нерегулярная компоненты исключены. Обычно предполагается, что тренд можно представить линейной зависимостью, т.е. визуально в виде прямой линии.
Цикличность отражает колебания во временном ряду, вызванные определенными факторами. Циклический фактор, как правило, повторяется через определенный период, хотя точная картина показателей ряда может меняться.
ПК МВТУ
реализует следующие режимы работы: моделирование, оптимизация, анализ, синтез ,контроль и управление.
Случайная компонента – это то влияние, которое может наблюдаться после завершения исключения влияния тренда и цикличного факторов.
Прежде чем прогнозировать котировки с помощью методов, основанных на частотном разложении временного ряда, был проведен анализ временного ряда с помощью классических методов прогнозирования. В качестве учебной выборки были взяты данные котировок Forex за октябрь 2011 года с периодичностью в сутки, 4 часа, 1 час, 30 минут.
Чтобы описать зависимость ряда была предложена классическая регрессионная модель, учитывающая две основные компоненты временного ряда – тренд и циклическую компоненту. Она имеет вид:
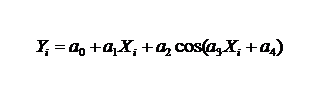
Также было выдвинуто предположение о том, что качество прогноза будет зависеть от размера окна – количества данных, на основе которых будет построена зависимость, и смещения (сдвига) этого окна относительно первого элемента. Прогноз рассчитывался на один последующий день. Качество прогноза оценивалось аддитивной ошибкой с помощью метода наименьших квадратов. Расчеты были проведены в программном пакете Maple 15.
Предложено два варианта расчета модели:
1–й метод – программа учитывала полную зависимость и вычисляла сразу все параметры модели;
2–й метод – на первом этапе программа выявляла тренд (т.е. вычисляла первые два параметра), затем из исходных данных вычитала значение смоделированного тренда, и по остатку находила циклическую зависимость (т.е. вычисляла остальные параметры).
Для вывода полученных расчетов в графическом виде были использованы следующие показатели:
р1 – отношение фактического значения временного ряда к спрогнозированному;
m – размер временного окна;
sdv – сдвиг временного окна относительно первого элемента.
Результаты вычислений по первому методу приведены на рисунке 1.
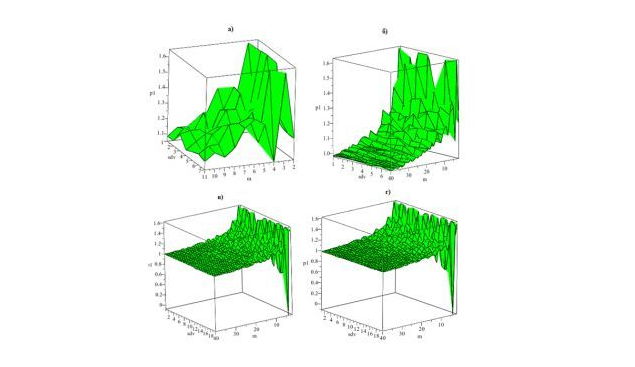
Рис. 1. Зависимость качества прогноза от размера временного окна и его расположения (1–й метод) с периодичностью данных: а) 24 часа; б) 4 часа; в) 1час; г) 30 минут.
Из данных, представленных на рисунке 1, можно увидеть, что с увеличением размера временного окна точность прогноза увеличивается. Для часовой и получасовой периодичности минимальное значение оптимального размера окна равно 20 периодам, т.е. отклонения прогнозных значений от фактических составляют не более 3 %, а также сглаживается влияние сдвига на качество прогноза.
Также были рассчитаны средние значения параметра р1 для размера окна по первому методу расчета. Поскольку для всех четырех периодичностей графики имеют примерно одинаковую характерно изогнутую кривую, в работе представлен график для периодичности в 4 часа.
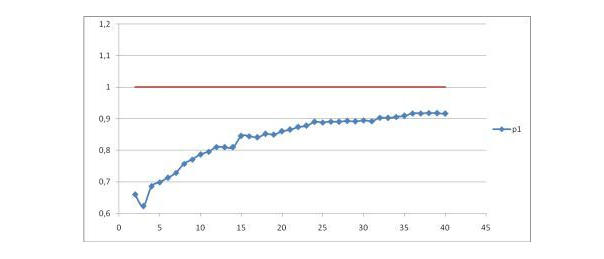
Рис. 2. Зависимость качества прогноза от размера временного окна (1–й метод)
Анализ рисунка 2 подтверждает, что точность прогноза по данному методу вычисления повышается с увеличением размера временного окна.
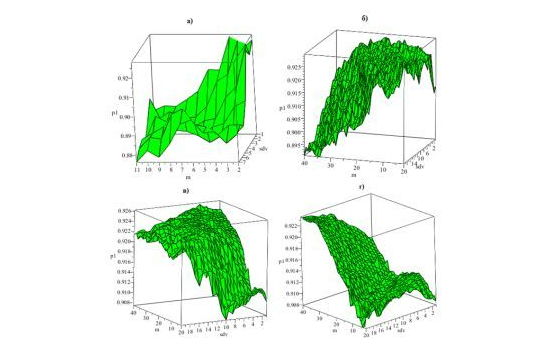
Рис. 3. Зависимость качества прогноза от размера временного окна и его расположения (2–й метод) с периодичностью данных: а) 24 часа; б) 4 часа; в) 1час; г) 30 минут.
Результаты вычислений по второму методу приведены на рис.3. Из данных, представленных на рис.3, можно увидеть, что при расчете зависимостей данным методом не существует общей характерной зависимости качества прогноза от размера временного окна или его смещения по временному ряду, .как в предыдущем случае.
Сравнивая эти два метода можно увидеть, что при первом методе прогнозирования разброс от наилучшей до наихудшей точности прогноза составил в среднем 60 %, а при втором – не превысил 10 %. Однако, с увеличением размера временного окна в первом методе была достигнута точность прогноза в 95-97%, а при прогнозировании вторым методом она колебалась в диапазоне 87-93%. Следовательно, можно сделать вывод, что второй классический метод декомпозиция является более надежным для прогнозирования с точностью прогноза 90%.
Необходимо подчеркнуть, что эти результаты носят локальный характер для рассматриваемого временного интервала в условиях определенной стабильности.
В дальнейшем будет сравнено качество прогнозов классическими методами и методами, основанными на частотном разложении временного ряда, такими как Фурье–продолжение и вейвлет–преобразование, а также будут разработаны и применены дополнительные параметры оценки качества прогноза для других финансовых рынков отличных от Forex.
Вейвлет–анализ позволяет проводить анализ временных рядов в различных временных шкалах. Сам по себе вейвлет-анализ по смыслу аналогичен Фурье–анализу. В обоих случаях речь идет о представлении исследуемого процесса в виде линейной комбинации различных функций, именуемых базисом соответствующего преобразования. Вейвлет–анализ представляет по сравнению со спектральным Фурье–анализом следующий логический шаг: техника выделения окон для анализа с изменяющимся размером. Вейвлет–анализ позволяет использовать длинные интервалы, где необходимо получить точную низкочастотную информацию, и короткие временные интервалы, где необходимо получить высокочастотную информацию.
Список использованной литературы
Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование [Текст] // Успехи физических наук, 2001. – Том 171, №5. – С. 465–501.
Ежов А.А., Шумский С.А. Нейрокомпьютинг и его применения в экономике и бизнесе. – М.: МИФИ, 1998. – 224 с.
Синергетичні та еконофізичні методи дослідження динамічних та структурних характеристик економічних систем.// Дербенцев В.Д., Сердюк О.А., Соловйов В.М., Шарапов О.Д. – Монографія. – Черкаси: Брама–Україна, 2010. – 287 с.
Філєр З. Біржові паніки, кризи та Сонце [Текст] //Энергосбережение, энергетика, энергоаудит, №2 (60), 2009. – С. 49 – 54.
Чабаненко Д. М. Дискретне Фур'є-продовження часових рядiв [Текст] // Системнi технологiї. Регiональний мiжвузiвський збiрник наукових праць. – Днiпропетровськ, 2010. – № 1 (66). – С. 114–121.