Анализ существующих методов классификации информации и их применение в системе GrabTheTrade

М.Г. Титаренко, И.А. Коломойцева Анализ существующих методов классификации информации и их применение в системе GrabTheTrade. Представлен анализ существующих алгоритмов классификации, используемых в современных информационно-поисковых системах. Определены методы классификации, которые могут быть использованы в информационной системе GrabTheTrade.

Классификация является важной частью любой информационно-поисковой системы. На сегодняшний день существует несколько основных подходов к классификации и множество вариантов реализации этих подходов. Не все алгоритмы классификации обеспечивают одинаковый уровень корректности результатов и, обычно, имеют свою область применения. В связи с этим было решено рассмотреть, в рамках данной статьи, подходы, которые используются в современных информационно-поисковых системах. В информационной системе GrabTheTrade, которая работает над сбором и анализом торгово-политической информации, планируется разработка внутренней информационно-поисковой системы, составляющей частью которой является классификация полученных данных.

Целью данной работы является анализ подходов к классификации, рассмотрение принципов применения данных подходов, используемых в современных информационно-поисковых системах, определение возможности их использования в системе GrabTheTrade.

Любая классификация производится на основе каких-либо признаков. Для того чтобы классифицировать текст прежде всего необходимо определить значения выбранных признаков для этого текста. Для использования математических методов признаки, как правило, должны иметь количественное выражение. Количественным выражением признаков, связанных с наличием, взаимодействием или взаиморасположением определенных элементов в тексте, могут стать частоты появления этих элементов (например, частоты появления букво- или словосочетаний). Существуют также и другие виды количественного представления признаков (например, в том случае, когда признак характеризует текст целиком) [1].

Выбор набора количественных признаков играет решающую роль при классификации текстов. Числа появления часто встречаемых слов значительно более информативны в плане классификации текстов по индивидуальному стилю, чем числа абзацев и числа появления предложений, состоящих из определенного числа слов.

Одним из классов методов классификации являются методы, связанные с машинным обучением. При использовании таких подходов возникает возможность оверфиттинга.

Оверфиттинг представляет собой явление, при котором алгоритм машинного обучения настраивается на шум, ошибки и нехарактерные данные в обучающей выборке.

Деревом решений называют представленный в виде ациклического графа план, по которому производится классификация объектов, описанных набором атрибутов, по некоему целевому атрибуту. В задаче классификации текстов объектами являются тексты (фрагменты текстов), целевым атрибутом – класс текстов (стиль, жанр и т.п.). В качестве атрибутов, описывающих текст, будем использовать количественные признаки текста.

Каждый узел дерева содержит условие ветвления по одному из атрибутов.

Следуя по обученному дереву в соответствии со значениями атрибутов произвольного объекта, мы окажемся в одном из листов дерева. Значение этого листа определит значение целевого атрибута (класс) объекта.

При использовании деревьев решений для борьбы с оверфиттингом используют методики прореживания (prunning). При прореживании на основе некоторого критерия отбрасываются те узлы дерева, которые наиболее вероятно настроились на шум и сократили способность дерева к обобщению. В задаче классификации текстов нехарактерные данные и шум – частое явление (например, фрагменты 302 текста, написанные в несколько ином, чем предполагается, стиле), поэтому использовать прореживание необходимо [2].

Узнать эффективность классификации самого метода деревьев решений (без учета информативности признаков), можно лишь сравнив результаты его работы с результатами работы других методов классификации на одних и тех же данных.

Нейронные сети – вид математических моделей, которые строятся по принципу организации сетей нервных клеток мозга. В основе их построения лежит идея о том, что сколь угодно сложные процессы можно моделировать довольно простыми элементами (нейронами), а вся основная функциональность нейронной сети, состоящей из набора нейронов, обеспечивается связями между нейронами.

Существует множество видов нейронных сетей различной структуры. Нейронные сети прямого распространения являются наиболее популярным и хорошо зарекомендовавшим себя на различных задачах видом нейронных сетей. Они позволяют производить нелинейную аппроксимацию произвольной функции (в нашем случае функции принадлежности к классу) по набору примеров. Нейроны в данных сетях объединены в слои. Сеть состоит из произвольного числа слоев. Нейроны каждого слоя соединяются с нейронами предыдущего и последующего слоев по принципу «каждый с каждым» [3].

Однако при этом возникают следующие проблемы:

• сеть обучается слишком медленно;
• величина признака зависит от размера текста, поэтому при обучении и тестировании на текстах различных размеров сеть не сможет найти правильное решение.

На задаче классификации текстов по количественным признакам нейронные сети заметно превосходят по эффективности деревья решений. Но при этом их настройка происходит значительно дольше (в 10 и более раз), чем производится построение деревьев решений, а также перед обучением необходимо дополнительно производить нормализацию данных. Кроме того, деревья решений дают легко интерпретируемый ответ в виде набора правил выбора того или иного класса, а нейронные сети – лишь информацию о степени принадлежности к классам. Поэтому выбор того или иного метода зависит от задачи: если необходима высокая точность классификации текстов, то следует применять нейронные сети, если нужен наглядный и быстрый ответ – деревья решений.

В основе NBC (Naive Bayes Classifier) лежит теорема Байеса.

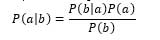
где,

• P(a|b) — вероятность что документ b принадлежит классу a, именно её нам надо рассчитать;
• P(b|a) — вероятность встретить документ b среди всех документов класса a;
• P(a) — безусловная вероятность встретить документ класса a в корпусе документов;
• P(b) — безусловная вероятность документа b в корпусе документов.

Теорема Байеса позволяет переставить местами причину и следствие. Зная, с какой вероятностью причина приводит к некоему событию, эта теорема позволяет расcчитать вероятность того что именно эта причина привела к наблюдаемому событию [4].

Цель классификации состоит в том, чтобы понять к какому классу принадлежит документ, поэтому нужна не сама вероятность, а наиболее вероятный класс. Байесовский классификатор использует оценку апостериорного максимума для определения наиболее вероятного класса.

То есть надо рассчитать вероятность для всех классов и выбрать тот класс, который обладает максимальной вероятностью.

Достоинства метода [5]:

• в модели определяются зависимости между всеми переменными, это позволяет легко обрабатывать ситуации, в которых значения некоторых переменных неизвестны;
• байесовские сети достаточно просто интерпретируются и позволяют на этапе прогностического моделирования легко проводить анализ по сценарию "что, если";
• байесовский метод позволяет естественным образом совмещать закономерности, выведенные из данных, и, например, экспертные знания, полученные в явном виде;
• использование байесовских сетей позволяет избежать проблемы оверфиттинга.

Недостатки метода:

• на результат классификации в наивно-байесовском подходе влияют только индивидуальные значения входных переменных, комбинированное влияние пар или троек значений разных атрибутов здесь не учитывается. Это могло бы улучшить качество классификационной модели с точки зрения ее прогнозирующей точности, однако, увеличило бы количество проверяемых вариантов.

Машина опорных векторов (SVM) принимает набор данных, состоящий из чисел, и пытается спрогнозировать, в какую категорию он попадает. Можно, например, определить роль игрока в футбольной команде по его росту и скорости бега. Для простоты рассмотрим всего две возможности: позиция в защите, для которой требуется высокий рост, и в нападении, где игрок должен быстро перемещаться [6].

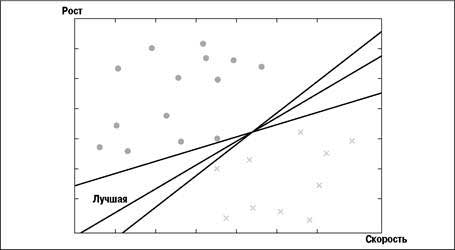
SVM строит прогностическую модель, отыскивая линию, разделяющую две категории. Если отложить по одной оси рост, а по другой – скорость и нанести наилучшие позиции для каждого игрока, то получится диаграмма, изображенная на рисунке. Защитники представлены крестиками, а нападающие – кружками. Также на диаграмме показано несколько линий, разделяющих данные на две категории.

Машина опорных векторов находит линию, наилучшим образом разделяющую данные. Это означает, что она проходит на максимальном расстоянии от расположенных вблизи нее точек. На рисунке разделяющих линий несколько, но наилучшая из них помечена надписью «Лучшая». Для определения того, где должна пройти линия, необходимы лишь ближайшие к ней точки, они и называются опорными векторами.

После того как разделяющая линия найдена, для классификации новых образцов требуется лишь нанести их на диаграмму и посмотреть, по какую сторону от разделителя они окажутся. Просматривать обучающие данные при классификации новых образцов ни к чему, поэтому классификация производится очень быстро.

Недостаток заключается в том, что оптимальная функция и ее параметры зависят от конкретного набора данных, так что всякий раз приходится подбирать их заново.

Данный метод более приспособлен к большим объемам данных, тогда как деревья решений дают информацию уже на небольшом наборе данных. Также, как и нейронные сети, представляет собой «черный ящик».

Метод ближайших соседей (k Nearest Neighbors, или kNN) — очень популярный метод классификации. Это один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей, какие преобладают, таков и ты. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных [7].

Согласно методу ближайших соседей, тестовый пример (шарик) будет отнесен к классу треугольники, а не квадраты.

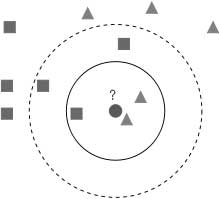
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции [8]:

• вычислить расстояние до каждого из объектов обучающей выборки;
• отобрать k объектов обучающей выборки, расстояние до которых минимально;
• класс классифицируемого объекта — это класс, наиболее часто встречающийся среди k ближайших соседей.

Для классификации текста в данном методе в качестве объектов выбираются слова, предложения и абзацы, которые уже определены в данном тексте. Так, если первый и третий абзацы текста имеют экономический стиль, то скорее всего и второй абзац также относится данному стилю.

Для метода ближайших соседей существуют теоремы, утверждающие, что на "бесконечных" выборках это оптимальный метод классификации. Это одновременно является как плюсом, так как корректность классификации при этом является достаточно высокой, так и минусом данного метода, в связи с необходимостью иметь большие выборки данных.

Был проведен анализ существующих алгоритмов классификации, были рассмотрены методы получения достоверной информации в информационно-поисковых системах.

Информационная система «GrabTheTrade» — это система сбора, анализа и наглядного вывода торгово-экономической информации. Она обеспечивает получение данных с заданных интернет источников, анализ достоверности полученных данных, агрегацию и ежеквартальное автоматическое обновление данных.

В системе планируется реализация информационно-поисковой системы для получения торгово-политической информации. После осуществления поиска и ранжирования информации в системе будет проводится классификация полученных данных. Для проведения классификации в данной системе можно использовать методы, которые требуют большой объем данных, а именно нейронные сети, SVM. Также возможно использование комбинации различных методов для разных этапов классификации, а также оптимизации корректности полученных данных.