A STUDY OF VARIOUS STANDARDS FOR TEXT COMPRESSION TECHNIQUES
Authors: Singh M., Singh N.
Source: Singh M., Singh N. A study of various standards for text compression techniques
Abstract
This paper compares different Text compression algorithms of text files: Huffman, Shannon-Fano, Arithmetic, LZ, LZW algorithm techniques. There are three types of text that are processed by a multimedia computer and these are: Unformatted text, formatted text and hypertext. Texts are captured from the keyboard and hypertext can be followed by a keyboard, mouse and some other devices when it being run on a computer. The original words in a text file are transformed into codewords having length 2 and 3. The most frequently used words use 2 length codewords and the rest use 3 length codewords for better compression. The codewords are chosen in such way that the spaces between words in the original text file can be removed altogether recovering a substantial amount of space.
Keywords: Data compression, Text Compression, Huffman Coding, Shannon-Fano Coding, Arithmetic Coding, LZ Coding, LZW.
I. INTRODUCTION
Text is a very big part of most files that digital technology users create. For example, these files could be: Word or PDF documents, emails, cellphone texts (SMS format) or web pages. The large capacity of storage devices that are currently available; Text compression has important applications in the areas of data transmission and data storage because it require efficient ways to store and transmit different types of data such as text, image, audio, and video, and hence reduce execution time and memory size [1]. The general principle of Text compression algorithms on text files is to transform a string of characters into a new string that contains the same information but where the transformed string is considerably reduced as measured by scales such as: compression size, compression ratio, processing time/speed and entropy.
II. COMPRESSION TECHNIQUE
Compression technique is used to reduce the volume of information to be stored into storages or to reduce the communication bandwidth required for its transmission over the networks. Compression is used for different types of data, Example: documents, sound, video. It is either applied to transfer a file, whether on a disk or over a network, to ensure that the file can fit on the storage device, or both. The aim of compression is reduce the quantity of the file size but to keep the quality of the original data.
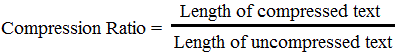
Compression technique can be divided into two categories: a) Lossless Compression, b) Lossy Compression.
a) Lossless Compression
Lossless compression algorithm the aim is to reduce the amount of source Information to be transmitted in such a way that, when the compressed information is decompressed, there is no loss of information. Lossless compression is said therefore, to be reversible [2]. In simple words, first Compressed then Decompressed data is an exact replication. Lossless compression is used in many applications. For example, it is used in WinZip, General Purpose (HTTP, ASCII, and Morse code), Media (TIFF, PNG, FLAC, MPEG-4 (ALS) and GIF), Very few video codecs are lossless.
b) Lossy Compression
The aim of lossy compression algorithm is normally not to reproduce an exact copy of the source information after decomposition but rather a version of its which is perceived by the recipient as a true copy (approx) [2]. In simple words, there is some distortion between original and reproduced. Lossless compression is used in many applications. For example, it is used in Images (JPEG), Videos (MPEG), and Audio (MP3).
III. COMPRESSION ALGORITHMS
Compression techniques are well-suited for Text Retrieval systems: a) It achieve good compression ratio, b) It maintain good search capabilities and c) It permits direct access to the compressed text.
A. Huffman Coding
Huffman algorithm is the oldest and most widespread technique for data compression. It was developed by David A. Huffman in 1952 and used in compression of many type of data such as text, image, audio, and video. It is based on building a full binary tree bottom up for the different symbols that are in the original file after calculating the frequency/probability for each symbol and put them in descending order. After that, it derive the codewords for each symbol from the binary tree, giving short code words for symbols with large probabilities and longer code words for symbols with small probabilities. Huffman algorithm assigns every symbol to a leaf node, Root node and Branch node of a binary code tree. The tree structure results from combining the nodes step-by-step until all of them are embedded in a root tree. The algorithm always combines the two nodes providing the lowest frequency in a bottom up procedure. The new interior nodes gets the sum of frequencies of both child nodes. This is known as Huffman code tree.
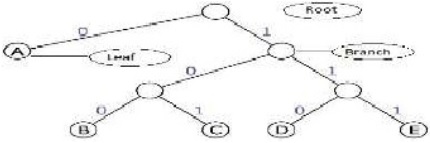
Fig. 1. Huffman Tree
The branches of the tree represent the binary values 0 and 1 according to the rules for common prefix-free code trees. The path from the root tree to the corresponding leaf node defines the particular code word.
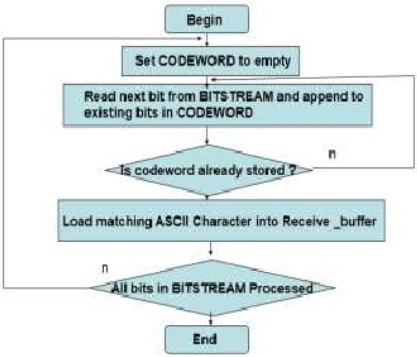
Flowchart 1. Algorithm of Huffman coding
Huffman Encoding is of two types:
a. Static Huffman Coding
b. Dynamic Huffman Coding
a. Static Huffman Coding
- Static Huffman coding assigns variable length codes to symbols based on their frequency of occurrences in the given message. Low frequency symbols are encoded using many bits, and high requency symbols are encoded using fewer bits.
- The message to be transmitted is first analyzed to find the relative frequencies of its constituent characters.
- The coding process generates a binary tree, the Huffman code tree, with branches labeled with bits (0 and 1).
- The Huffman tree (or the character codeword pairs) must be sent with the compressed information to enable the receiver decode the message.
b. Dynamic Huffman Coding
- In this method encoder and decoder build the Huffman tree , hence the codeword table dynamically.
- If the character to be transmitted is currently present in the tree its codeword is determined and sent in the normal way.
- If the character is not present then it is transmitted in its uncompressed form.
- Encoder updates Huffman tree either by increasing the frequency of the occurrence or introducing a new character.
- Transmitted codeword is encoded in such a way that the receiver will be able to determine the character being received and also carry out some modifications to its own copy of the tree for new updated tree structure.
B. Shannon-Fano Coding
At about 1960 Claude E. Shannon (MIT) and Robert M. Fano (Bell Laboratories) had developed a coding procedure to generate a binary code tree. The procedure evaluates the symbol's probability and assigns code words with a corresponding code length. Compared to other methods the Shannon-Fano coding is easy to implement. In practical operation Shannon-Fano coding is not of larger importance. This is especially caused by the lower code efficiency in comparison to Huffman coding as demonstrated later. Utilization of Shannon-Fano coding makes primarily sense if it is desired to apply a simple algorithm with high performance and minimum requirements for programming. An example is the compression method IMPLODE as specified e.g. in the ZIP format.
C. Arithmetic Coding
In Arithmetic coding optimal compression ratio for a data source is traditionally described with respect to Claude Shannon’s [6] definition of source entropy [5]; a measure of the source’s information and therefore the average number of bits required to represent it. In arithmetic coding, a message is encoded as a real number in an interval from one to zero. Arithmetic coding typically has a better compression ratio than Huffman coding, as it produces a single symbol rather than several separate codewords. Arithmetic coding is a lossless coding technique.
D. Lempel-Ziv Coding (LZ)
A variety of compression methods is based on the fundamental work of Abraham Lempel and Jacob Ziv. The LZ family, including LZ77, LZ78, LZW, and their variants (Welch 1984, Ziv and Lempel 1977, Ziv and Lempel 1978) are the most popular dictionary-based compression algorithms because of their speed and good compression ratio.
E. Lempel-Ziv-Welsh (LZW)
In 1977, Abraham Lempel and JakobZiv created the first, now the days this compression technique is called the LZ family of substitution compressors. In 1984, while working for Unisys, Terry Welch modified the LZ78 compressor for implementation in high-performance disk controllers. Ziv and Lempel [7] have proposed a coding technique which involves the adaptive matching of variable length strings. The result was the LZW algorithm that is commonly found today. It is a general compression algorithm capable of working on almost any type of data, creating a table of strings commonly occurring in the data being compressed and replacing the actual data [3]. The original Lempel-Ziv approach to data compression was first published in 1977[4]. Terry Welch's refinements to the algorithm were published in 1984[4]. The algorithm is surprisingly simple. In a nutshell, LZW compression replaces strings of characters with single codes. It does not do any analysis of the incoming text; it just adds every new string of characters it sees to a table of strings. Compression occurs when a single code is output instead of a string of characters [4]. A "dictionary" of all the single character with indexes 0...255, is formed during encoding/compression starts and is used in decoding/de-compression. Codes 0-255 refer to individual bytes, while codes 256-4095 refer to substrings [4].
TABLE I. Different Compression methods and their Techniques
| Method | Compression (% of input) | Encoding (MB/min) | Decoding (MB/min) | Techniques Used |
| lzrw1 | 63.5 | 70 | 190 | LZ77 method, adaptive, tuned for speed [8] |
| pack | 61.8 | 60 | 30 | Zero-order character-based, semi-static, Huffman coding |
| cacm | 61.2 | 6 | 5 | Zero-order character-based, semi-static, adaptive, arithmetic coding[9] |
| compress | 43.2 | 25 | 55 | LZ78 implementation, adaptive [10] |
| gzip-f | 38.6 | 15 | 95 | LZ77 method, adaptive, fast option |
| gzip-b | 36.8 | 8 | 100 | LZ77 method, adaptive, best option |
| dmc | 28.7 | 1 | 1 | Variable-order bit-based, adaptive, arithmetic coding [11] |
| huffword | 28.4 | 10 | 65 | Zero-order word-based, semi-static, Huffman coding [12] |
| ppmc | 24.1 | 4 | 4 | Fifth-order character-based, adaptive, arithmetic coding [13] |
IV. DIFFERENT STANDARD SCALES OF COMPRESSION MEASUREMENT
- Compression size: The size of the new file in bits after compression is complete.
- Compression ratio: The ratio of the compression size in to the original file size expressed as a percentage.
- Processing time or speed in millisecond: The ratio of the time required for compressing the whole file to the number of symbols in the original file expressed as symbol/ millisecond.
- Entropy: The ratio of the compression size to the number of symbols in the original file expressed as bits/symbol.
V. CONCLUSION
Compression is an important technique in the multimedia computing field. This is because it can reduce the size of the data and transmitting and storing the reduced data on the Internet and storage devices are faster and cheaper than uncompressed data. In other words, these algorithms are important parts of the multimedia data compression standards. Texts are always compressed with lossless compression algorithms. This is because a loss in a text will change its original concept. Repeated data is important in text compression. If a text has many repeated data, it can be compressed to a high ratio. This is due to the fact that compression algorithms generally eliminate repeated data. For such as real-time applications, Huffman algorithm can be used.
REFERENCES
- Elabdalla, A. R. and Irshid, M. I.,”An efficient bitwise Huffman coding technique based on source mapping”. Computer and Electrical Engineering 27 (2001) 265 – 272.
- Multimedia Communications: Applications, Networks, Protocols and Standards by Fred Halsall.
- Michael Heggeseth, Compression Algorithms: Huffman and LZW, CS 372: Data Structures, December 15, 2003.
- Mark Nelson, LZW Data Compression, Dr. Dobb'sJournal, October 1989.
- I.Witten, R. Neal, and J. Cleary, “Arithmetic coding for data compression,” Communications of the ACM, vol. 30, no. 6, pp. 520 – 540, June 1987.
- C. E. Shannon, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, pp. 379-423 and 623-656, July and October, 1948.
- J Ziv and A. Lempel, “Compression of individual sequences via variable-rate coding,” IEEE Trans. Inform. Theory, vol. IT-24, pp. 530-536, Sept. 1978.
- R.N. Williams. An extremely fast Ziv-Lempel data compression algorithm. In J.A. Storer and J.H. Reif, editors, Proc. IEEE Data Compression Conference, pages 362-371, Snowbird, Utah, April 1991. IEEE Computer Society Press, Los Alamitos, California.
- I.H. Witten, R. Neal, and J.G. Cleary. Arithmetic coding for data compression. Communications of the ACM, 30(6):520-541, June 1987.
- T.A. Welch. A technique for high performance data compression. IEEE Computer, 17:8-20, June 1984.
- G.V. Cormack and R.N. Horspool, Data compression using dynamic Markov modeling, The Computer Journal, 30(6):541-550, December 1987.
- A. Mo_at and J. Zobel. Coding for compression in full-text retrieval systems. In J.A. Storer and M. Cohn, editors, Proc. IEEE Data Compression Conference, pages 72-81, Snowbird, Utah, March 1992. IEEE Computer Society Press, Los Alamitos, California.
- J.G. Cleary and I.H. Witten. Data compression using adaptive coding and partial string matching. IEEE Transactions on Communications, COM-32:396-402, April 1984.