Data Compression Considering Text Files
Authors: Sailunaz K., Alam Kotwal M., Nurul Huda M.
Source: International Journal of Computer Applications (0975 – 8887) Volume 90 – No 11, March 2014
Abstract
Lossless text data compression is an important field as it significantly reduces storage requirement and communication cost. In this work, the focus is directed mainly to different file compression coding techniques and comparisons between them. Some memory efficient encoding schemes are analyzed and implemented in this work. They are: Shannon Fano Coding, Huffman Coding, Repeated Huffman Coding and Run-Length coding. A new algorithm “Modified Run-Length Coding” is also proposed and compared with the other algorithms. These analyses show how these coding techniques work, how much compression is possible for these coding techniques, the amount of memory needed for each technique, comparison between these techniques to find out which technique is better in what conditions. It is observed from the experiments that the repeated Huffman Coding shows higher compression ratio. Besides, the proposed Modified run length coding shows a higher performance than the conventional one.
General Terms: Information Theory, Algorithms.
Keywords: Data compression, Lossless compression, Encoding, Compression Ratio, Code length, Standard deviation.
1. INTRODUCTION
In computer science and information theory, text compression is the process of encoding texts using fewer bits or symbols than an original representation, by using specific encoding techniques. Text data compression is useful because it helps to reduce the consumption of expensive resources, such as hard disk space or transmission bandwidth. But the problem is that the decompression must be needed for further utilization and this extra processing may be unfavorable to some applications. The objectives of this work are efficient representation and implementation of some text data compression algorithm, proposing a new compression method named “Modified Run-Length Coding”, computation of some important compression factors for each of these algorithms, comparison between different encoding techniques, and improvement of performance of different data compression techniques and selecting a suitable encoding technique for real life system.
This paper is organized as follows: Section 2 discusses the related works for data compression. Section 3 explains the different algorithms of data compression techniques. Section 3 also analyzes the experimental results with proper reasons. Section 4 concludes the paper with some future remarks.
2. RELATED WORKS
In 1949, C. Shannon and R. Fano devised a systematic way to assign code words based on probabilities of blocks called the Shannon Fano Coding. An optimal method for this was found by D. Huffman in 1951 which is known as the Huffman Algorithm [1]. Huffman Algorithm is being used for compression since then.
A research in [7] showed that text data compression using Shannon Fano algorithm has a same effectiveness with Huffman algorithm when all character in string are repeated and when the statement is short and just one character in the statement is repeated, but the Shannon Fano algorithm is more effective than Huffman algorithm when the data has a long statement and data text have more combination character in statement or in string or word. A variety of data compression methods spanning almost forty years of research, from the work of Shannon, Fano and Huffman in the late 40’s to a technique developed in 1986 was surveyed in [10]. The compression ratio, compression time and decompression time for the Run Length Encoding (RLE) Algorithm, Huffman Encoding Algorithm, Shannon Fano Algorithm, Adaptive Huffman Encoding Algorithm, Arithmetic Encoding Algorithm and Lempel Zev Welch (LZW) Algorithm using random text files were compared in [2]. It showed that, the compression time increased as file size increased. For Run Length encoding it was a constant value and not affected by the file size. Compression times were average values for two Static Huffman approaches, and times of Shannon Fano approach were smaller than the other algorithm. The LZW Algorithm worked well for only small files. Compression times of Adaptive Huffman algorithm were the highest. Decompression times of all the algorithms were less than 500000 milliseconds except the Adaptive Huffman Algorithm and LZW. The compression ratio were similar except the Run Length coding and for small sized files, LZW gave the best results.
The comparison between RLE, Huffman, Arithmetic Encoding, LZ-77, LZW and LZH (first LZ applied, then Huffman) on random .doc, .txt, .bmp, .tif, .gif, and .jpg files is shown in [3]. It showed that, LZW and Huffman gave nearly same results when used for compressing text files. Using LZH compression to compress a text file gave an improved compression ratio than the others. Different methods of data compression algorithms such as: LZW, Huffman, Fixed-length code (FLC), and Huffman after using Fixed-length code (HFLC) on English text files were studied in [12] in terms of compression Size, Ratio, Time (Speed), and Entropy. LZW was the best algorithm in all of the compression scales, then Huffman, Huffman after using Fixed length code (HFLC), and Fixed-length code (FLC), with entropy 4.719, 4.855, 5.014, and 6.889 respectively. A similar work is found in [12] which analyzed Huffman algorithm and compared it with other common compression techniques like Arithmetic, LZW and Run Length Encoding on the basis of their use in different applications and their advantages and concluded that arithmetic coding is very efficient for more frequently occurring sequences of pixels with fewer bits and reduces the file size dramatically. RLE is simple to implement and fast to execute. LZW algorithm is better to use for TIFF, GIF and Textual Files and is easy to implement, fast and lossless algorithm whereas Huffman algorithm is used in JPEG compression which produces optimal and compact code but relatively slow.
Shannon Fano coding, Huffman coding, Adaptive Huffman coding, RLE, Arithmetic coding, LZ77, LZ78 and LZW were tested using the Calgary corpus in [4]. In the Statistical compression techniques, Arithmetic coding technique outperformed the rest with some identifiable improvements. LZB outperformed LZ77, LZSS and LZH to show a marked compression. LZ78 and LZW were outperformed in their average BPC by LZFG. The entropy was calculated in [8] on the same English text file for Shanon Fano coding, Huffman Encoding, Run- Length Encoding (RLE), Lempel-Ziv-Welch (LZW). The compression ratio was almost same for the Shannon Fano and Huffman coding and 54.7% space could be saved by those two algorithms. The compression ratio of Run length encoding and Lempel-Ziv-Welch algorithms was low as compared with the Huffman and Shannon Fano algorithms and it concluded that, Huffman encoding algorithm is the best result for the text files. Another comparison based work was [13] which discussed Run Length based codes like Golomb code, Frequency Directed run length code (FDR), Extended FDR, Modified FDR, Shifted Alternate FDR, and OLEL coding methodology; Huffman coding; Shannon Fano coding; Lempel-Ziv-Welch coding; Arithmetic coding; Universal coding like Elias Gamma code, Elias Delta code, Elias Omega code and proposed double compression using Huffman code technique to reduce the test data volume and area even further. First, the data was compressed by any one of the run length based codes like Golomb code, FDR code, EFDR, MFDR, SAFDR, and OLEL coding and then from the compressed data, another compression was made by Huffman code. Double compression using Huffman code had compression ratio of 50.8%. Better results were achieved for the data sets with redundant data.
The execution times, compression ratio and efficiency of compression methods in a client-server distributed environment using four compression algorithms: Huffman algorithm, Shannon Fano algorithm, Lempel-Ziv algorithm and Run-Length Encoding algorithm were analyzed in [9]. The data from a client was distributed to multiple processors/servers, subsequently compressed by the servers at remote locations, and sent back to the client. Simgrid Framework was used and results showed that the LZ algorithm attains better efficiency/scalability and compression ratio but it worked slower than other algorithms. Huffman coding, LZW coding, LZW based Huffman coding and Huffman based LZW were compared for multiple and single compression in [6]. It showed that Huffman based LZW Encoding can Compresses data more than all other three cases, when in average case the Huffman based LZW compression ratio is 4.41, where other maximum average compression ratio is 4.17 in case of LZW compression. The Huffman based LZW compression is better in some of the cases than LZW Compression.
3. EXPERIMENTAL SETUP AND ANALYSIS
In this work, some existing data compression algorithms [5] are implemented and a new algorithm named modified run length coding using a new idea is introduced. All of these algorithms are also tested using the text files (alice29.txt, asyoulik.txt, lcet10.txt, plrabn12.txt) of the Canterbury corpus.
The computation of the compression ratio, average code length and standard deviation for all the existing and new approach and analysis of the results gives some ideas about the performances of these algorithms with text files with different contents and sizes.
3.1 Existing Algorithms
At first, the existing algorithms (Run-Length Coding, Shannon Fano Coding, Huffman Coding and Repeated Huffman Coding) are explained which are also been implemented.
3.1.1 Run-Length Coding
Set Count = 0
Read two consecutive symbols from input file.
Current_Symbol = first symbol
Next_Symbol = second symbol
If Current_Symbol matches Next_Symbol
Increase the value of Count by 1
Make
Current_Symbol = Next_Symbol
Next_Symbol = read next
symbol from input file
Repeat
Else
Write the value of Count
Write the value of Current_Symbol
Set Count = 0
Repeat
Show the compressed data
3.1.2 Shannon Fano Coding
Read the input file
Compute the frequencies for each used symbol
Sort the lists of symbols according to frequency
Place the most frequently occurring symbols at the left and the least common at the right
Divide the list into two parts
With the total frequency counts of the left half being as close to the total of the right as possible
Assign 0 to the left half of the list
Assign 1 to the right half of the list
Recursively repeat this for each of the two halves until each symbol has become a corresponding code leaf on the tree.
Generate the codeword for each symbol
Create a file by replacing each symbol of the input file with their respective codewords
Take a set of eight digits from that file
Convert into decimal value
Convert the decimal value into a single symbol
Write that symbol in output file
Repeat for all the symbols of input file
3.1.3 Huffman Coding
Compute the frequencies for each used symbol
Sort the list in ascending order
Extract first two lowest frequencies
Create a node as the parent of them
Assign the new node a frequency equal to the sum of its children’s frequencies
Insert the new node into the list
Sort it again
Repeat until there is only one parentless node left
Now the Huffman Tree is generated
Assign 0 for the left child of each node
Assign 1 for the right child of each node
Generate the codeword for each symbol
Create a file by replacing each symbol of the input file with their respective codewords
Take a set of eight digits from that file
Convert into decimal value
Convert the decimal value into a single symbol
Write that symbol in output file
Repeat for all the symbols of input file
3.1.4 Repeated Huffman Coding
Take an input text file
Implement the Huffman algorithm on the input file
Obtain the compressed output file
If the size of the output file is less than the size of the input file then
Take this output file as the new input
Repeat the process.
Else
Stop compressing
Show the final compressed file as output.
3.2 A New Approach: Modified Runlength Coding Algorithm
A new approach by mixing up the Huffman Coding and Run-Length coding is tried to see if a more compressed output is possible or not. It is called the “Modified Runlength Coding”. The algorithm is as follows:
Compute the frequencies for each used symbol
Sort the list in ascending order
Extract first two lowest frequencies
Create a node as the parent of them
Assign the new node a frequency equal to the sum of its children’s frequencies
Insert the new node into the list
Sort it again
Repeat until there is only one parentless node left
Now the Huffman Tree is generated
Assign 0 for the left child of each node
Assign 1 for the right child of each node
Generate the codeword for each symbol
Create a file by replacing each symbol of the input file with their respective codewords
Set Count = 0
Read two consecutive symbols from the file.
Current_Symbol = first symbol
Next_Symbol = second symbol
If Current_Symbol matches Next_Symbol
Increase the value of Count by 1
Make
Current_Symbol=Next_Symbol
Next_Symbol = read next symbol from the file
Repeat trying to match symbols
Else
Write the value of Count
Write the value of Current_Symbol
Set Count = 0
Repeat trying to match symbols
Replace
10 by ‘a’,
11 by ‘A’,
20 by ‘b’,
21 by ‘B’,
30 by ‘c’,
31 by ‘C’ and so on.
Show the final compressed file.
3.3 Equations
For each input file, the compression ratio, average code length and standard deviation are computed using each of the different data compression algorithms. The formulae used for the calculations are:
Compression Ratio = Compressed File / Original File
Average Code Length, μ = ΣCode Length / n
Standard Deviation, σ = Σ(Code Length - μ)2 / n
Where n = total number of symbols used in the input file.
3.4 Results
Table 1 shows the comparison with respect to the compression ratio, average code length and standard deviation between five different data compression techniques.
The compression ratio depends on the output file size. The more compressed the output file, the less the compression ratio is. When the compression ratio exceeds 1, the output file size is larger than the original input file size. Here, we can see that, for most of the input files, the Runlength coding and the Modified Runlength coding have compression ratio greater than 1, which means, these algorithms expands the original files instead of compressing them. The Runlength coding works better for files with consecutive repetitions of symbols, but normally data files does not have much consecutive repetitions. That is why the compression ratio is greater than 1. The same idea is also applicable for Modified Runlength coding. The table also shows that, Shannon Fano coding gives better compression for most inputs than Huffman coding, because, for some input files, the code lengths of symbols in Huffman coding become so large that it expands the output files than the original input files. We can say form the table that, the Repeated Huffman coding gives the best compression ratios for most of the files.
The algorithms occupy less memory if the code lengths are smaller. Now, if we consider the average code length, we will see that, for Runlength coding, we do not have any value for average code length because, no codewords are generated in Runlength coding. But, for other techniques, Shannon Fano has smaller code length than Huffman coding and Modified Runlength coding. Here also, the Repeated Huffman coding gives the best average code length for most of the files.
Again, the algorithms occupy less memory if the standard deviations are smaller. Here also, for Runlength coding, we do not have any value for standard deviation because, no codewords are generated in Runlength coding. But, for other techniques, Shannon Fano has smaller standard deviation than Huffman coding and Modified Runlength coding. Again, the Repeated Huffman coding gives the best standard deviation for most of the files.
Table 1. Comparison between different data compression techniques
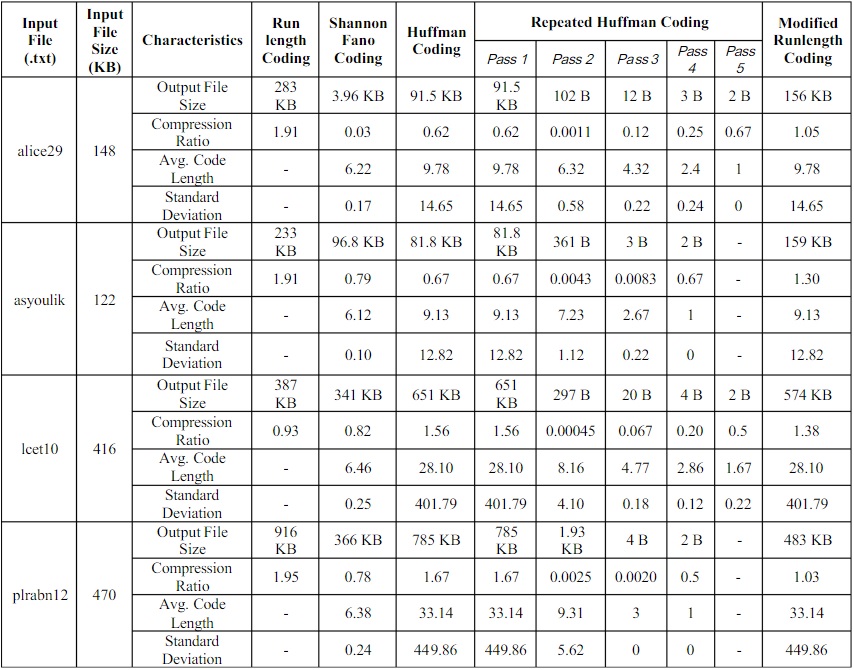
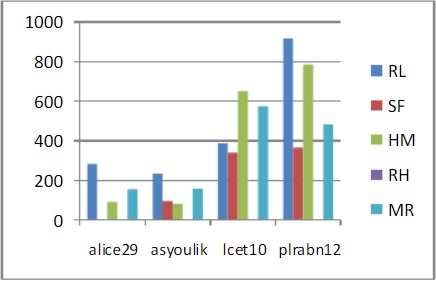
Fig 1: Comparison based on Output File Size
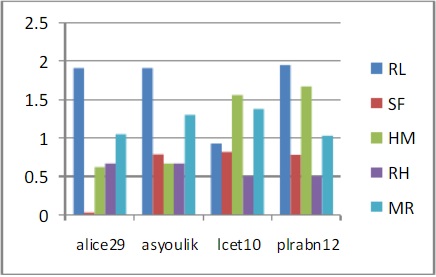
Fig 2: Comparison based on Compression Ratio
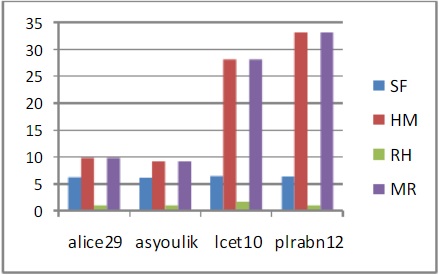
Fig 3: Comparison based on Average Code Length
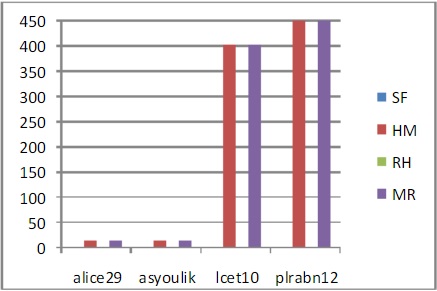
Fig 4: Comparison based on Standard Deviation
Fig 1, Fig 2, Fig 3 and Fig 4 show the comparisons between different algorithms based on output file size, compression ratio, average codelength and standard deviation respectively for Shannon Fano Coding (SF), Huffman Coding (HM), Repeated Huffman Coding (RH), Run-Length Coding (RL) and Modified Run-Length Coding (MR) using the input text files alice29.txt, asyoulik.txt, lcet10.txt and plrabn12.txt. In all these Figures, the output file size, compression ratio, average codelength and standard deviation of Repeated Huffman coding is taken from the final pass of the algorithm. In Fig. 1, it can be seen that the output file sizes of Shannon Fano and Repeated Huffman are much less than the other algorithms and a similar situation can be seen for the standard deviations of these two algorithms in Fig. 4.
From the above analysis, it can be said that the Repeated Huffman coding has the best results for most of the cases. It has smaller compression ratio, average code length and standard deviation. So, it seems the best algorithm among them. But, it should also be considered that, for the best results, it had to run through up to five passes of the algorithm. It ultimately results in occupying less memory than others for the output file after the final pass, but it has to go through several passes for that, indicating more running time than the others, which is a problem in many cases. It also occupies more memory for the first several passes.
If the extra running time for Repeated Huffman coding is considered, then Shannon Fano coding gives a quite good result in less running time. The Runlength coding can be very effective for files with consecutive repetitions. The Modified Runlength coding can be very useful if the intermediate temporary file, which can be generated after applying the Huffman coding on the input file, have consecutive 0 and 1 repetitions.
Finally, it is clear that, each data compression technique has its pros and cons. It depends on the content of the input files that how much better compressions can be achieved.
4. CONCLUSION
After computing and comparing the compression ratio, average code length and standard deviation for Shannon Fano Coding, Huffman Coding, Repeated Huffman Coding, Run-Length Coding and Modified Run-Length Coding, an idea is generated about how much compression can be obtained by each technique. So, now the most effective algorithm can be used based on the input text file size, content type, available memory and execution time to get the best result. A new approach for data compression “Modified Run Length algorithm” is also proposed here and which gives a lot better compression than the existing Run-Length algorithm. Future works can be carried on an efficient and optimal coding technique using mixture of two or more coding techniques for image file, exe file etc. to improve compression ratio and reduce average code length.
5. REFERENCES
- M. N. Huda, “Study on Huffman Coding,” Graduate Thesis, 2004.
- S.R. Kodituwakku and U. S. Amarasinghe, “Comparison of Lossless Data Compression Algorithms for Text Data,” Indian Journal of Computer Science and Engineering, vol. I(4), 2007, pp. 416-426.
- M. Al-laham and I. M. M. E. Emary, “Comparative Study between Various Algorithms of Data Compression Techniques,” International Journal of Computer Science and Network Security, vol.7(4), April 2007, pp. 281-291.
- S. Shanmugasundaram and R. Lourdusamy, “A Comparative Study of Text Compression Algorithms,” International Journal of Wisdom Based Computing, vol. I (3), December 2011, pp. 68 – 76.
- K. Sayood, “Introduction to Data Compression,” 4th ed., Elsevier, 2012.
- M. R. Hasan, M. I. Ibrahimy, S. M. A. Motakabber, M. M. Ferdaus and M. N. H. Khan, “Comparative data compression techniques and multicompression results,” IOP Conference, 2013.
- C. Lamorahan, B. Pinontoan and N. Nainggolan, “Data Compression Using Shannon-Fano Algorithm,” JdC, Vol. 2, No. 2, September, 2013, pp. 10-17.
- P. Yellamma and N. Challa, “Performance Analysis of Different Data Compression Techniques On Text File,” International Journal of Engineering Research & Technology (IJERT), Vol. 1 Issue 8, October – 2012.
- M. A. Khan, “Evaluation of Basic Data Compression Algorithms in a Distributed Environment,” Journal of Basic & Applied Sciences, Vol. 8, 2012, pp. 362-365.
- D. A. Lelewer and D. S. Hirschberg, “Data Compression,” Journal - ACM Computing Surveys (CSUR), Vol. 19 Issue 3, September 1987, pp. 261-296.
- M. Sharma, “Compression Using Huffman Coding,” International Journal of Computer Science and Network Security, Vol.10 No.5, May 2010, pp. 133-141.
- H. Altarawneh and M. Altarawneh, “Data Compression Techniques on Text Files: A Comparison Study,” International Journal of Computer Applications (0975 – 8887) , Vol. 26 No.5, July 2011.
- R. S. Aarthi, D. Muralidharan and P. Swaminathan,“Double Compression of Test Data Using Huffman Code,” Journal of Theoretical and Applied Information Technology, Vol. 39 No.2, 15 May 2012, pp. 104-113.